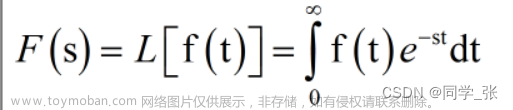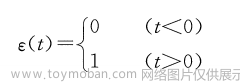0. 前言
谱图使用标准化拉普拉斯矩阵 L n o r m L^{norm} Lnorm 的一个重要原因就是, L n o r m L^{norm} Lnorm 比拉普拉斯矩阵 L L L 稳定。很多资料只是简单地介绍了 L n o r m L^{norm} Lnorm ,在kipfGCN中也只是简单地提到 L n o r m L^{norm} Lnorm 的特征值不大于2。本文搜集了相关lecture,并推导部分内容,来证明这个结论。
1. 正文
设标准化邻接矩阵 A n o r m A^{norm} Anorm 的特征值为 α 1 ≤ α 2 ≤ ⋯ ≤ α n \alpha_1\le\alpha_2\le\cdots\le\alpha_n α1≤α2≤⋯≤αn;标准化拉普拉斯矩阵 L n o r m L^{norm} Lnorm 的特征值为 λ 1 ≤ λ 2 ≤ ⋯ ≤ λ n \lambda_1\le\lambda_2\le\cdots\le\lambda_n λ1≤λ2≤⋯≤λn。有:
− 1 ≤ α 1 ≤ α 2 ≤ ⋯ ≤ α n ≤ 1 -1\le\alpha_1\le\alpha_2\le\cdots\le\alpha_n\le1 −1≤α1≤α2≤⋯≤αn≤1 0 ≤ λ 1 ≤ λ 2 ≤ ⋯ ≤ λ n ≤ 2 0\le\lambda_1\le\lambda_2\le\cdots\le\lambda_n\le2 0≤λ1≤λ2≤⋯≤λn≤2
| 编号 | 推论 | 目的 |
|---|---|---|
| 1.1 | 标准化拉普拉斯是非满秩矩阵 | 标准化拉普拉斯矩阵至少有一个特征值为0 |
| 1.2 | 标准化拉普拉斯矩阵是半正定矩阵 | 标准化拉普拉斯矩阵所有特征值非负 |
1.1 标准化拉普拉斯是非满秩矩阵
1.1.1 拉普拉斯是非满秩矩阵
首先,证明拉普拉斯矩阵 L L L 是非满秩矩阵:
令 D = [ d 1 d 2 ⋱ d n ] D = \begin{bmatrix} d_1 & & & \\ & d_2 & & \\ & & \ddots & \\ & & & dn \\ \end{bmatrix} D= d1d2⋱dn , A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} A= a11a21⋮an1a12a22⋮an2⋯⋯⋯a1na2n⋮ann ,则:
∣
L
∣
=
∣
D
−
A
∣
=
∣
d
1
−
a
11
−
a
12
⋯
−
a
1
n
−
a
21
d
2
−
a
22
⋯
−
a
2
n
⋮
⋮
⋮
−
a
n
1
−
a
n
2
⋯
d
−
a
n
n
∣
(1)
\begin{aligned}\tag{1} |L|=|D-A|=\begin{vmatrix} d_1-a_{11} & -a_{12} & \cdots & -a_{1n} \\ -a_{21} & d_2-a_{22} & \cdots & -a_{2n} \\ \vdots & \vdots & & \vdots \\ -a_{n1} & -a_{n2} & \cdots & d-a_{nn} \\ \end{vmatrix} \end{aligned}
∣L∣=∣D−A∣=
d1−a11−a21⋮−an1−a12d2−a22⋮−an2⋯⋯⋯−a1n−a2n⋮d−ann
(1),将第2~n行分别加到第一行,可得第一行的元素为:
[
d
1
+
∑
i
=
1
n
(
−
a
i
1
)
,
d
2
+
∑
i
=
1
n
(
−
a
i
2
)
,
.
.
.
,
d
n
+
∑
i
=
1
n
(
−
a
i
n
)
]
(2)
\tag{2} [d_1+\sum_{i=1}^{n}(-a_{i1}),\,d_2+\sum_{i=1}^{n}(-a_{i2}), ...,\,d_n+\sum_{i=1}^{n}(-a_{in})]
[d1+i=1∑n(−ai1),d2+i=1∑n(−ai2),...,dn+i=1∑n(−ain)](2),因为度矩阵对角线元素是邻接矩阵对应行(列)的和,因此有:
d
1
=
∑
i
=
1
n
(
a
i
1
)
,
d
2
=
∑
i
=
1
n
(
a
i
2
)
,
.
.
.
,
d
n
=
∑
i
=
1
n
(
a
i
n
)
d_1=\sum_{i=1}^{n}(a_{i1}),\,\,\,d_2=\sum_{i=1}^{n}(a_{i2}),\,\,\,...,d_n=\sum_{i=1}^{n}(a_{in})
d1=i=1∑n(ai1),d2=i=1∑n(ai2),...,dn=i=1∑n(ain),所以
(
2
)
(2)
(2) 的元素全为0,即
∣
L
∣
=
0
|L|=0
∣L∣=0。
1.1.2 标准化拉普拉斯是非满秩矩阵
其次,证明标准化拉普拉斯矩阵 L n o r m L^{norm} Lnorm 是非满秩矩阵:
∵
∣
L
n
o
r
m
∣
=
∣
D
−
1
2
L
D
−
1
2
∣
=
∣
D
−
1
2
∣
∣
L
∣
∣
D
−
1
2
∣
\because |L^{norm}|=|D^{-\frac 1 2}LD^{-\frac 1 2}|=|D^{-\frac 1 2}||L||D^{-\frac 1 2}|
∵∣Lnorm∣=∣D−21LD−21∣=∣D−21∣∣L∣∣D−21∣,
∣
L
∣
=
0
|L|=0
∣L∣=0
∴
∣
L
n
o
r
m
∣
=
0
\therefore |L^{norm}|=0
∴∣Lnorm∣=0
1.1.3 拉普拉斯矩阵及标准化拉普拉斯矩阵特征值与特征向量之间的关系
上一节我们知道,拉普拉斯矩阵 L L L 和标准化拉普拉斯矩阵 L n o r m L^{norm} Lnorm 都是非满秩矩阵,都有至少一个特征值为 0。设 e e e 是 L L L 的一个对应于特征值 0 的特征向量,有 L e = 0 Le=0 Le=0。因为:
L n o r m D 1 2 e = D − 1 2 L D − 1 2 D 1 2 e = D − 1 2 ( L e ) = 0 L^{norm} D^{\frac 1 2}e=D^{-\frac 1 2}LD^{-\frac 1 2}D^{\frac 1 2}e=D^{-\frac 1 2}(Le)=0 LnormD21e=D−21LD−21D21e=D−21(Le)=0
所以 D 1 2 e D^{\frac 1 2}e D21e 是 L n o r m L^{norm} Lnorm 的一个对应于特征值 0 的特征向量。
1.2 标准化拉普拉斯矩阵是半正定矩阵
1.2.1 标准化邻接矩阵的二次型化简
设 A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ] , D = [ d 1 d 2 ⋱ d n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix},\,D =\begin{bmatrix} d_1 & & & \\ & d_2 & & \\ & & \ddots & \\ & & & d_n \\ \end{bmatrix} A= a11a21⋮an1a12a22⋮an2⋯⋯⋯a1na2n⋮ann ,D= d1d2⋱dn ,则 D − 1 2 = [ 1 d 1 1 d 2 ⋱ 1 d n ] D^{-\frac 1 2} =\begin{bmatrix} {\frac 1 {\sqrt{d_1}}} & & & \\ & {\frac 1 {\sqrt{d_2}}} & & \\ & & \ddots & \\ & & & {\frac 1 {\sqrt{d_n}}} \\ \end{bmatrix} D−21= d11d21⋱dn1
标准化邻接矩阵
A
n
o
r
m
=
D
−
1
2
A
D
−
1
2
=
[
a
11
d
1
d
1
a
12
d
2
d
1
⋯
a
1
n
d
2
d
n
a
21
d
2
d
1
a
22
d
2
d
2
⋯
a
2
n
d
2
d
n
⋮
⋮
⋮
a
n
1
d
n
d
1
a
n
1
d
n
d
1
⋯
a
n
n
d
n
d
n
]
\text{标准化邻接矩阵} \,\,A^{norm} = D^{-\frac 1 2}AD^{-\frac 1 2}= \begin{bmatrix} {\frac {a_{11}} {\sqrt{d_1d_1}}} & {\frac {a_{12}} {\sqrt{d_2d_1}}} & \cdots & {\frac {a_{1n}} {\sqrt{d_2d_n}}} \\ {\frac {a_{21}} {\sqrt{d_2d_1}}} & {\frac {a_{22}} {\sqrt{d_2d_2}}} & \cdots & {\frac {a_{2n}} {\sqrt{d_2d_n}}} \\ \vdots & \vdots & & \vdots \\ {\frac {a_{n1}} {\sqrt{d_nd_1}}} & {\frac {a_{n1}} {\sqrt{d_nd_1}}} & \cdots & {\frac {a_{nn}} {\sqrt{d_nd_n}}} \\ \end{bmatrix}
标准化邻接矩阵Anorm=D−21AD−21=
d1d1a11d2d1a21⋮dnd1an1d2d1a12d2d2a22⋮dnd1an1⋯⋯⋯d2dna1nd2dna2n⋮dndnann
,令
x
=
[
x
1
,
x
2
,
⋯
,
x
n
]
T
\bold{x}=[x_1, x_2,\cdots, x_n]^T
x=[x1,x2,⋯,xn]T,则:
x
T
A
n
o
r
m
x
=
[
x
1
,
x
2
,
⋯
,
x
n
]
[
a
11
d
1
d
1
a
12
d
2
d
1
⋯
a
1
n
d
2
d
n
a
21
d
2
d
1
a
22
d
2
d
2
⋯
a
2
n
d
2
d
n
⋮
⋮
⋮
a
n
1
d
n
d
1
a
n
1
d
n
d
1
⋯
a
n
n
d
n
d
n
]
[
x
1
x
2
⋮
x
n
]
=
[
∑
i
n
x
i
a
i
1
d
i
d
1
,
∑
i
n
x
i
a
i
2
d
i
d
2
,
⋯
,
∑
i
n
x
i
a
i
n
d
i
d
n
]
[
x
1
x
2
⋮
x
n
]
=
∑
i
n
x
i
x
1
a
i
1
d
i
d
1
+
∑
i
n
x
i
x
2
a
i
2
d
i
d
2
+
⋯
+
∑
i
n
x
i
x
n
a
i
n
d
i
d
n
=
∑
i
,
j
n
x
i
x
j
a
i
j
d
i
d
j
=
∑
(
i
,
j
)
∈
E
2
x
i
x
j
a
i
j
d
i
d
j
(
因为
a
i
j
=
a
j
i
,
所以有个
2
;
a
i
j
∈
{
0
,
1
}
,
所以可以消去
.
)
\begin{aligned} \bold{x}^TA^{norm}\bold{x}&=[x_1, x_2,\cdots, x_n] \begin{bmatrix} {\frac {a_{11}} {\sqrt{d_1d_1}}} & {\frac {a_{12}} {\sqrt{d_2d_1}}} & \cdots & {\frac {a_{1n}} {\sqrt{d_2d_n}}} \\ {\frac {a_{21}} {\sqrt{d_2d_1}}} & {\frac {a_{22}} {\sqrt{d_2d_2}}} & \cdots & {\frac {a_{2n}} {\sqrt{d_2d_n}}} \\ \vdots & \vdots & & \vdots \\ {\frac {a_{n1}} {\sqrt{d_nd_1}}} & {\frac {a_{n1}} {\sqrt{d_nd_1}}} & \cdots & {\frac {a_{nn}} {\sqrt{d_nd_n}}} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{bmatrix} \\ &=\begin{bmatrix} \sum_i^n{\frac {x_ia_{i1}} {\sqrt{d_id_1}}},\, \sum_i^n{\frac {x_ia_{i2}} {\sqrt{d_id_2}}},\, \cdots,\, \sum_i^n{\frac {x_ia_{in}} {\sqrt{d_id_n}}} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{bmatrix} \\ &= \sum_i^n{\frac {x_ix_1a_{i1}} {\sqrt{d_id_1}}}+ \sum_i^n{\frac {x_ix_2a_{i2}} {\sqrt{d_id_2}}}+ \cdots+ \sum_i^n{\frac {x_ix_na_{in}} {\sqrt{d_id_n}}} \\ &=\sum_{i,j}^n{\frac {x_ix_ja_{ij}} {\sqrt{d_id_j}}} \\ &=\sum_{(i,j)\in E}{\frac {2x_ix_ja_{ij}} {\sqrt{d_id_j}}} \,\,\,\,(因为a_{ij}=a_{ji},所以有个2;a_{ij}\in\{0,1\},所以可以消去.) \end{aligned}
xTAnormx=[x1,x2,⋯,xn]
d1d1a11d2d1a21⋮dnd1an1d2d1a12d2d2a22⋮dnd1an1⋯⋯⋯d2dna1nd2dna2n⋮dndnann
x1x2⋮xn
=[∑indid1xiai1,∑indid2xiai2,⋯,∑indidnxiain]
x1x2⋮xn
=i∑ndid1xix1ai1+i∑ndid2xix2ai2+⋯+i∑ndidnxixnain=i,j∑ndidjxixjaij=(i,j)∈E∑didj2xixjaij(因为aij=aji,所以有个2;aij∈{0,1},所以可以消去.),其中
E
E
E 为边的集合。
1.2.2 标准化拉普拉斯矩阵是半正定矩阵的证明
对
∀
x
∈
R
n
\forall \bold{x}\in \mathbb{R}^n
∀x∈Rn,
L
n
o
r
m
L^{norm}
Lnorm的二次型为:
x
T
L
n
o
r
m
x
=
x
T
(
I
−
A
n
o
r
m
)
x
=
∑
i
∈
V
x
i
2
−
∑
(
i
,
j
)
∈
E
2
x
i
x
j
d
i
d
j
=
∑
(
i
,
j
)
∈
E
(
x
i
2
d
i
+
x
j
2
d
j
)
−
∑
(
i
,
j
)
∈
E
2
x
i
x
j
d
i
d
j
=
∑
(
i
,
j
)
∈
E
(
x
i
d
i
−
x
j
d
j
)
2
≥
0
\begin{aligned} \bold{x}^TL^{norm}\bold{x}&=\bold{x}^T\Big(I-A^{norm}\Big)\bold{x} \\ &=\sum_{i\in V}x_i^2-\sum_{(i,j)\in E}{\frac {2x_ix_j} {\sqrt{d_id_j}}} \\ &=\sum_{(i,j)\in E}\Bigg({\frac {x_i^2} {d_i}}+{\frac {x_j^2} {d_j}}\Bigg)-\sum_{(i,j)\in E}{\frac {2x_ix_j} {\sqrt{d_id_j}}} \\ &=\sum_{(i,j)\in E}\Bigg({\frac {x_i} {\sqrt{d_i}}}-{\frac {x_j} {\sqrt{d_j}}}\Bigg)^2\\ &\ge0 \end{aligned}
xTLnormx=xT(I−Anorm)x=i∈V∑xi2−(i,j)∈E∑didj2xixj=(i,j)∈E∑(dixi2+djxj2)−(i,j)∈E∑didj2xixj=(i,j)∈E∑(dixi−djxj)2≥0,根据半正定矩阵的定义可知,
L
n
o
r
m
L^{norm}
Lnorm 为半正定矩阵。
1.3 标准化邻接矩阵的特征值范围
1.3.1 瑞利商(Rayleigh quotient)
在求标准化邻接矩阵
A
n
o
r
m
A^{norm}
Anorm 的特征值范围前,需要了解瑞利商。瑞利商的定义如下:
R
(
A
,
x
)
=
x
T
A
x
x
T
x
R(A,x)=\frac{x^TAx}{x^Tx}
R(A,x)=xTxxTAx,其中
A
A
A 为
n
×
n
n\times n
n×n 对称矩阵,
x
x
x 为
n
n
n 维度向量。如果A的特征值为
λ
1
≤
λ
2
≤
⋯
≤
λ
n
\lambda_1\le\lambda_2\le\cdots\le\lambda_n
λ1≤λ2≤⋯≤λn,则其瑞利商的下界为
λ
1
\lambda_{1}
λ1,上界为
λ
n
\lambda_{n}
λn。
关于瑞利商,参见我的博客:瑞利商性质及证明。
1.3.2 标准化邻接矩阵的特征值范围计算
x T L n o r m x ≥ 0 ⇒ x T ( I − A n o r m ) x ≥ 0 ⇒ x T x − x T A n o r m x ≥ 0 ⇒ 1 ≥ x T A n o r m x x T x x^TL^{norm}x\ge0\rArr x^T(I-A^{norm})x\ge0\rArr x^Tx-x^TA^{norm}x\ge0\rArr 1\ge{\frac {x^TA^{norm}x} {x^Tx}} xTLnormx≥0⇒xT(I−Anorm)x≥0⇒xTx−xTAnormx≥0⇒1≥xTxxTAnormx,由瑞利商的性质可知, A n o r m A^{norm} Anorm 最大特征值小于等于1,即 α n ≤ 1 \alpha_n\le1 αn≤1;当 x = D 1 2 e x=D^{\frac 1 2}e x=D21e 时, α n = 1 \alpha_n=1 αn=1。
类似于证明 L n o r m L^{norm} Lnorm 是半正定矩阵, I + A n o r m I+A^{norm} I+Anorm 也是半正定矩阵:
x
T
(
I
+
A
n
o
r
m
)
x
=
∑
i
∈
V
x
i
2
+
∑
(
i
,
j
)
∈
E
(
x
i
d
i
+
x
j
d
j
)
2
≥
0
x^T(I+A^{norm})x=\sum_{i\in V}x_i^2+\sum_{(i,j)\in E}\Big( {\frac {x_i} {\sqrt{d_i}}}+{\frac {x_j} {\sqrt{d_j}}} \Big)^2\ge0
xT(I+Anorm)x=i∈V∑xi2+(i,j)∈E∑(dixi+djxj)2≥0,所以有:
x
T
(
I
+
A
n
o
r
m
)
x
≥
0
⇒
x
T
x
+
x
T
A
n
o
r
m
x
≥
0
⇒
x
T
A
n
o
r
m
x
x
T
x
≥
−
1
x^T(I+A^{norm})x\ge0\rArr x^Tx+x^TA^{norm}x\ge0\rArr {\frac {x^TA^{norm}x} {x^Tx}}\ge-1
xT(I+Anorm)x≥0⇒xTx+xTAnormx≥0⇒xTxxTAnormx≥−1,由瑞利商的性质可知,
A
n
o
r
m
A^{norm}
Anorm 最小特征值大于等于-1,即
α
1
≥
−
1
\alpha_1\ge-1
α1≥−1。
所以标准化邻接矩阵 A n o r m A^{norm} Anorm 的特征值满足 − 1 ≤ α 1 ≤ α 2 ≤ ⋯ ≤ α n = 1 -1\le\alpha_1\le\alpha_2\le\cdots\le\alpha_n=1 −1≤α1≤α2≤⋯≤αn=1
1.3.3 标准化拉普拉斯矩阵的特征值范围计算
∵
\because
∵
x
T
L
n
o
r
m
x
x
T
x
=
x
T
(
I
−
A
n
o
r
m
)
x
x
T
x
=
1
−
x
T
A
n
o
r
m
x
x
T
x
=
1
−
R
(
A
n
o
r
m
,
x
)
−
1
≤
R
(
A
n
o
r
m
,
x
)
≤
1
\begin{aligned} &\frac {x^TL^{norm}x} {x^Tx}=\frac {x^T(I-A^{norm})x} {x^Tx}=1-\frac {x^TA^{norm}x} {x^Tx}=1-R(A^{norm},x) \\ &-1\le R(A^{norm},x)\le1 \end{aligned}
xTxxTLnormx=xTxxT(I−Anorm)x=1−xTxxTAnormx=1−R(Anorm,x)−1≤R(Anorm,x)≤1
∴
\therefore
∴
0
≤
x
T
L
n
o
r
m
x
x
T
x
≤
2
\begin{aligned} &0\le \frac {x^TL^{norm}x} {x^Tx} \le2 \end{aligned}
0≤xTxxTLnormx≤2,其下确界为0,当
x
=
D
1
2
e
x=D^{\frac 1 2}e
x=D21e 时,
λ
1
=
0
\lambda_1=0
λ1=0。
证毕。
参考网址
拉普拉斯性质
ORIE 6334 Spectral Graph Theory Lecture 7(主要参考了本文)
瑞利商性质及证明
Bounding matrix quadratic form using eigenvalues
Why Laplacian Matrix need normalization and how come the sqrt of Degree Matrix?文章来源:https://www.toymoban.com/news/detail-669082.html
■ \blacksquare ■文章来源地址https://www.toymoban.com/news/detail-669082.html
到了这里,关于标准化拉普拉斯矩阵特征值范围为什么小于等于2?(证明)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!