高等数学：线性代数-第一章

第1章 行列式

1.1 全排列和对换

全排列 把 n 个不同的元素排成一列，叫做这 n 个元素的全排列，简称排列。

例如, { 5 , 3 , 4 , 2 , 1 } \{ 5, 3, 4, 2, 1 \} {5,3,4,2,1} 是一个排列。

全排列的个数 记 $P_n$ 为 n 个元素的全排列的个数，则有
$$P_n=n!$$
排列数 记 $P_n^m$ 为从 n 个不同的元素中取出 m 个元素的全排列的个数，则有
$$P_n^m=A_n^m=\frac{n!}{(n-m)!}$$
特别地，当 m=n 时， $P_n^m=P_n$成立。

逆序 在全排列中，当某一对元素的先后次序与标准次序不同时，就说它构成 1 个逆序。

逆序数 一个排列中所有逆序的总数叫做这个排列的逆序数。记排列 $a_n$ 的逆序数为 t ，则有
$$t=\sum _{i=1}^n\sum _{j=1}^{i-1}[a_i<a_j]$$
奇排列与偶排列 逆序数为奇数的排列叫做奇排列，逆序数为偶数的排列叫做偶排列。

对换 在排列中，将任意两个元素对调，其余的元素不动的操作叫做对换。特别地，将相邻的两个元素对换，叫做相邻对换。

对换定理 一个排列中的任意两个元素对换，排列改变奇偶性。

1.2 n阶行列式

$\mathbf{n}$ 阶行列式 设有 $n^2$个数，排成 n 行 n 列的数表
$$\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}$$
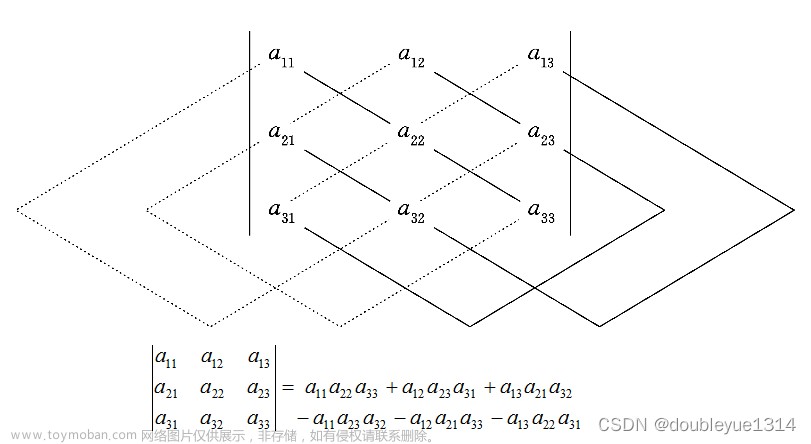
定义 n! 项代数和
$$
D = \sum_{i = 1}^{n} (-1)^{t}\prod_{j = 1}^{n} a_{jp_{j}} \
$
其中 $p_1,p_2,\cdots ,p_n$为 n 的所有排列， t 为排列 $p_n$ 的逆序数。则称上式为n 阶行列式，记作

D = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ D = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} \\ D= ​a11​a21​⋮an1​​a12​a22​⋮an2​​⋯⋯⋱⋯​a1n​a2n​⋮ann​​ ​
简记作 $\det (a_{ij})$，其中 $a_{ij}$ 为行列式 D 的 (i,j) 元。

上（下）三角行列式 主对角线以下（上）的元素都为 0 的行列式叫做上（下）三角行列式；特别地，除主对角线以外，其余元素都为 0 的行列式叫做对角行列式。

上（下）三角行列式和对角行列式满足
∣ a 11 a 21 a 22 ⋮ ⋮ ⋱ a n 1 a n 2 ⋯ a n n ∣ = ∏ i = 1 n a i i ∣ λ 1 λ 2 ⋱ λ n ∣ = ∏ i = 1 n λ i \begin{vmatrix} a_{11} & & & \\ a_{21} & a_{22} & & \\ \vdots & \vdots & \ddots & \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} = \prod_{i = 1}^{n}{a_{ii}} \\ \begin{vmatrix} \lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n} \\ \end{vmatrix} = \prod_{i = 1}^{n}{\lambda_{i}} \\ ​a11​a21​⋮an1​​a22​⋮an2​​⋱⋯​ann​​ ​=i=1∏n​aii​ ​λ1​​λ2​​⋱​λn​​ ​=i=1∏n​λi​

1.3 行列式的性质

性质1 行列式 D 与它的转置行列式 D^{T} 相等，即
$$\det (a_{ij})=\det (a_{ji})$$
性质2 对换行列式的两行（列），行列式变号。

性质2推论 若行列式 D 存在两行（列）完全相同，则 D = 0 .

性质3 行列式的某一行（列）中的所有元素都乘同一数 k ，等于用数 k 乘此行列式，即
$$\begin{gathered} D\stackrel{r_i\times k}{}kD \\ D\stackrel{c_j\times k}{}kD \end{gathered}$$
性质4 若行列式 D 中存在两行（列）元素成比例，则 D = 0 .

性质5 若行列式 D 的某一行（列）的元素都是两数之和，则行列式 D 满足
D = ∣ a 11 a 12 ⋯ a 1 n ⋮ ⋮ ⋮ a i 1 + a i 1 ′ a i 2 + a i 2 ′ ⋯ a i n + a i n ′ ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∣ a 11 a 12 ⋯ a 1 n ⋮ ⋮ ⋮ a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ∣ + ∣ a 11 a 12 ⋯ a 1 n ⋮ ⋮ ⋮ a i 1 ′ a i 2 ′ ⋯ a i n ′ ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ∣ \begin{align} D &= \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1} + a_{i1}^{\prime} & a_{i2} + a_{i2}^{\prime} & \cdots & a_{in} + a_{in}^{\prime} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} \\ &= \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} + \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1}^{\prime} & a_{i2}^{\prime} & \cdots & a_{in}^{\prime} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} \\ \end{align} \\ D​= ​a11​⋮ai1​+ai1′​⋮an1​​a12​⋮ai2​+ai2′​⋮an2​​⋯⋯⋯​a1n​⋮ain​+ain′​⋮ann​​ ​= ​a11​⋮a21​⋮an1​​a12​⋮a22​⋮an2​​⋯⋯⋯​a1n​⋮a2n​⋮ann​​ ​+ ​a11​⋮ai1′​⋮an1​​a12​⋮ai2′​⋮an2​​⋯⋯⋯​a1n​⋮ain′​⋮ann​​ ​​​
性质6 把行列式 D 的某一行（列）的各元素的 k 倍加到另一行（列），行列式不变，即
$$\begin{gathered} D\stackrel{r_j+k{r}_i}{}kD \\ D\stackrel{c_q+k{c}_p}{}kD \end{gathered}$$
分块（矩阵）行列式 设
D = ∣ a 11 ⋯ a 1 k ⋮ ⋮ a k 1 ⋯ a k k c 11 ⋯ c 1 k b 11 ⋯ b 1 n ⋮ ⋮ ⋮ ⋮ c n 1 ⋯ c n k b n 1 ⋯ b n n ∣ = ∣ A O C B ∣ D = \begin{vmatrix} a_{11} & \cdots & a_{1k} & & & & \\ \vdots & & \vdots & & & & \\ a_{k1} & \cdots & a_{kk} & & & & \\ c_{11} & \cdots & c_{1k} & b_{11} & \cdots & b_{1n} & \\ \vdots & & \vdots & \vdots & & \vdots & \\ c_{n1} & \cdots & c_{nk} & b_{n1} & \cdots & b_{nn} & \\ \end{vmatrix} = \begin{vmatrix} A & O \\ C & B \\ \end{vmatrix} \\ D= ​a11​⋮ak1​c11​⋮cn1​​⋯⋯⋯⋯​a1k​⋮akk​c1k​⋮cnk​​b11​⋮bn1​​⋯⋯​b1n​⋮bnn​​​ ​= ​AC​OB​ ​
则有
D = ∣ a 11 ⋯ a 1 k ⋮ ⋮ a k 1 ⋯ a k k ∣ ∣ b 11 ⋯ b 1 n ⋮ ⋮ b n 1 ⋯ b n n ∣ = A B D = \begin{vmatrix} a_{11} & \cdots & a_{1k} \\ \vdots & & \vdots \\ a_{k1} & \cdots & a_{kk} \\ \end{vmatrix} \begin{vmatrix} b_{11} & \cdots & b_{1n} \\ \vdots & & \vdots \\ b_{n1} & \cdots & b_{nn} \\ \end{vmatrix} = AB \\ D= ​a11​⋮ak1​​⋯⋯​a1k​⋮akk​​ ​ ​b11​⋮bn1​​⋯⋯​b1n​⋮bnn​​ ​=AB
类似地，有
∣ A C O B ∣ = A B \begin{vmatrix} A & C \\ O & B \\ \end{vmatrix} =AB \\ ​AO​CB​ ​=AB

1.4 行列式按行（列）展开

余子式 在 n 阶行列式中，把 $a_{ij}$ 所在的行和列划去后，留下的 n-1 阶行列式叫做 $a_{ij}$的余子式，记作 $M_{ij}$ .

代数余子式 记
$$A_{ij}=(-1{)}^{i+j}{M}_{ij}$$
则 $A_{ij}$ 叫做 $a_{ij}$的代数余子式。

行列式按行（列）展开法则 行列式 D 等于它任一行（列）的各元素与其对应的代数余子式乘积之和，即
$$D=\sum _{i=1}^n{a}_{pi}{A}_{pi}=\sum _{i=1}^n{a}_{iq}{A}_{iq}$$
Vandermonde行列式
D n = ∣ 1 1 ⋯ 1 x 1 x 2 ⋯ x n x 1 2 x 2 2 ⋯ x n 2 ⋮ ⋮ ⋱ ⋮ x 1 n − 1 x 2 n − 1 ⋯ x n n − 1 ∣ = ∏ n ≥ i > j ≥ 1 ( x i − x j ) D_{n} = \begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_{1} & x_{2} & \cdots & x_{n} \\ x_{1}^{2} & x_{2}^{2} & \cdots & x_{n}^{2} \\ \vdots & \vdots & \ddots & \vdots \\ x_{1}^{n - 1} & x_{2}^{n - 1} & \cdots & x_{n}^{n - 1} \\ \end{vmatrix} = \prod_{n \geq i > j \geq 1}(x_{i} - x_{j}) \\ Dn​= ​1x1​x12​⋮x1n−1​​1x2​x22​⋮x2n−1​​⋯⋯⋯⋱⋯​1xn​xn2​⋮xnn−1​​ ​=n≥i>j≥1∏​(xi​−xj​)文章来源地址https://www.toymoban.com/news/detail-669152.html

到了这里，关于高等数学：线性代数-第一章的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！