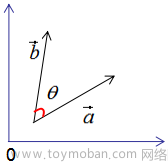
线性代数是一门将 m 维世界与 n 维世界联系起来的学科
1 集合相关知识
1.1 映射与像
映射:把集合 Y 的元素与集合 X 的元素相对应的规则叫做 “从集合 X 到集合 Y 的映射”。
像:通过映射 f 与 xi 相对应的集合 Y 的元素,叫做 xi通过映射 f 形成的像,一般表示为 f(xi)。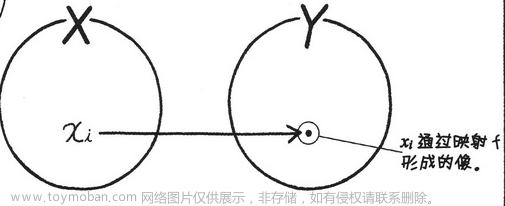
1.2 映射与像
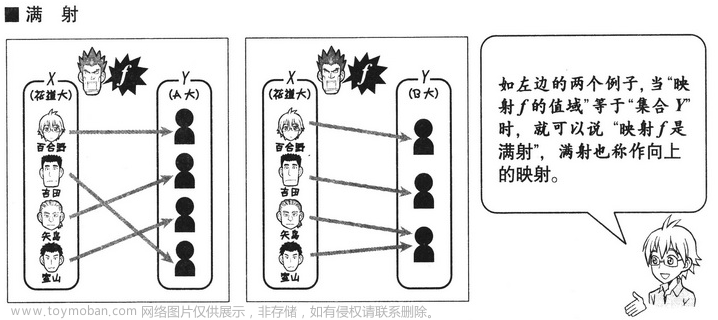
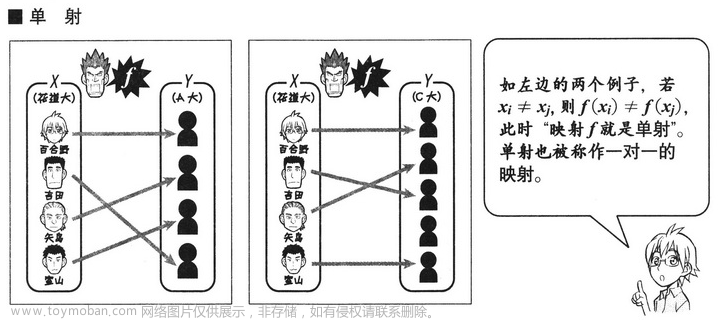
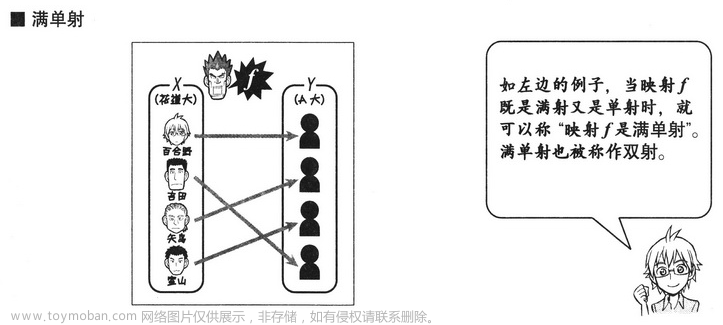

1.3 线性映射

线性映射的例子
f
(
x
)
=
2
x
f(x) = 2x
f(x)=2x
两个条件均满足,条件证明:
不是线性映射的例子
f
(
x
)
=
2
x
−
1
f(x)=2x-1
f(x)=2x−1
满足条件 1,但是不满足条件 2:
2 矩阵
一次方程使用矩阵表示:
2.1 特殊矩阵
2.1.1 零矩阵

2.1.2 转置矩阵
2.1.3 对称矩阵
以对角元素为中心线对称的 n 阶方阵
2.1.4 上三角矩阵
对角元素左下角的所有元素均为 0 的 n 阶方阵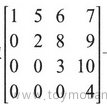
2.1.5 下三角矩阵
对角元素右上角的所有元素均为 0 的 n 阶方阵
2.1.6 对角矩阵
对角元素以外的元素均为 0 的 n 阶方阵,也可以表示为 diag(1,2,3,4)。diag 表示对角线的意思 diagonal。
对角矩阵计算 p 次方: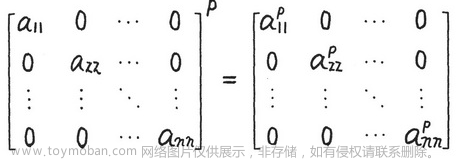
2.1.7 单位矩阵
对角元素均为 1,对角元素以外的其他元素全部为 0 的 n 阶方阵,也即 diag(1,1,…,1)
单位矩阵与任何矩阵相乘,还是得到原矩阵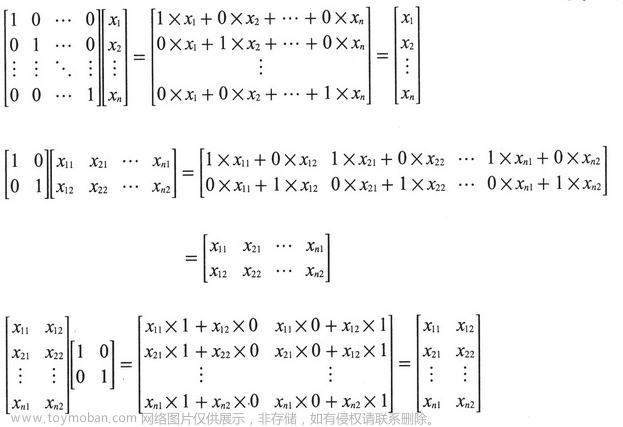
2.1.8 逆矩阵
与 n 阶原方阵 
的积等于单位矩阵的 n 阶方阵就是原方阵的逆矩阵。
原方阵与逆矩阵相乘,不管其顺序如何得到的乘积一定是单位矩阵。
存在逆矩阵的 n 阶方阵叫做可逆矩阵。
2.2 行列式
2.2.1 根据行列式判断是否可逆
计算行列式,det 即为 deterninant(决定因子)。行列式不为 0 则可逆。行列式为 0 ,则不可逆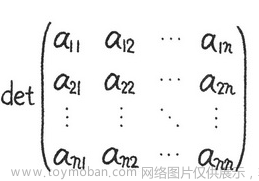
2.2.2 二阶行列式

2.2.3 三阶行列式
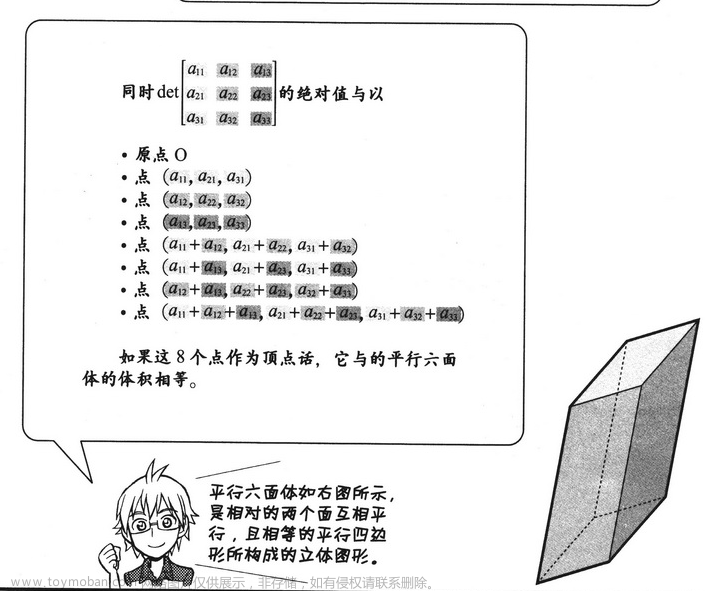
3 向量
3.1 向量的 4 种解释方法
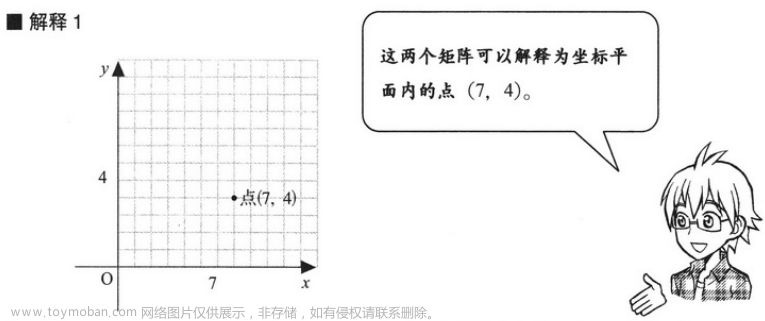
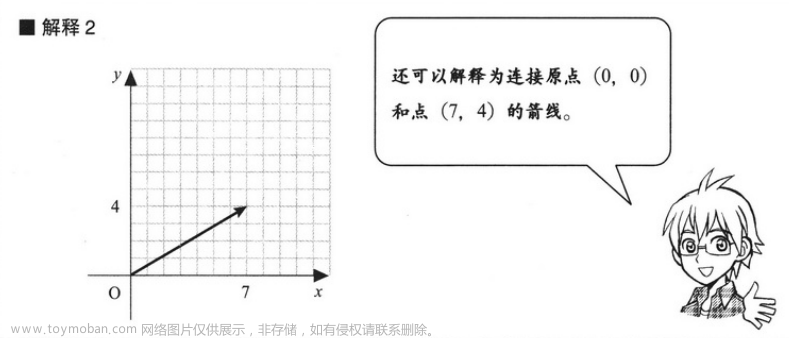
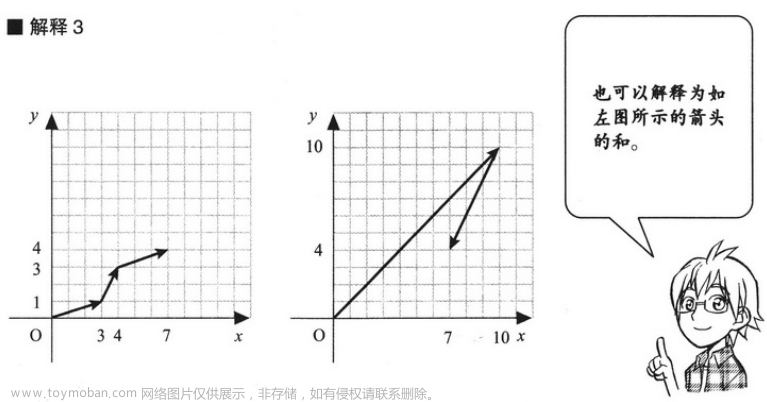
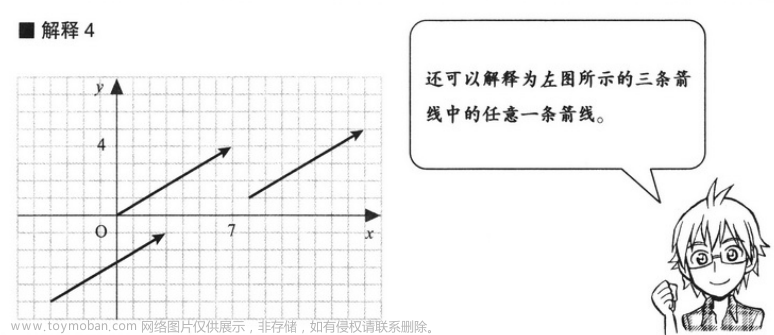
关于解释 4 的说明:虽然这些箭线位置不同,但它们表示的都是从箭尾到箭头的水平长度为 7,垂直长度为 4,所以这些箭线是相等的。
3.2 向量表示直线和空间
把 n × 1 列向量的所有分量的集合表示为 Rn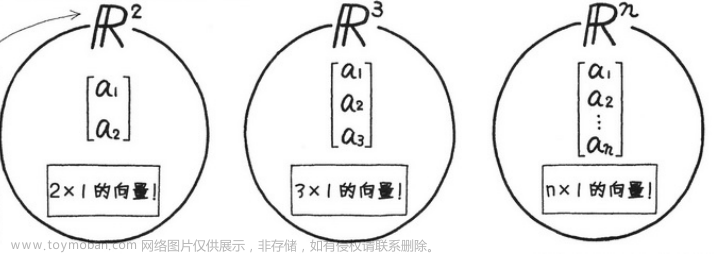
现在利用向量表示点、轴、直线、平面和空间
点,c 为任意实数(关于虚数与复数)。y 轴上的点 (0,c) 可以表示为向量 c
[
0
1
]
∣
\left[ \begin{matrix} 0 \\ 1 \end{matrix}\right]|
[01]∣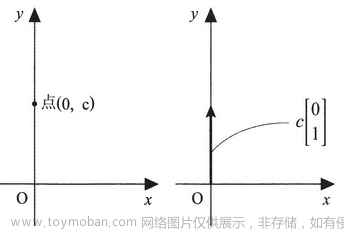
轴,y 轴可以表示为集合
{
c
[
0
1
]
∣
c
为
任
意
实
数
}
\{c\left[ \begin{matrix} 0 \\ 1 \end{matrix} \right]|c为任意实数\}
{c[01]∣c为任意实数}
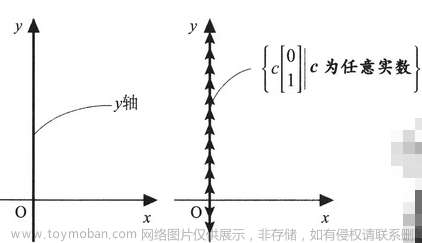
直线,直线 x1=3 可以表示为集合,
{
3
[
1
0
]
+
c
[
0
1
]
∣
c
为
任
意
实
数
}
\{3\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]+c\left[ \begin{matrix} 0 \\ 1 \end{matrix} \right] |c为任意实数\}
{3[10]+c[01]∣c为任意实数}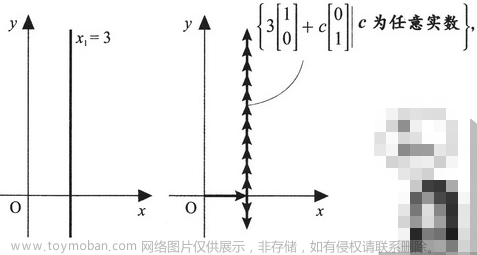
平面1,平面
x
1
x
2
x_1x_2
x1x2 可以表示为集合
{
c
1
[
1
0
]
+
c
2
[
0
1
]
∣
c
1
和
c
2
为
任
意
实
数
}
\{c_1\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]+c_2\left[ \begin{matrix} 0 \\ 1 \end{matrix} \right] |c_1和c_2为任意实数\}
{c1[10]+c2[01]∣c1和c2为任意实数},简而言之就是
R
2
R^2
R2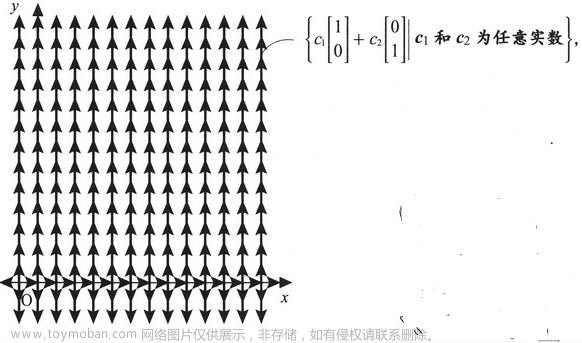
平面2,平面
x
1
x
2
x_1x_2
x1x2 也可以表示为集合
{
c
1
[
3
1
]
+
c
2
[
1
2
]
∣
c
1
和
c
2
为
任
意
实
数
}
\{c_1\left[ \begin{matrix} 3 \\ 1 \end{matrix} \right]+c_2\left[ \begin{matrix} 1 \\ 2 \end{matrix} \right] |c_1和c_2为任意实数\}
{c1[31]+c2[12]∣c1和c2为任意实数},简而言之就是
R
2
R^2
R2
空间1,
x
1
x
2
x
3
x_1x_2x_3
x1x2x3 空间可以表示为集合
{
c
1
[
1
0
0
]
+
c
2
[
0
1
0
]
+
c
3
[
0
0
1
]
∣
c
1
、
c
2
和
c
3
为
任
意
实
数
}
\{c_1\left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right]+c_2\left[ \begin{matrix} 0 \\ 1 \\ 0 \end{matrix} \right]+c_3\left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] |c_1、c_2和 c_3 为任意实数\}
{c1⎣⎡100⎦⎤+c2⎣⎡010⎦⎤+c3⎣⎡001⎦⎤∣c1、c2和c3为任意实数},简而言之就是
R
3
R^3
R3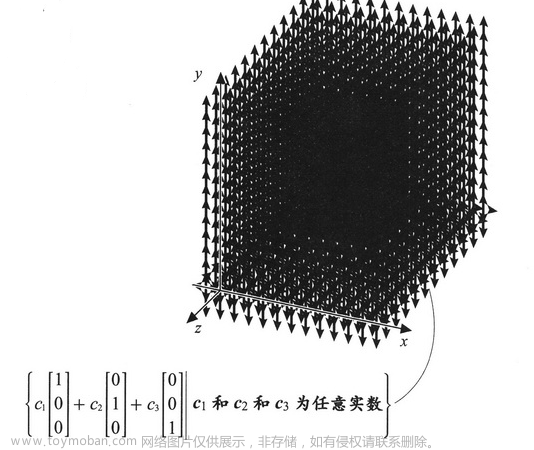
空间2,
x
1
x
2
x
3
.
.
.
x
n
x_1x_2x_3...x_n
x1x2x3...xn 空间可以表示为集合: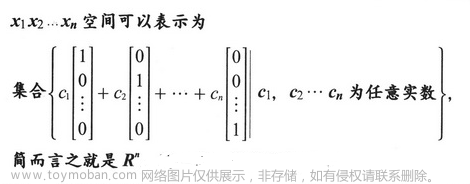
3.3 线性无关
线性无关是限定零向量的概念,也即组成零向量的向量集合只有一组全为 0 的解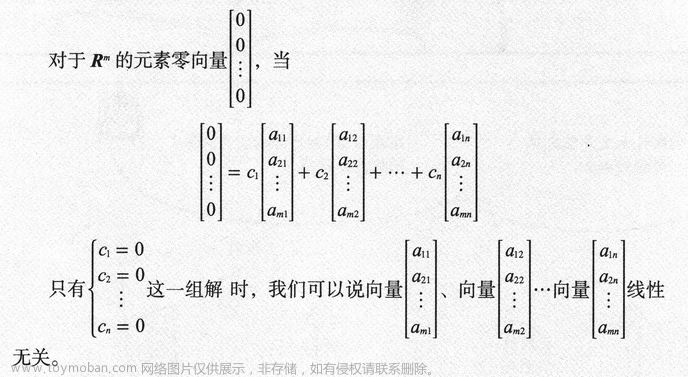
同时,也可以把线性无关叫做线性独立。如果向量之间不是线性无关,就叫做线性相关。
几个线性无关例子: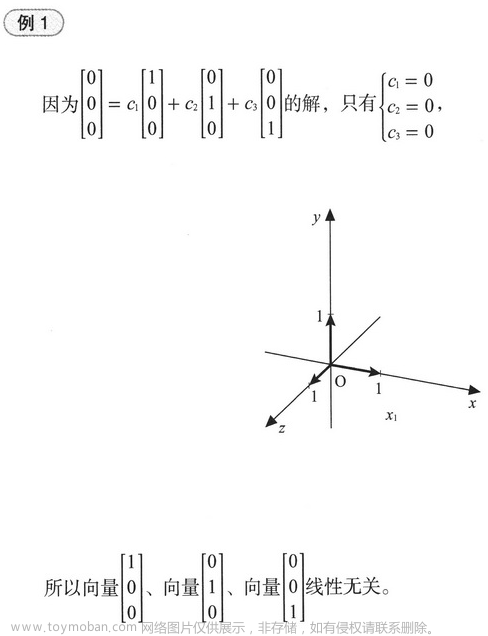
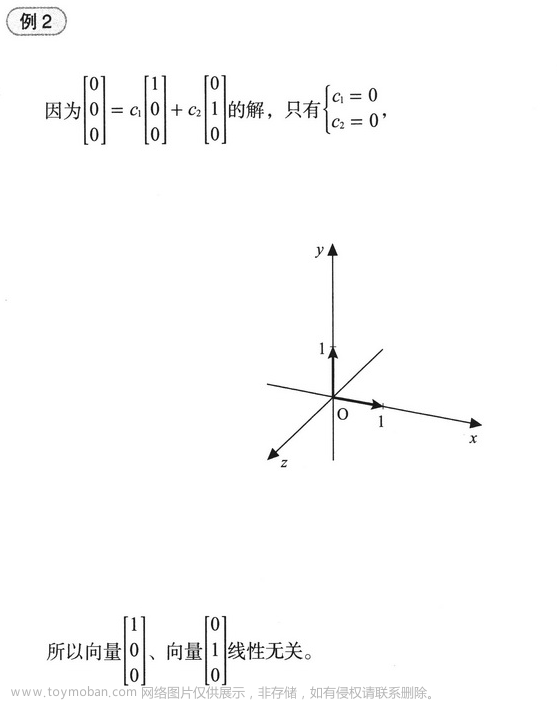
几个线性相关例子: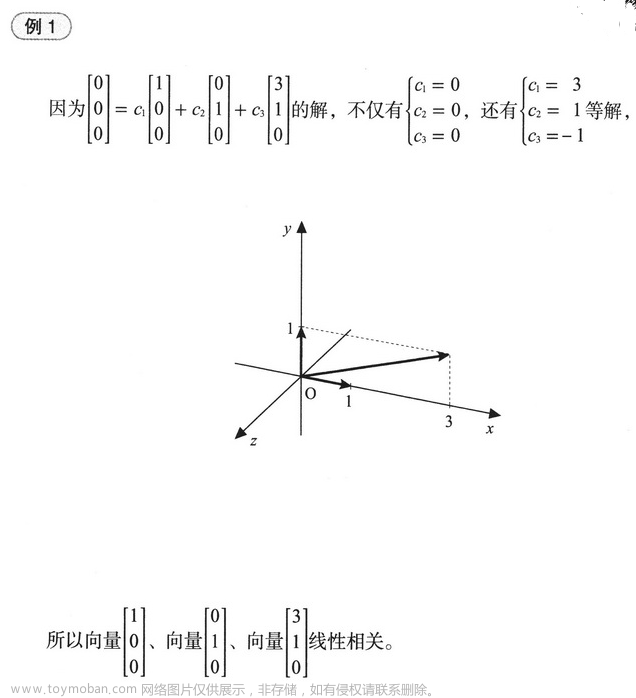
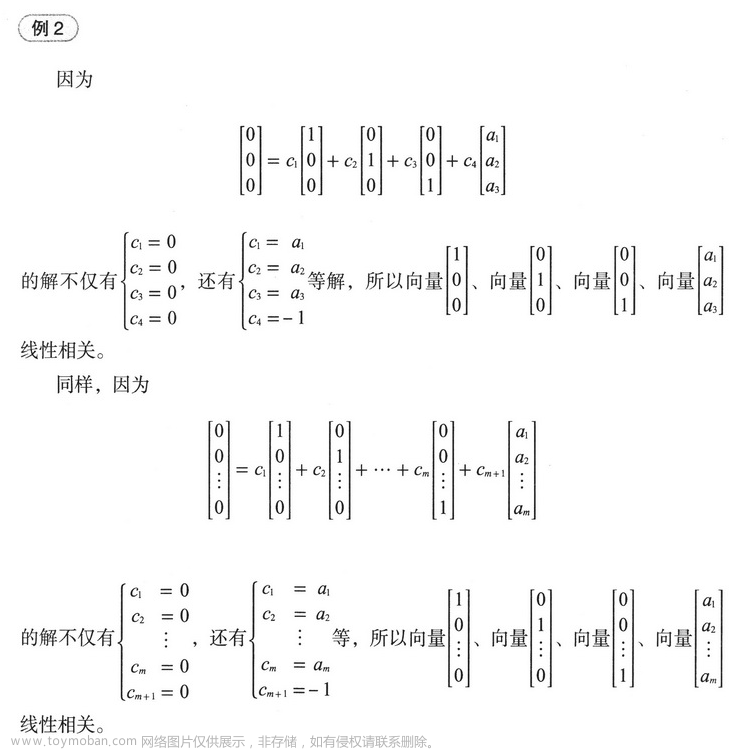
3.4 基
基是一个集合,集合里面的元素是向量。基是以
R
n
R^n
Rn 的所有向量为对象的概念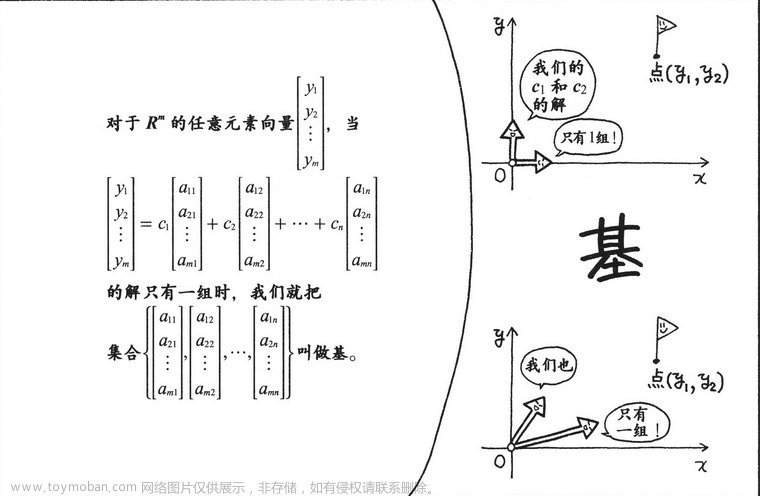
基的例子: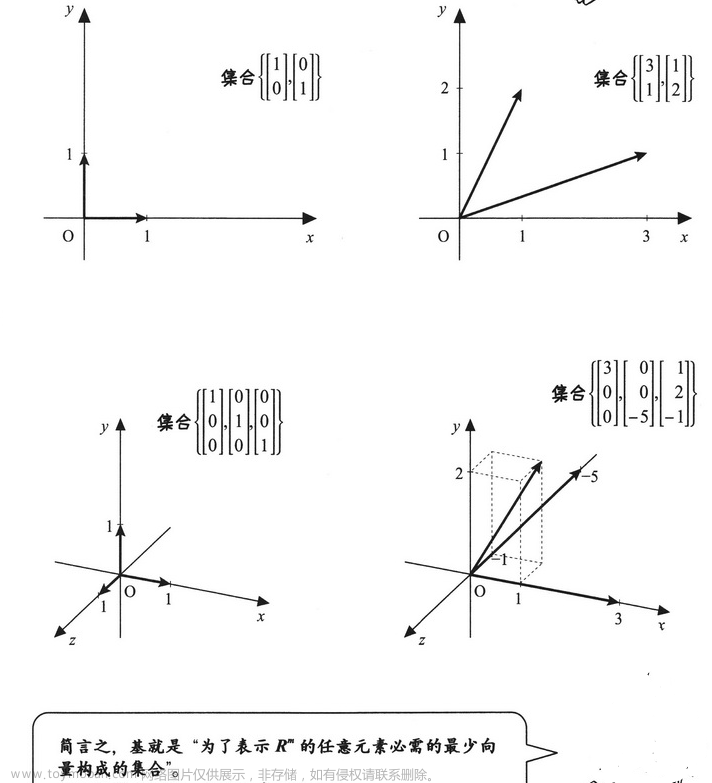
不是基的例子: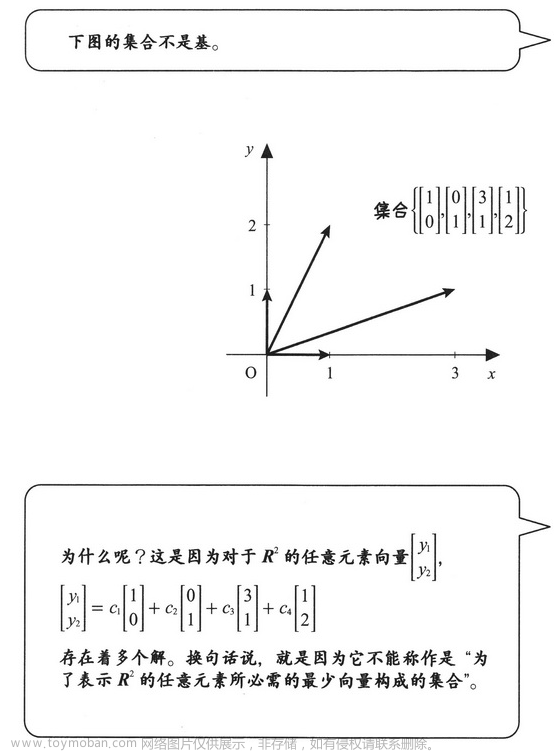
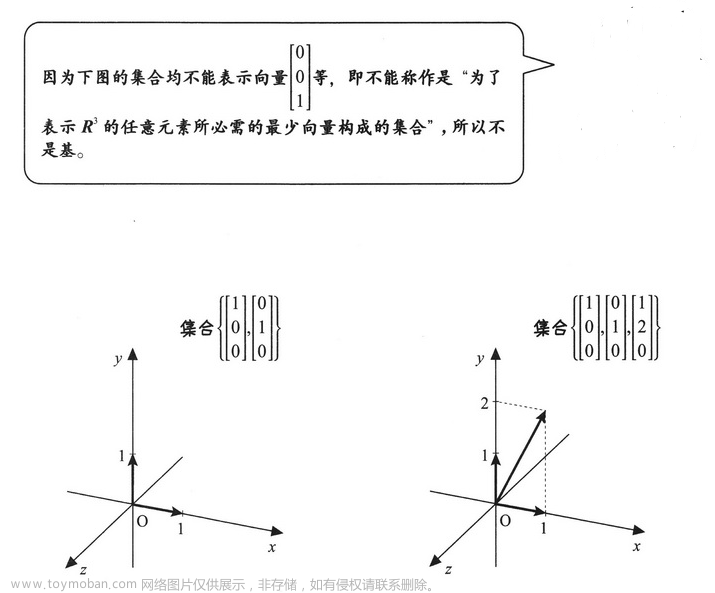
集合
{
[
1
0
0
]
,
[
0
1
0
]
}
\{\left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right],\left[ \begin{matrix} 0 \\ 1 \\ 0 \end{matrix} \right]\}
{⎣⎡100⎦⎤,⎣⎡010⎦⎤},虽然不是基,但是这两个向量线性无关。也就是说线性无关向量集合并不一定是基,反过来也可以说即使集合不是基,起元素也有可能线性无关。
3.5 维数
3.5.1 子空间
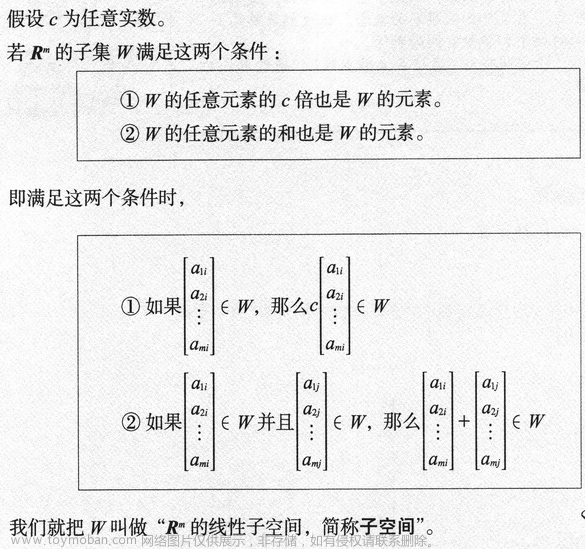
子空间的例子: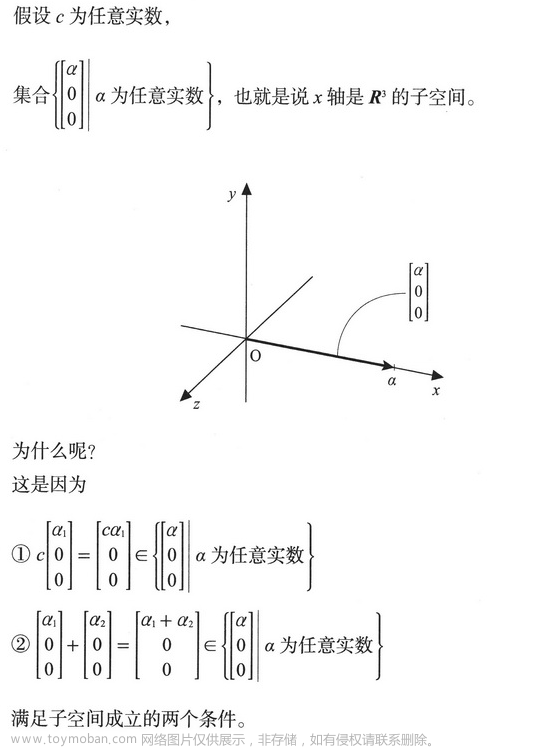
不是子空间的例子: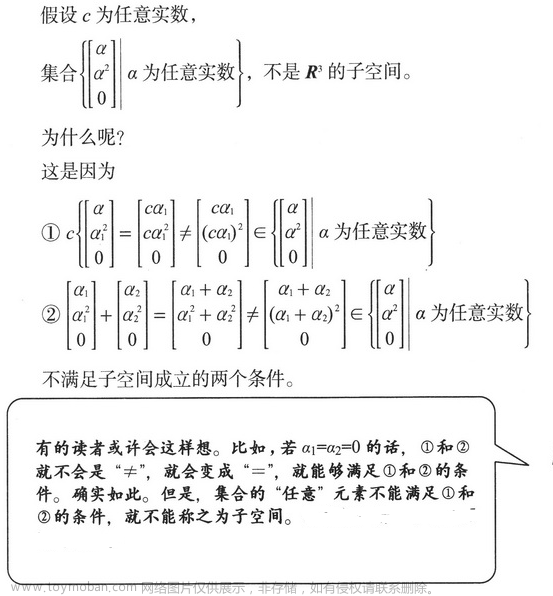
由向量空间生成的子空间: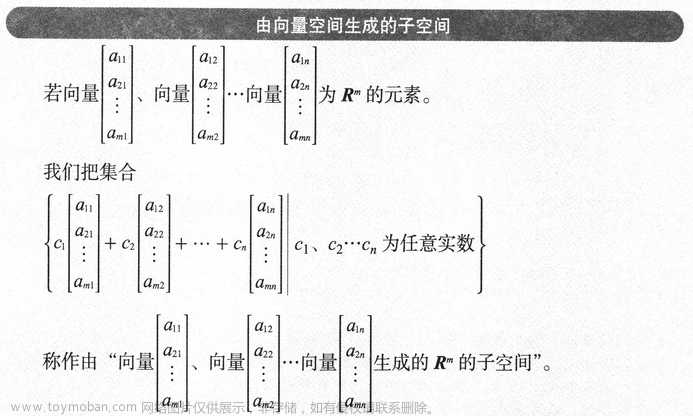
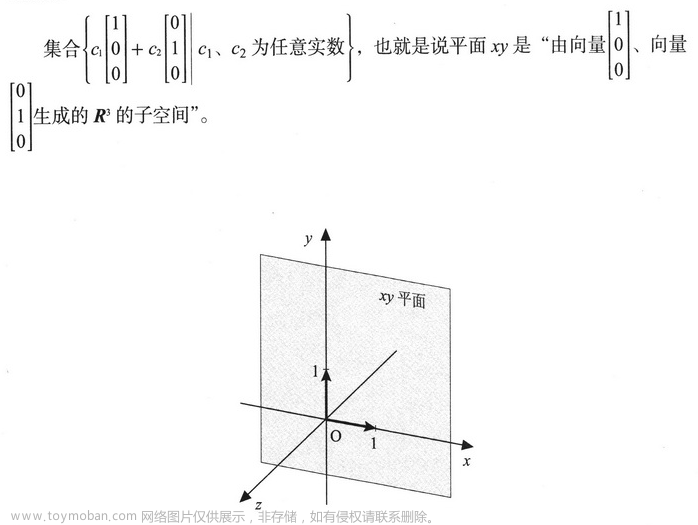
无论什么子空间都必须包含零向量
[
0
0
.
.
.
0
]
\left[ \begin{matrix} 0 \\ 0 \\ .\\ .\\ .\\ 0 \end{matrix} \right]
⎣⎢⎢⎢⎢⎢⎢⎡00...0⎦⎥⎥⎥⎥⎥⎥⎤
3.5.2 基和维数
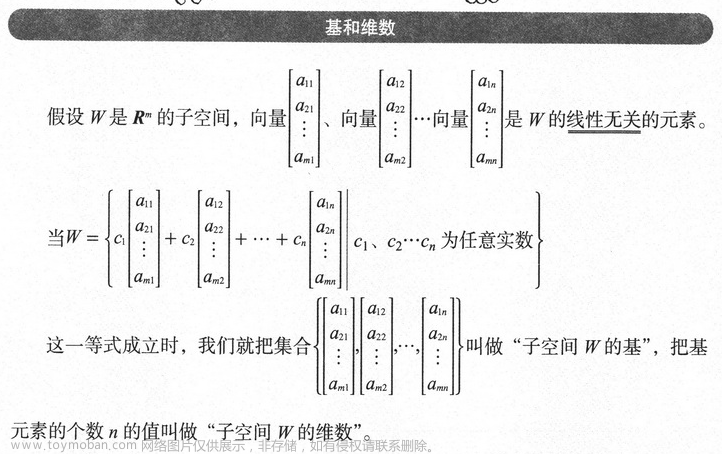
子空间
W
W
W 的维数,一般表示为
d
i
m
W
dimW
dimW,dim 是 dimension 的缩写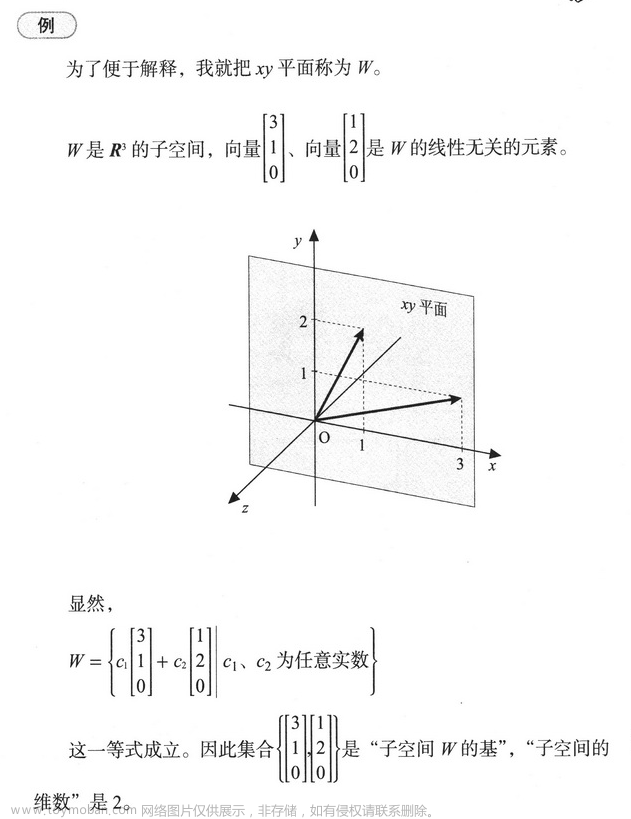
上面子空间由集合
{
[
3
1
0
]
,
[
1
2
0
]
}
\{\left[ \begin{matrix} 3 \\ 1 \\ 0 \end{matrix} \right],\left[ \begin{matrix} 1 \\ 2 \\ 0 \end{matrix} \right]\}
{⎣⎡310⎦⎤,⎣⎡120⎦⎤} 表示 W 的基,基的集合元素是两个,所以子空间的维数是 2。简单来讲,在线性代数中,维数就是基向量个数。
3.6 线性代数中的坐标
线性代数中的“坐标”与一般坐标不一样。一般坐标中是以基
{
[
1
0
.
.
.
0
]
,
[
0
1
.
.
.
0
]
,
.
.
.
,
[
0
0
.
.
.
1
]
}
\{\left[ \begin{matrix} 1 \\ 0 \\ ...\\ 0 \end{matrix} \right],\left[ \begin{matrix} 0 \\ 1 \\ ...\\ 0 \end{matrix} \right],...,\left[ \begin{matrix} 0 \\ 0 \\ ...\\ 1 \end{matrix} \right] \}
{⎣⎢⎢⎡10...0⎦⎥⎥⎤,⎣⎢⎢⎡01...0⎦⎥⎥⎤,...,⎣⎢⎢⎡00...1⎦⎥⎥⎤}为前提来考虑坐标的。
一般坐标中原点和点的关系: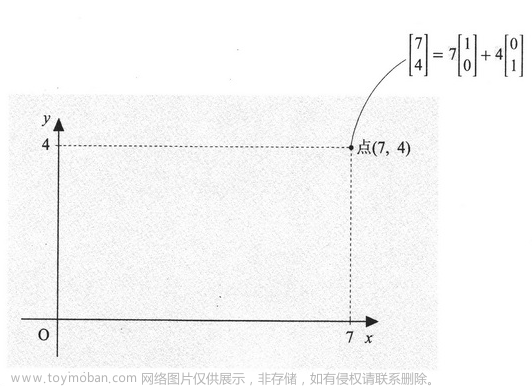
线性代数中基有可能不同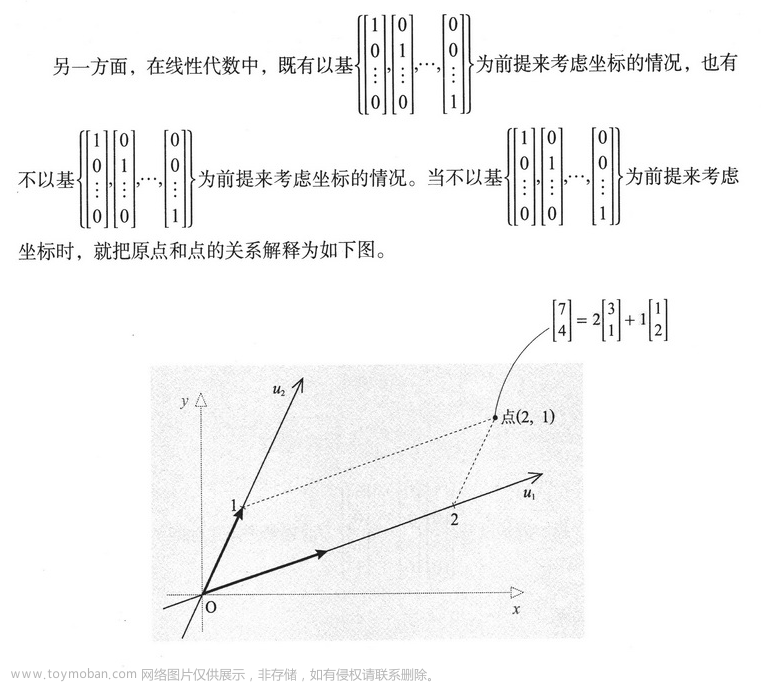
4 线性映射
4.1 线性映射
1.4 节提到过线性映射的定义:
但上面的定义稍显模糊,线性映射完整定义: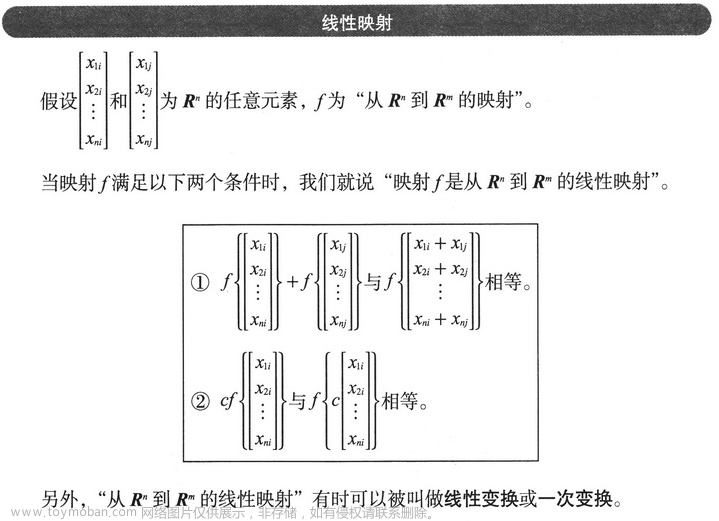
直观地解释就是映射 f 满足这两个条件:1、向量通过 f 由
R
n
R^n
Rn 映射到
R
m
R^m
Rm 之后进行加和等价于向量加和之后,再通过映射 f 由
R
n
R^n
Rn 映射到
R
m
R^m
Rm;2、任意常数乘 f 映射到
R
m
R^m
Rm的向量等价于常数乘向量随后再进行映射
如果映射 f 是从 R n R^n Rn 映射到 R m R^m Rm 的线性映射,那么 f 与 m × n m×n m×n 矩阵意义相同。
证明如下:


从上可以看出,f 相当于 m*n 矩阵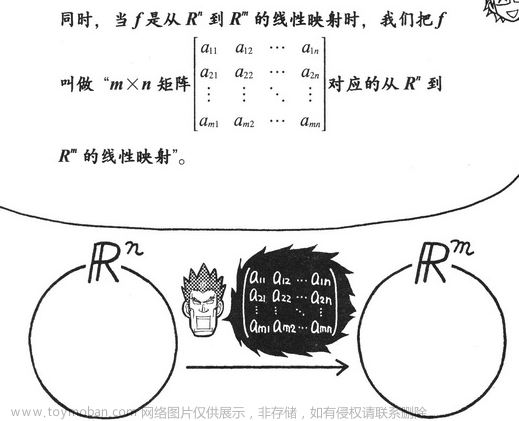
将 n 维向量映射到 m 维上,相当于 m×n 乘 n 维向量,类似于
y
=
A
x
y = Ax
y=Ax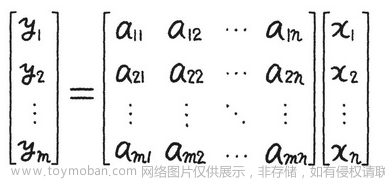
4.2 特殊的线性映射
图中任意一点以
(
x
1
,
x
2
)
(x_1,x_2)
(x1,x2) 表示
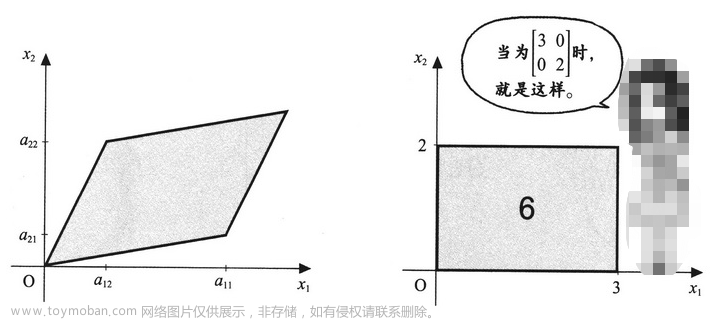
4.2.1 放大
如果把上图沿着 y 轴方向扩展 β 倍,x 轴方向扩展 α 倍,那么扩展后的坐标为:
{
y
1
=
α
x
1
y
2
=
β
x
2
\left\{ \begin{array}{c} y_1=αx_1 \\ y_2=βx_2 \\ \end{array} \right.
{y1=αx1y2=βx2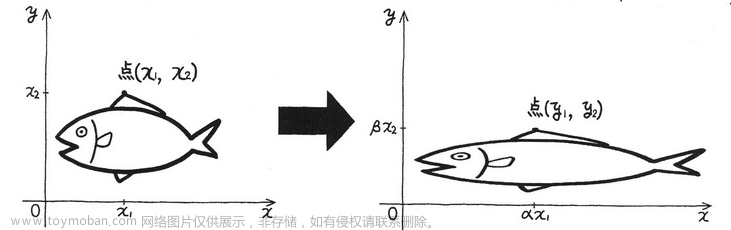
相当于矩阵相乘:
2 阶方阵
[
α
0
0
β
]
\left[ \begin{matrix} α & 0 \\ 0 & β \end{matrix} \right]
[α00β] 对应的就是从
R
2
R^2
R2 到
R
2
R^2
R2 的线性映射
f
f
f。
4.2.2 旋转
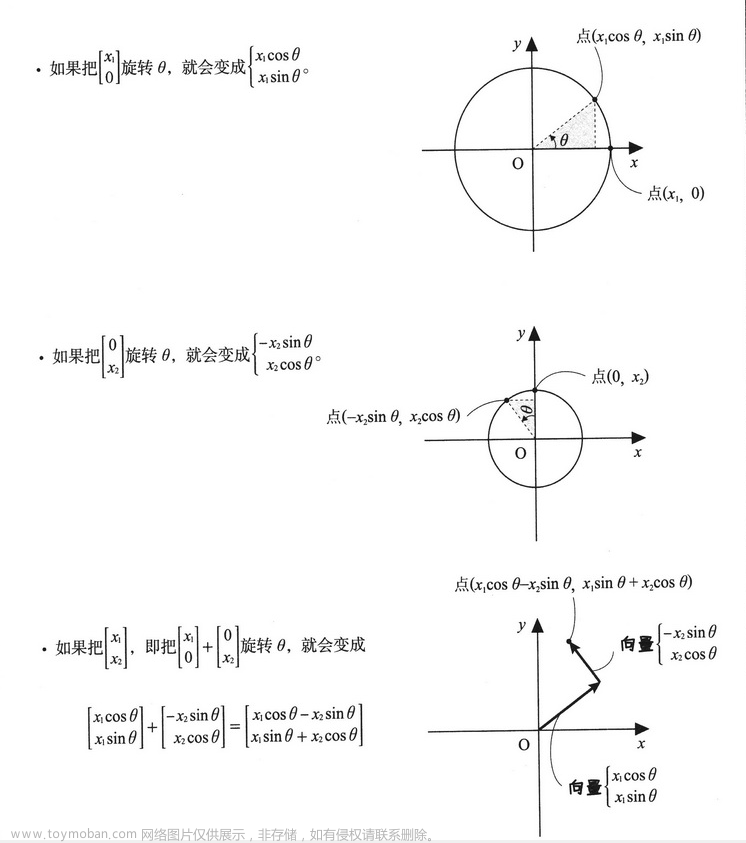
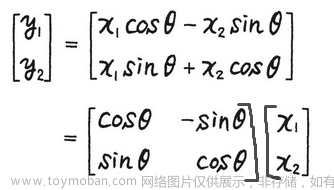
当要把图旋转 θ 时,就可以利用 2 阶方阵
[
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
]
\left[ \begin{matrix} cosθ & -sinθ \\ sinθ & cosθ \end{matrix} \right]
[cosθsinθ−sinθcosθ] 对应的从
R
2
R^2
R2 到
R
2
R^2
R2 的线性映射
f
f
f。
4.2.3 平移
如果把图沿着 x 轴方向平移 b1 单位,沿着 y 轴的方向平移 b2 个单位,那么就有下式:
{
y
1
=
x
1
+
b
1
y
2
=
x
2
+
b
2
\left\{ \begin{array}{c} y_1=x_1 + b_1 \\ y_2=x_2 + b_2\\ \end{array} \right.
{y1=x1+b1y2=x2+b2
也可以写成: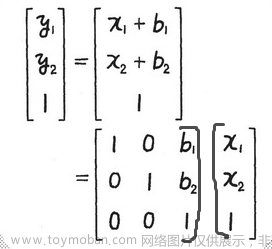
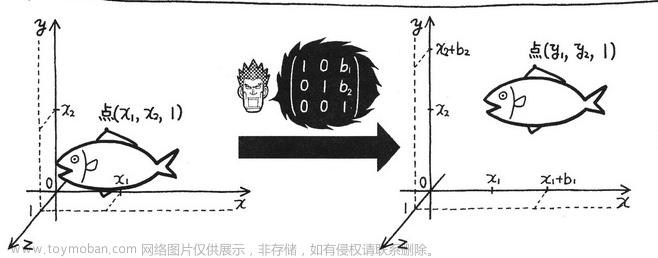
在计算机绘图中,用的通常是 3 维映射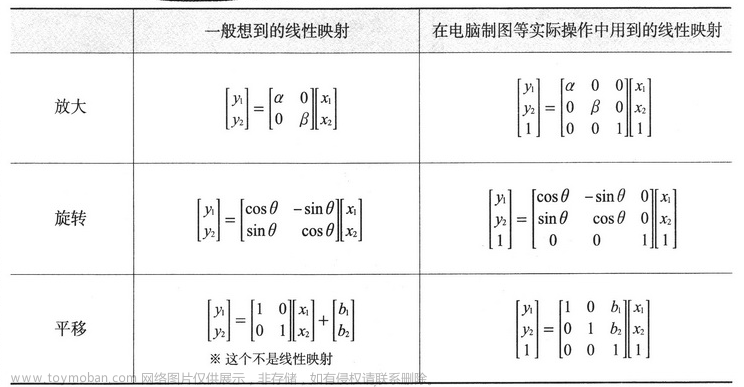
4.2.4 透视投影
透视投影就是通过某一固定观察点与实际物体的直线,将实物 3 维空间的点投影在 2 维平面上的方法。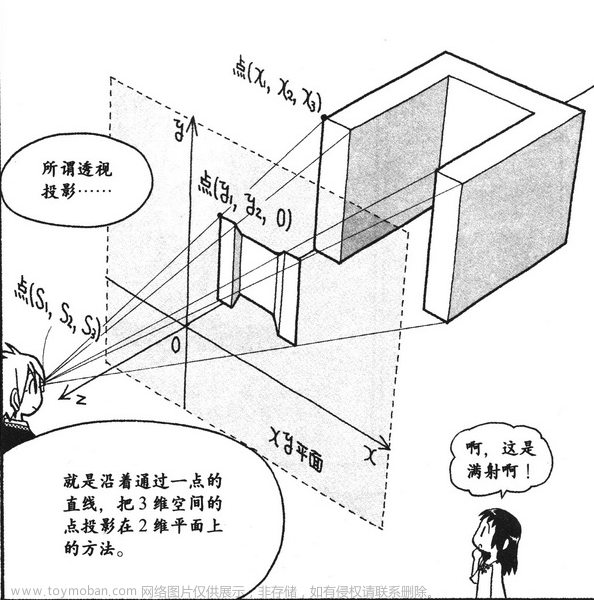
透视投影可以利用 4 阶方阵
4.3 核、像空间、维数公式
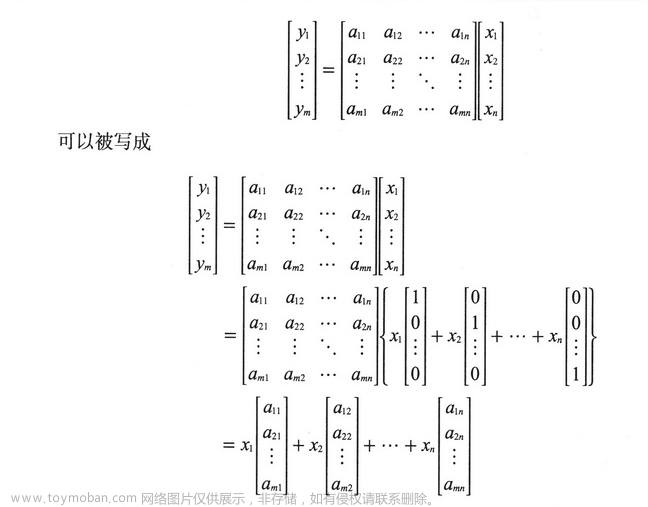
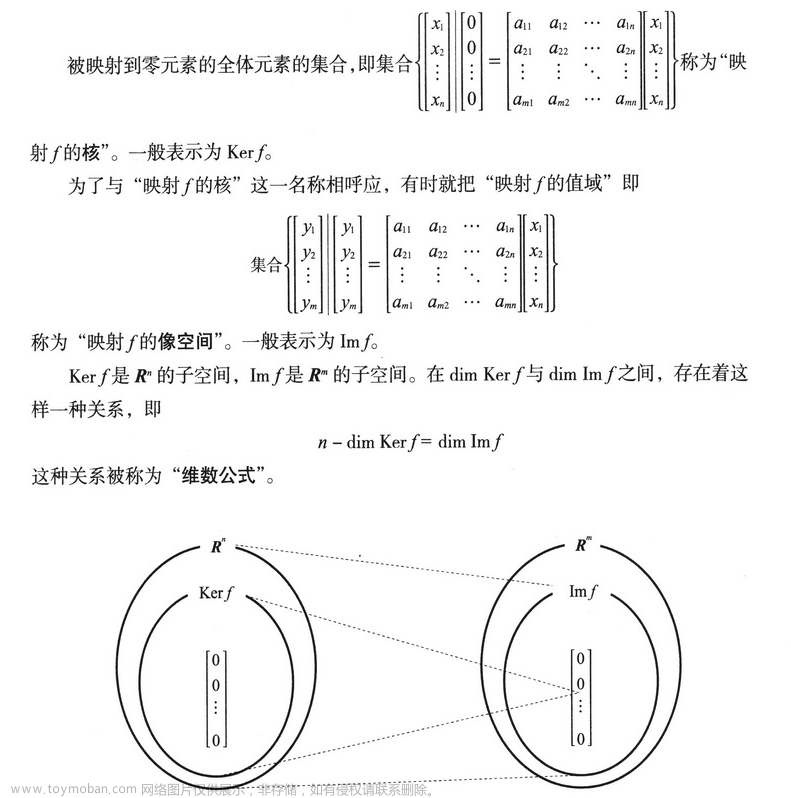


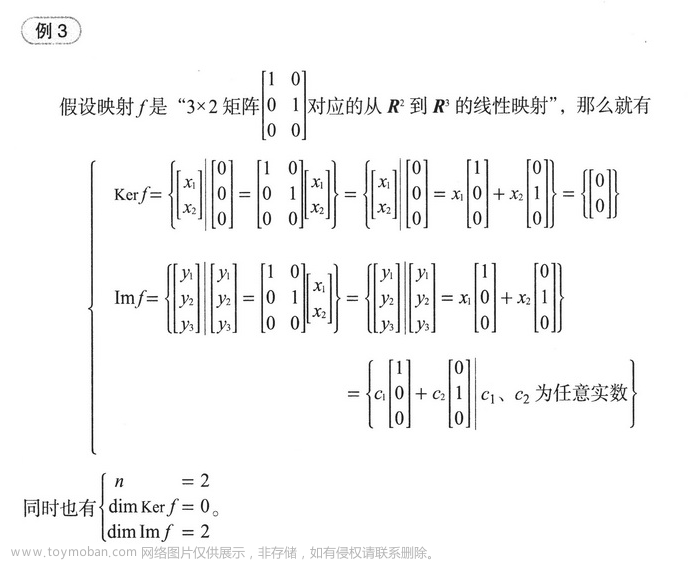

4.4 秩
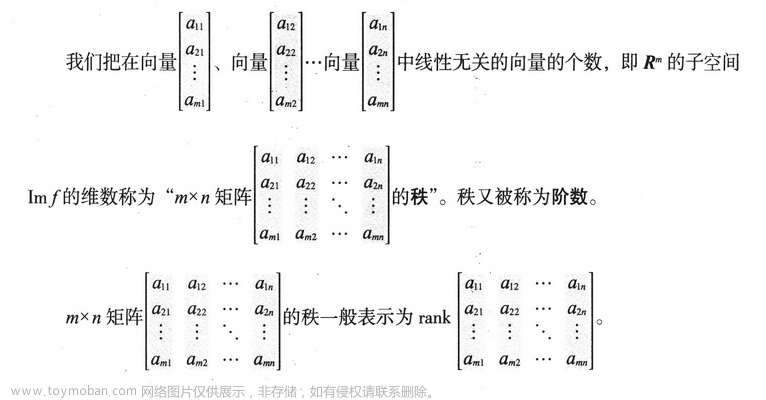
4.5 线性映射与矩阵的关系

5 特征值和特征向量
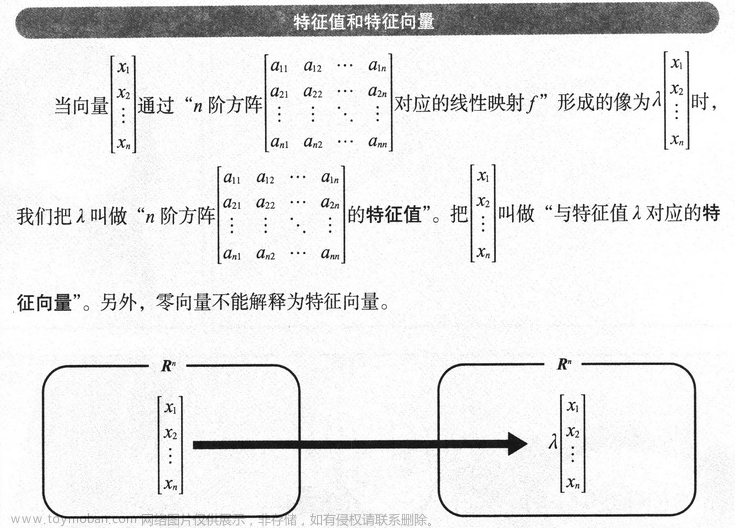
也就是说,在线性代数中,对于一个给定的方阵 A,它的特征向量 v 经过这个线性变换 A 之后,得到的新向量仍然与原来的v 保持在同一条直线上,但其长度或方向也许会改变。即:
拉姆达为其特征值。如果特征值为正,则表示 v 在经过线性变换的作用后方向也不变;如果特征值为负,说明方向会反转;如果特征值为0,则是表示缩回零点。
利用特征值和特征向量求解向量 p 次方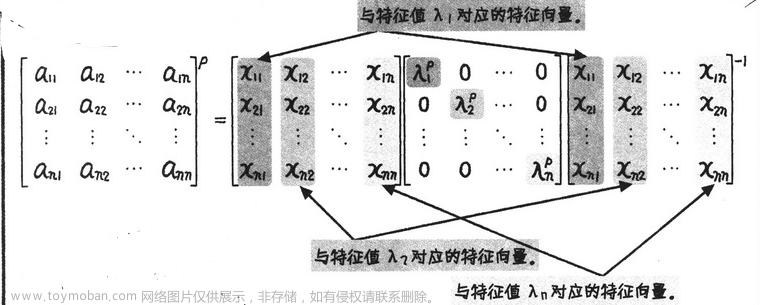
 文章来源:https://www.toymoban.com/news/detail-669317.html
文章来源:https://www.toymoban.com/news/detail-669317.html
参考
史上最全Markdown公式、符号总结!!!
漫画线性代数
特征值和特征向量文章来源地址https://www.toymoban.com/news/detail-669317.html
到了这里,关于轻松掌握线性代数-万字长文基础知识概览的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!