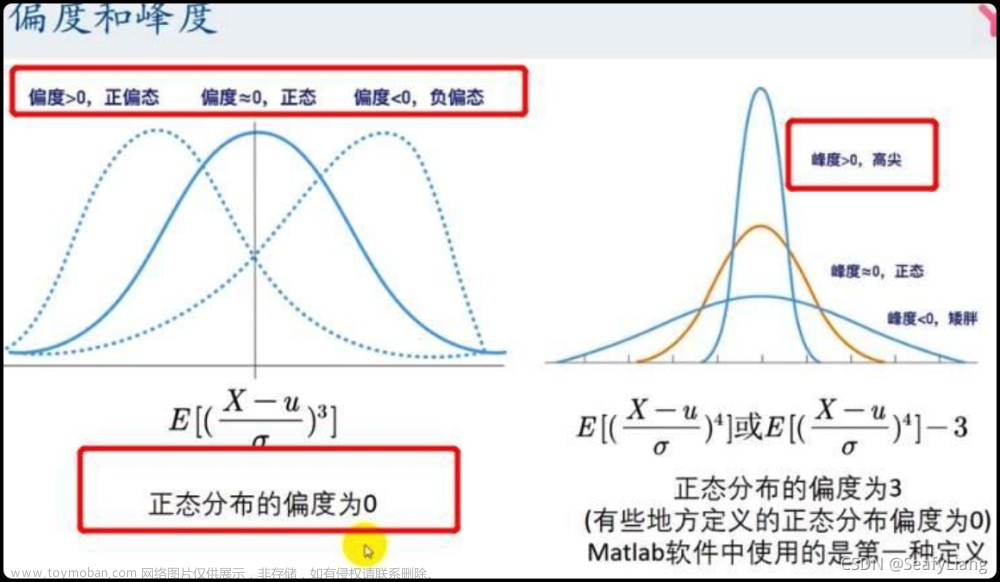
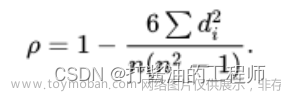肯德尔秩相关系数(Kendall’s Tau)是一种用于衡量两个排列之间相似性的统计指标,它考虑了元素之间的顺序关系而不考虑具体数值。该系数被广泛用于排序、排名和比较不同实验结果的相关性等领域。
具体而言,肯德尔秩相关系数衡量了两个排列之间逆序对(倒置对)的数量,从而反映了它们的相似程度。逆序对是指在一个排列中,两个元素的顺序与另一个排列中它们的顺序相反。肯德尔秩相关系数的计算步骤如下:
-
给定两个排列,比较它们的每一对元素,计算其中一个排列中元素在另一个排列中的顺序关系(逆序或非逆序)。
-
计算逆序对的数量。
-
根据公式计算肯德尔秩相关系数:
τ = Number of concordant pairs − Number of discordant pairs Total number of pairs \tau = \frac{\text{Number of concordant pairs} - \text{Number of discordant pairs}}{\text{Total number of pairs}} τ=Total number of pairsNumber of concordant pairs−Number of discordant pairs
其中,“concordant pairs” 是在两个排列中顺序关系相同的元素对数,而 “discordant pairs” 是顺序关系不同的元素对数。
肯德尔秩相关系数的取值范围在 -1 到 1 之间,具体解释如下:文章来源:https://www.toymoban.com/news/detail-669706.html
- τ = 1 \tau = 1 τ=1:表示两个排列完全一致,没有逆序对。
- τ = − 1 \tau = -1 τ=−1:表示两个排列完全相反,每个元素都是一个逆序对。
- τ = 0 \tau = 0 τ=0:表示两个排列之间没有明显的相关性,逆序对和非逆序对的数量大致相等。
肯德尔秩相关系数具有直观性和易于理解的特点,适用于各种排序和排名场景中,但在某些情况下,它可能对一些特殊关系的敏感性较强。文章来源地址https://www.toymoban.com/news/detail-669706.html
代码
def kendall_tau(arr1, arr2):
if len(arr1) != len(arr2):
raise ValueError("Input arrays must have the same length.")
n = len(arr1)
concordant_pairs = 0
discordant_pairs = 0
for i in range(n - 1):
for j in range(i + 1, n):
# Compare the order of elements in both arrays
if (arr1[i] < arr1[j] and arr2[i] < arr2[j]) or (arr1[i] > arr1[j] and arr2[i] > arr2[j]):
concordant_pairs += 1
elif (arr1[i] < arr1[j] and arr2[i] > arr2[j]) or (arr1[i] > arr1[j] and arr2[i] < arr2[j]):
discordant_pairs += 1
tau = (concordant_pairs - discordant_pairs) / (0.5 * n * (n - 1))
return tau
# Example arrays
arr1 = [1, 2, 3, 4]
arr2 = [2, 1, 4, 3]
# Calculate Kendall's Tau
tau = kendall_tau(arr1, arr2)
print("Kendall's Tau:", tau)
到了这里,关于肯德尔秩相关系数(Kendall‘s Tau)排名的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!