机器学习基础09-审查分类算法（基于印第安糖尿病Pima Indians数据集）-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器学习基础09-审查分类算法（基于印第安糖尿病Pima Indians数据集）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

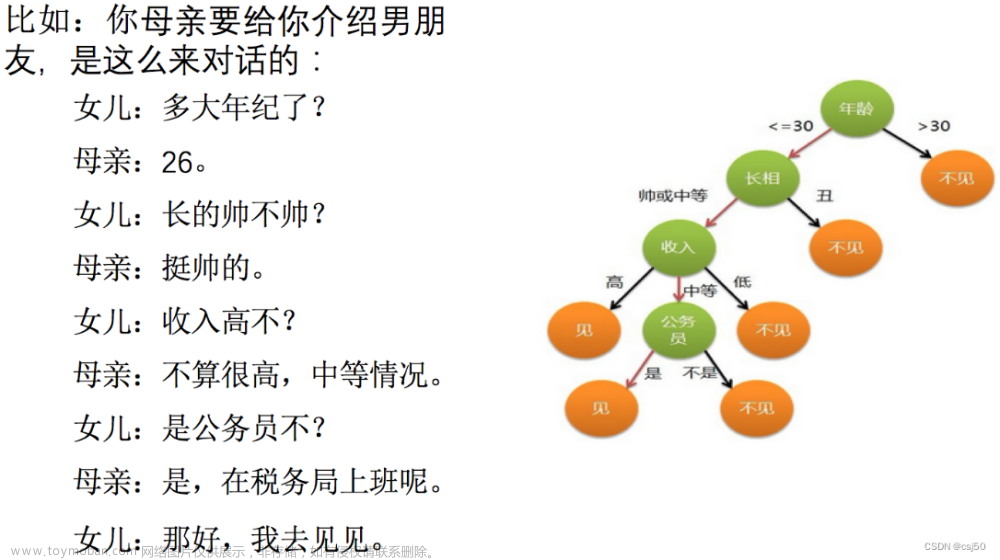
算法审查是选择合适的机器学习算法的主要方法之一。审查算法前并
不知道哪个算法对问题最有效，必须设计一定的实验进行验证，以找到对问题最有效的算法。本章将学习通过
scikit-learn来审查六种机器学习的分类算法，通过比较算法评估矩阵的结果，选择合适的算法。

如何审查机器学习的分类算法？

审查算法前没有办法判断哪个算法对数据集最有效、能够生成最优模
型，必须通过一系列实验判断出哪些算法对问题最有效，然后再进一步来选择算法。这个过程被叫作算法审查。

在选择算法时，应该换一种思路，不是针对数据应该采用哪种算法，而是应该用数据来审查哪些算法。应该先猜测一下，什么算法会具有最好的效果。这是训练我们对数据敏感性的好方法。我非常建议大家对同一个数据集运用不同的算法，来审查算法的有效性，然后找到最有效的算法。
下面是审查算法的几点建议：

尝试多种代表性算法。
尝试多种机器学习的算法。
尝试多种模型。

接下来会介绍几种常见的分类算法。

在分类算法中，目前存在很多类型的分类器：线性分类器、贝叶斯分类器、基于距离的分类器等。接下来会介绍六种分类算法，先介绍两种线性算法：

逻辑回归。
线性判别分析。

再介绍四种非线性算法：

K近邻。
贝叶斯分类器。
分类与回归树。
支持向量机。

下面继续使用Pima Indians数据集来审查算法，同时会采用10折交叉验证来评估算法的准确度。使用平均准确度来标准化算法的得分，以减少数据分布不均衡对算法的影响。

逻辑回归和线性判别分析都是假定输入的数据符合高斯分布。

逻辑回归

回归是一种极易理解的模型，相当于y=f （x），表明自变量x与因变
量y的关系。犹如医生治病时先望、闻、问、切，再判定病人是否生病或生了什么病，此处的“望、闻、问、切”就是获取自变量x，即特征数据；判断是否生病就相当于获取因变量y，即预测分类。

逻辑回归其实是一个分类算法而不是回归算法，通常是利用已知的自变量来预测一个离散型因变量的值（如二进制值0/1、是/否、真/假）。简单来说，它就是通过拟合一个逻辑函数（Logit Function）来预测一个事件发生的概率。所以它预测的是一个概率值，它的输出值应该为 0～1，因此非常适合处理二分类问题。在scikit-learn 中的实现类是LogisticRegression。代码如下：

数据集下载

import pandas as pd

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, cross_val_score

#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)

#打印标签名称
print(data.columns)

#将数据转成数组
array = data.values
#分割数据，去掉最后一个标签
X = array[:, 0:8]

Y = array[:, 8]

num_folds = 10
seed = 7

#特征选择
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
model = LogisticRegression()

result = cross_val_score(model, X, Y, cv=kfold)

print("算法评估结果：%.3f (%.3f)" % (result.mean(), result.std()))

运行结果：

算法评估结果：0.776 (0.045)

线性判别分析

线性判别分析（Linear Discriminant Analysis，LDA），也叫作Fisher线性判别（Fisher Linear
Discriminant，FLD），是模式识别的经典算法，它是在1996年由Belhumeur引入模式识别和人工智能领域的。

线性判别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。

因此，它是一种有效的特征抽取方法。使用这种方法能够使投影后模式样本的类间散布矩阵最大，并且类内散布矩阵最小。就是说，它能够保证投影后模式样本在新的空间中有最小的类内距离和最大的类间距离，即模式在该空间中有最佳的可分离性。线性判别分析与主要成分分析一样，被广泛应用在数据降维中。

在 scikit-learn 中的实现类是LinearDiscriminantAnalysis。代码如下：

import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from sklearn.model_selection import KFold, cross_val_score

#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)

#打印标签名称
print(data.columns)

#将数据转成数组
array = data.values
#分割数据，去掉最后一个标签
X = array[:, 0:8]

Y = array[:, 8]

num_folds = 10
seed = 7

#特征选择
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
model = LinearDiscriminantAnalysis()

result = cross_val_score(model, X, Y, cv=kfold)

print("算法评估结果：%.3f (%.3f)" % (result.mean(), result.std()))

运行结果：

Index(['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin',
       'BMI', 'DiabetesPedigreeFunction', 'Age', 'Outcome'],
      dtype='object')
算法评估结果：0.767 (0.048)

非线性算法

下面介绍四种非线性算法：K近邻（KNN）、贝叶斯分类器、分类与回归树和支持向量机算法。

K近邻算法

K 近邻算法是一种理论上比较成熟的方法，也是最简单的机器学习算法之一。

在KNN中，通过计算对象间距离来作为各个对象之间的非相似性
指标，避免了对象之间的匹配问题，距离一般使用欧氏距离或曼哈顿距离；同时，KNN通过依据k个对象中占优的类别进行决策，而不是通过单一的对象类别决策。这就是 KNN 算法的优势。在 scikit-learn 中的实现类是KNeighborsClassifier。代码如下：

import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from sklearn.model_selection import KFold, cross_val_score
from sklearn.neighbors import KNeighborsClassifier

#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)



#将数据转成数组
array = data.values
#分割数据，去掉最后一个标签
X = array[:, 0:8]

Y = array[:, 8]

num_folds = 10
seed = 7

#特征选择
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
model = KNeighborsClassifier()

result = cross_val_score(model, X, Y, cv=kfold)

print("算法评估结果：%.3f (%.3f)" % (result.mean(), result.std()))

运行结果：


算法评估结果：0.711 (0.051)

贝叶斯分类器

贝叶斯分类器的分类原理是通过某对象的先验概率，利用贝叶斯公式计算出其在所有类别上的后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类。也就是说，贝叶斯分类器是最小错误率意义上的优化。

各个类别出现的概率，哪个最大就认为此待分类项属于哪个类别。贝叶斯分类器的特点如下：

贝叶斯分类器是一种基于统计的分类器，它根据给定样本属于某一个具体类的概率来对其进行分类。
贝叶斯分类器的理论基础是贝叶斯理论。
贝叶斯分类器的一种简单形式是朴素贝叶斯分类器，与随机森林、神经网络等分类器都具有可比的性能。
贝叶斯分类器是一种增量型的分类器。

在贝叶斯分类器中，对输入数据同样做了符合高斯分布的假设。在
scikit-learn中的实现类是GaussianNB。
代码如下：

import pandas as pd

from sklearn.model_selection import KFold, cross_val_score
from sklearn.naive_bayes import GaussianNB


#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)


#将数据转成数组
array = data.values
#分割数据，去掉最后一个标签
X = array[:, 0:8]

Y = array[:, 8]

num_folds = 10
seed = 7

#特征选择
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
#高斯朴素贝叶斯
model = GaussianNB()

result = cross_val_score(model, X, Y, cv=kfold)

print("算法评估结果：%.3f (%.3f)" % (result.mean(), result.std()))

运行结果：

算法评估结果：0.759 (0.039)

分类与回归树

分类与回归树的英文缩写是 CART，也属于一种决策树，树的构建基于基尼指数。

CART假设决策树是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。这样的决策树等价于递归二分每个特征，将输入空间（特征空间）划分为有限个单元，并在这些单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布。

CART算法由以下两步组成。

树的生成：基于训练数据集生成决策树，生成的决策树要尽量大。
树的剪枝：用验证数据集对已生成的树进行剪枝，并选择最优子树，这时以损失函数最小作为剪枝的标准。

决策树的生成就是通过递归构建二叉决策树的过程，对回归树用平方误差最小化准则，或对分类树用基尼指数最小化准则，进行特征选择，生成二叉树。可以通过scikit-learn中的DecisionTreeClassifier类来构建一个CART模型。代码如下：

import pandas as pd

from sklearn.model_selection import KFold, cross_val_score
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier

#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)


#将数据转成数组
array = data.values
#分割数据，去掉最后一个标签
X = array[:, 0:8]

Y = array[:, 8]

num_folds = 10
seed = 7

#特征选择
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
#高斯朴素贝叶斯
model = DecisionTreeClassifier()

result = cross_val_score(model, X, Y, cv=kfold)

print("算法评估结果：%.3f (%.3f)" % (result.mean(), result.std()))

运行结果：

算法评估结果：0.695 (0.051)

支持向量机

支持向量机是Corinna Cortes和Vapnik等于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。

在机器学习中，支持向量机（SVM）是与相关的学习算法有关的监督学习模型，可以分析数据、识别模式，用于分类和回归分析。给定一组训练样本，每条记录标记所属类别，使用支持向量机算法进行训练，并建立一个模型，对新数据实例进行分类，使其成为非概率二元线性分类。

一个SVM模型的例子是，如在空间中的不同点的映射，使得所属不同类别的实例是由一个差距明显且尽可能宽的划分表示。新的实例则映射到相同的空间中，并基于它们落在相同间隙上预测其属于同一个类别。现在SVM也被扩展到处理多分类问题，可以通过scikit-learn中的SVC类来构建一个SVM模型。

代码如下：

import pandas as pd

from sklearn.model_selection import KFold, cross_val_score
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier

#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)


#将数据转成数组
array = data.values
#分割数据，去掉最后一个标签
X = array[:, 0:8]

Y = array[:, 8]

num_folds = 10
seed = 7

#特征选择
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
#高斯朴素贝叶斯
model = SVC()

result = cross_val_score(model, X, Y, cv=kfold)

print("算法评估结果：%.3f (%.3f)" % (result.mean(), result.std()))

算法评估结果：0.760 (0.035)

介绍了六种分类算法，以及它们在 scikit-learn 中的实现。算法主
要分为：线性算法、距离算法、树算法、统计算法等。每一种算法都有不同的适用场景，对数据集有不同的要求。

本次利用 Pima Indians 数据集对这几种算法进行了审查，这是选择合适的算法模型的有效方法。

6个算法评估表如下：文章来源地址https://www.toymoban.com/news/detail-670379.html

算法名称	算法评估结果
逻辑回归LogisticRegression	算法评估结果：0.776 (0.045)
线性判别分析 LinearDiscriminantAnalysis	算法评估结果：0.767 (0.048)
K近邻算法 KNeighborsClassifier	算法评估结果：0.711 (0.051)
贝叶斯分类器GaussianNB	算法评估结果：0.759 (0.039)
分类与回归树DecisionTreeClassifier	算法评估结果：0.695 (0.051)
支持向量机SVC()	算法评估结果：0.760 (0.035)