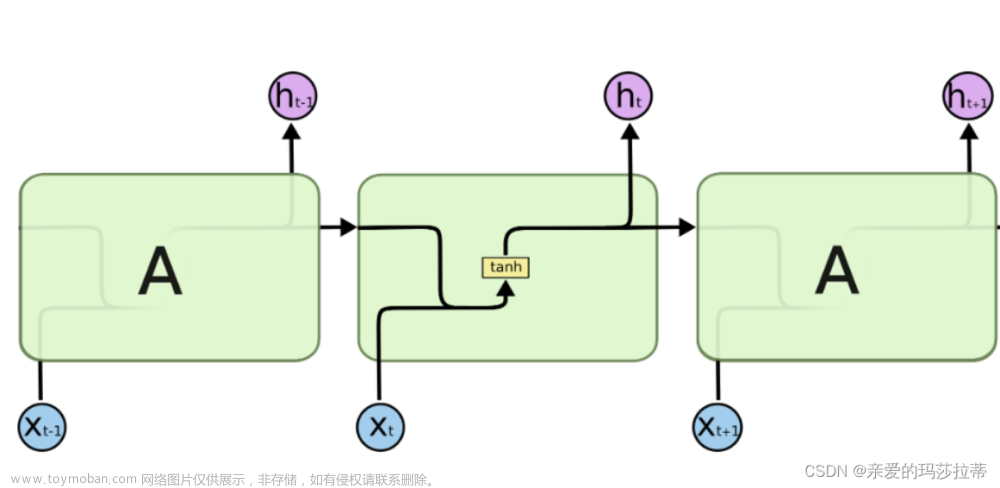
这是史上最简单、清晰,最易读的……
C++语言编写的 带正向传播、反向传播(Forward ……和Back Propagation)……任意Nodes数的人工神经元神经网络……。
大一学生、甚至中学生可以读懂。
适合于,没学过高数的程序员……照猫画虎编写人工智能、深度学习之神经网络,梯度下降……
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
“我在网上看到过很多神经网络的实现方法,但这一篇是最简单、最清晰的。”文章来源:https://www.toymoban.com/news/detail-670433.html
一位来自Umass的华人小哥Along Asong,写了篇神经网络入门教程,在线代码网站Repl.it联合创始人Amjad Masad看完以后,给予如是评价。文章来源地址https://www.toymoban.com/news/detail-670433.html
// c++神经网络手撸20梯度下降22_230820a.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
#include<iostream>
#include<vector>
#include<iomanip> //std::setprecision
#include<sstream> //std::getline std::stof()
using namespace std;
//
float Loss误差损失之和001 = 0.0;
class NN神经网络NN {
private: int inputNode输入层之节点数s, hidden01Node隐藏层01结点数s, hidden22Nodes, outputNode输出层结点数s;
vector<vector<float>> 输入层到第1隐藏层之权重矩阵, 隐藏层1到第二隐藏层2之权重矩阵1to2, 隐藏22到输出层de权重矩阵; //这些变量为矩阵
vector<float> 隐藏层1偏置1, 隐藏层2偏置2, O输出偏置o;
vector<float>隐藏层1数据1, 隐藏层2数据2, 输出数据output;
void initLayer每一层的WeightsAndBiases(vector<vector<float>>& weights权重, vector<float>& biases偏置)
{
for (size_t i = 0; i < weights权重.size(); ++i) {//for110i
for (size_t j = 0; j < weights权重[0].size(); ++j) { weights权重[i][j] = ((rand() % 2) - 1) / 1.0; }
biases偏置[i] = ((rand() % 2) - 1) / 1.0;
}//for110i
}//void initLayerWeightsAndBiases(
void initWeightsAndBiases初始化权重和偏置矩阵() {
initLayer每一层的WeightsAndBiases(输入层到第1隐藏层之权重矩阵, 隐藏层1偏置1);
initLayer每一层的WeightsAndBiases(隐藏层1到第二隐藏层2之权重矩阵1to2, 隐藏层2偏置2);
initLayer每一层的WeightsAndBiases(隐藏22到输出层de权重矩阵 , O输出偏置o);
}
//激活函数-激活的过程
vector<float> activate(const vector<float>& inputs, const vector< vector<float>>& weights, const vector<float>& biases) {
vector<float> layer_output(weights.size(), 0.0);
for (size_t i = 0; i < weights.size(); i++) {
for (size_t j = 0; j < inputs.size(); j++) {
layer_output[i] += inputs[j] * weights[i][j];
}//for220j
layer_output[i] += biases[i];
layer_output[i] = sigmoid(layer_output[i]);
}//for110i
return layer_output;
}//vector<float> activate
//subtract求差:两个 向量的差
std::vector<float> subtract(const std::vector<float>& a, const std::vector<float>& b) {
std::vector<float> result(a.size(), 0.0);
for (size_t i = 0; i < a.size(); i++) {
result[i] = a[i] - b[i];
}
return result;
}//vector<float>subtract
//dotT点乘
std::vector<float> dotT(const std::vector<float>& a, const std::vector<std::vector<float>>& b) {
std::vector<float> result(b[0].size(), 0.0);
for (size_t i = 0; i < b[0].size(); i++) {
for (size_t j = 0; j < a.size(); j++) {
result[i] += a[j] * b[j][i];
}
}
return result;
}
//更新权重矩阵s(们), 和偏置(向量)S们
void updateWeights(const std::vector<float>& inputs, const std::vector<float>& errors, const std::vector<float>& outputs,
std::vector<std::vector<float>>& weights, std::vector<float>& biases, float lr) {
for (size_t i = 0; i < weights.size(); i++) {
for (size_t j = 0; j < weights[0].size(); j++) {
weights[i][j] += lr * errors[i] * sigmoid导函数prime(outputs[i]) * inputs[j];
}
biases[i] += lr * errors[i] * sigmoid导函数prime(outputs[i]);
}
}//void updateWeights(
public:
NN神经网络NN(int inputNode输入层之节点数s, int hidden01Node隐藏层01结点数s, int hidden22Nodes, int outputNode输出层结点数s)
:inputNode输入层之节点数s(inputNode输入层之节点数s), hidden01Node隐藏层01结点数s(hidden01Node隐藏层01结点数s), hidden22Nodes(hidden22Nodes), outputNode输出层结点数s(outputNode输出层结点数s)
{
srand(time(NULL));
//初始换权重矩阵
输入层到第1隐藏层之权重矩阵.resize(hidden01Node隐藏层01结点数s, vector<float>(inputNode输入层之节点数s));
隐藏层1到第二隐藏层2之权重矩阵1to2.resize(hidden22Nodes, vector<float>(hidden01Node隐藏层01结点数s));
隐藏22到输出层de权重矩阵.resize(outputNode输出层结点数s, vector<float>(hidden22Nodes));//
隐藏层1偏置1.resize(hidden01Node隐藏层01结点数s);
隐藏层2偏置2.resize(hidden22Nodes);
O输出偏置o.resize(outputNode输出层结点数s);
initWeightsAndBiases初始化权重和偏置矩阵();
}//NN神经网络NN(i
//sigmoid激活函数及导数
float sigmoid(float x){ return 1.0 / (1.0 + exp(-x)); }
float sigmoid导函数prime(float x) { return x * (1 - x); }
//Forward前向传播
vector<float> predict(const vector<float>& input输入数据) {
//用激活函数sigmoid-激活的过程
隐藏层1数据1 = activate(input输入数据, 输入层到第1隐藏层之权重矩阵, 隐藏层1偏置1); //激活函数
// 第一隐藏层到第二隐藏层
隐藏层2数据2 = activate(隐藏层1数据1, 隐藏层1到第二隐藏层2之权重矩阵1to2, 隐藏层2偏置2);//hidden1, wh1h2, bias_h2);
// 第二隐藏层到输出层
输出数据output = activate(隐藏层2数据2, 隐藏22到输出层de权重矩阵, O输出偏置o);// , wh2o, bias_o);
return 输出数据output;
}//vector<float>predict(
// 反向传播//Backpropagation
void train(const vector<float>& inputs, const vector<float>& target目标数据s, float lr学习率) {
vector<float> output尝试的输出数据s = predict(inputs);
// 输出层误差
vector<float> output_error输出误差s = subtract(target目标数据s, output尝试的输出数据s);//
Loss误差损失之和001 = 0.0;
for (int ii = 0; ii < outputNode输出层结点数s; ++ii) { Loss误差损失之和001 += fabs(output_error输出误差s[ii]); }
//=========================================================================
// 隐藏层2误差
vector<float> hidden2_errors = dotT(output_error输出误差s, 隐藏22到输出层de权重矩阵);
// 隐藏层1误差
vector<float> hidden1_errors = dotT(hidden2_errors, 隐藏层1到第二隐藏层2之权重矩阵1to2);
// 更新权重: 隐藏层2到输出层(的权重矩阵
updateWeights(隐藏层2数据2, output_error输出误差s, output尝试的输出数据s, 隐藏22到输出层de权重矩阵, O输出偏置o, lr学习率);
// 更新权重: 隐藏层1到隐藏层2
updateWeights(隐藏层1数据1, hidden2_errors, 隐藏层2数据2, 隐藏层1到第二隐藏层2之权重矩阵1to2, 隐藏层2偏置2, lr学习率);
// 更新权重: 输入层到隐藏层1的权重矩阵)
updateWeights(inputs, hidden1_errors, 隐藏层1数据1, 输入层到第1隐藏层之权重矩阵, 隐藏层1偏置1, lr学习率);
}// void train(
// // 反向传播//Backpropagation
};//class NN神经网络NN {
#define Num训练数据的个数s 5
int main()
{
NN神经网络NN nn(9, 11, 4, 2);// 11, 10, 4);
// Example
int 训练数据的个数s = Num训练数据的个数s;
std::vector<float> input[Num训练数据的个数s];
/* input[0] = {0,1,0, 0,1,0, 0,1,0}; //1“竖线”或 “1”字{ 1.0, 0.5, 0.25, 0.125 };
input[1] = { 0,0,0, 1,1,1,0,0,0 }; //-“横线”或 “-”减号{ 1.0, 0.5, 0.25, 0.125 };
input[2] = { 0,1,0, 1,1,1, 0,1,0 }; //+“+”加号{ 1.0, 0.5, 0.25, 0.125 };
input[3] = { 0,1,0, 0,1.2, 0, 0,1, 0 }; // '1'或 '|'字型{ 1.0, 0.5, 0.25, 0.125 };
input[4] = { 1,1,0, 1,0,1.2, 1,1,1 }; //“口”字型+{ 1.0, 0.5, 0.25, 0.125 };
std::vector<float> target[Num训练数据的个数s];
target[0] = { 1.0, 0,0,0 };// , 0};//1 , 0}; //0.0, 1.0, 0.5}; //{ 0.0, 1.0 };
target[1] = { 0, 1.0 ,0,0 };// , 0};//- 91.0, 0};// , 0, 0}; //
target[2] = { 0,0,1.0,0 };// , 0};//+ 1.0, 0.5};
target[3] = { 1.0 ,0,0, 0.5 };// , 0}; //1
target[4] = { 0,0,0,0 };// , 1.0}; //“口”
*/
vector<float> target[Num训练数据的个数s];
input[0] = { 0,0,0, 1,1,1, 0,0,0 }; target[0] = { 0, 1 }; //"-"
input[1] = { 0,1,0, 0,1,0, 0,1,0 }; target[1] = { 1.0, 0 };
input[2] = { 1,1,1, 0,0,0, 0,0,0 }; target[2] = { 0, 0.5 };
input[3] = { 0,0,1, 0,0,1, 0,0,1 }; target[3] = { 0.9, 0 };
for (int i = 0; i < 50000; ++i) {//for110i
for (int jj = 0; jj < Num训练数据的个数s - 1; ++jj) {
//for (auto& val: input ) {
nn.train(input[jj], target[jj], 0.001);
if (0 ==i % 10000) { cout << "[Lost:" << Loss误差损失之和001 << endl; }
}//for220jj
}//for110i
cout << endl;
//--------------------------------------
input[1] = { 0,0,0, 1,1, 0.98, 0,0,0 }; //1/
std::vector<float> outpu输出数据001t = nn.predict(input[0]);
for (auto& val : outpu输出数据001t)
std::cout << std::fixed << std::setprecision(9) << val << " ";
cout << endl;
//-------------------------------------------------------------
std::string str0001;
do {
std::cout << std::endl << "请输入一个字符串(要求字符串是包含9个由逗号分隔的数字的字符串,如 1,2,0,0,5,0,0,8,9等): " << std::endl;
std::getline(std::cin, str0001);
std::stringstream s01s001(str0001);
for (int i = 0; i < 9; ++i) {
std::string temp;
std::getline(s01s001, temp, ',');
input[1][i] = (float)std::stof(temp); // 将字符串转化为整数
}
std::cout << "数字数组为: ";
for (int i = 0; i < 9; ++i) {
std::cout << input[1][i] << " ";
}
outpu输出数据001t = nn.predict(input[1]);
std::cout << std::endl;
for (auto& val : outpu输出数据001t)
std::cout << std::fixed << std::setprecision(9) << val << " ";
} while (true);// 1 == 1);
//======================================
cout << "Hello World!\n";
}//到了这里,关于C++最易读手撸神经网络两隐藏层(任意Nodes每层)梯度下降230820a的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!