一.图的定义和分类
1.通俗定义
图是由一组顶点和一组能够将两个顶点连接的边组成的。
2.图的分类
按照连接两个顶点的边的不同，可以把图分为以下两种：
无向图：边仅仅连接两个顶点，没有其他含义；
有向图：边不仅连接两个顶点，并且具有方向;
另外图还可以分为赋权图和非赋权图，一个是每条边都带有权值，一个是每条边都没有权值。
通常权值是具有某种实际意义的数，比如2个顶点之间的距离，耗费等。
综上图可以大致分为无向图，有向图，赋权无向图，赋权有向图四种。
注：一般情况下，图中两个顶点只有一条边连接。
3.数学定义
4.图的相关概念
相邻顶点：
当两个顶点通过一条边相连时，我们称这两个顶点是相邻的，并且称这个边依赖于这两个顶点。
度 出度 入度：
某个顶点的度就是依附于该顶点的边的个数。
子图：
是一幅图的所有边的子集（包含这些边依附的顶点）组成的图。
路径：
是由边顺序连接的一系列的顶点组成。
环：
是一条至少含有一条边且终点和起点相同的路径。
连通图：
如果图中任一一个顶点都存在一条路径到达另外一个顶点，那么这幅图就称之为联通图。
连通子图：
一个非联通图由若干连通的部分组成，每一个连通的部分都可以成为该图的连通子图。
连通分量:
连通子图的数量
完全图/简单完全图:
假设一个图有n个顶点，那么如果任意两个顶点之间都有边的话，该图就称为完全图。
n个端点的完全无向图有n(n−1)/2条边，而完全有向图有n(n-1)条边。【相当于之前每两个点之间只有一条边，现在有一来一去两条边】
二.图的存储结构
要表示一幅图，只需要表示清楚一下两部分内容即可：
1.图中所有的顶点；
2.所有连接顶点的边；
一般的话我们只需要清楚点的个数，然后存储好边的信息就够了。
常见图(更准确的说是边)的存储结构有两种：邻接矩阵和邻接表
【1】邻接矩阵
1.使用一个V*V的二维数组int[V][V] adj。
2.无向图如果顶点v和顶点w相连，我们只需要把adj[v][w]和adj[w][v]的值设置为1，否则设置为0即可。
有向图v->w，把adj[v][w]的值设置为1，w->v,把adj[w][v]的值设置为1。
3.如果是赋权图的话直接将值换为对应的权值即可。
很明显，邻接矩阵这种存储方式的空间复杂度是V^2的，如果我们处理的问题规模比较大的话，内存空间极有可能不够用。
【2】邻接表
1.使用一个大小为V的数组Queue[V] adj，把索引看做是顶点；
2.无向图每个索引处adj[v]存储了一个链表，该链表中存储的是所有与该顶点相邻的其他顶点
有向图的话一般使用的是逆转链表，简单说就是每个结点存储以这个点为终点的单链表。
上图表示的意思是1连接4,3,2;而2连接1,5;而3连接1,5;而4连接1,5;而5连接4,3,2。
很明显，邻接表的空间并不是是线性级别的，所以后面我们一直采用邻接表这种存储形式来表示图。
三.图的搜索
1.深度优先搜索
所谓的深度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，然后找兄弟结点。
一般是先序遍历，即根结点 ---> 左子树 ---> 右子树。
复杂度：用邻接矩阵实现复杂度为O(n的平方)，用邻接表实现的时间复杂度为O(n+e)【n是点的个数，e是边的个数】
例：
2.广度优先搜索
所谓的广度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，然后找子结点。
需要注意的是，图的广度优先搜索和树一样，如果找完兄弟节点后，要返回刚开始的结点，去寻找其子结点。
复杂度：用邻接矩阵实现复杂度为O(n的平方)，用邻接表实现的时间复杂度为O(n+e)【n是点的个数，e是边的个数】
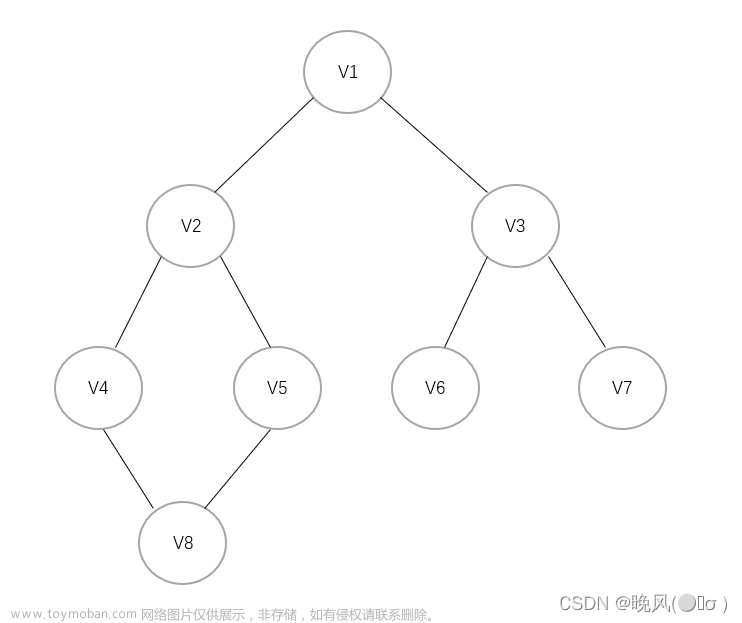
例：下面这道题选择D文章来源：https://www.toymoban.com/news/detail-670515.html
文章来源地址https://www.toymoban.com/news/detail-670515.html
到了这里，关于算法与数据结构（十）--图的入门的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
