排序算法：插入排序-Toy模板网

这篇具有很好参考价值的文章主要介绍了排序算法：插入排序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

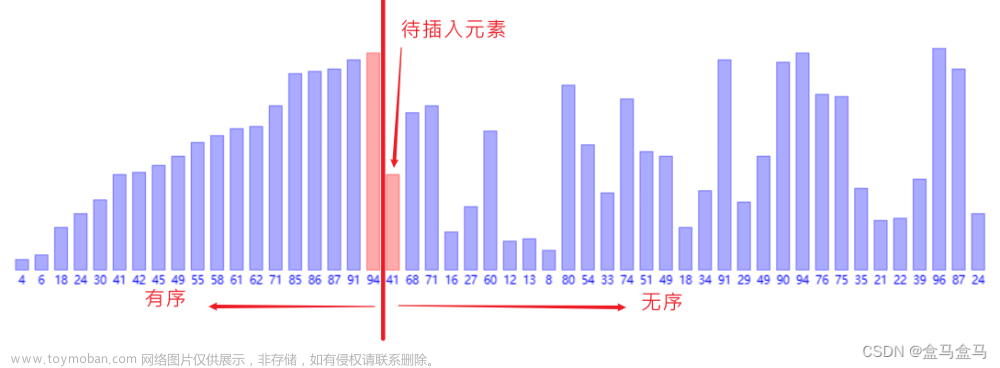
插入排序的思想非常简单，生活中有一个很常见的场景：在打扑克牌时，我们一边抓牌一边给扑克牌排序，每次摸一张牌，就将它插入手上已有的牌中合适的位置，逐渐完成整个排序。

插入排序有两种写法：

交换法：在新数字插入过程中，不断与前面的数字交换，直到找到自己合适的位置。
移动法：在新数字插入过程中，与前面的数字不断比较，前面的数字不断向后挪出位置，当新数字找到自己的位置后，插入一次即可。

交换法插入排序

public static void insertSort(int[] arr) {
    // 从第二个数开始，往前插入数字
    for (int i = 1; i < arr.length; i++) {
        // j 记录当前数字下标
        int j = i;
        // 当前数字比前一个数字小，则将当前数字与前一个数字交换
        while (j >= 1 && arr[j] < arr[j - 1]) {
            swap(arr, j, j - 1);
            // 更新当前数字下标
            j--;
        }
    }
}
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

当数字少于两个时，不存在排序问题，当然也不需要插入，所以我们直接从第二个数字开始往前插入。

整个过程就像是已经有一些数字坐成了一排，这时一个新的数字要加入，这个新加入的数字原本坐在这一排数字的最后一位，然后它不断地与前面的数字比较，如果前面的数字比它大，它就和前面的数字交换位置。

移动法插入排序

我们发现，在交换法插入排序中，每次交换数字时，swap 函数都会进行三次赋值操作。但实际上，新插入的这个数字并不一定适合与它交换的数字所在的位置。也就是说，它刚换到新的位置上不久，下一次比较后，如果又需要交换，它马上又会被换到前一个数字的位置。

由此，我们可以想到一种优化方案：让新插入的数字先进行比较，前面比它大的数字不断向后移动，直到找到适合这个新数字的位置后，新数字只做一次插入操作即可。

这种方案我们需要把新插入的数字暂存起来，代码如下：

public static void insertSort(int[] arr) {
    // 从第二个数开始，往前插入数字
    for (int i = 1; i < arr.length; i++) {
        int currentNumber = arr[i];
        int j = i - 1;
        // 寻找插入位置的过程中，不断地将比 currentNumber 大的数字向后挪
        while (j >= 0 && currentNumber < arr[j]) {
            arr[j + 1] = arr[j];
            j--;
        }
        // 两种情况会跳出循环：1. 遇到一个小于或等于 currentNumber 的数字，跳出循环，currentNumber 就坐到它后面。
        // 2. 已经走到数列头部，仍然没有遇到小于或等于 currentNumber 的数字，也会跳出循环，此时 j 等于 -1，currentNumber 就坐到数列头部。
        arr[j + 1] = currentNumber;
    }
}

整个过程就像是已经有一些数字坐成了一排，这时一个新的数字要加入，所以这一排数字不断地向后腾出位置，当新的数字找到自己合适的位置后，就可以直接坐下了。重复此过程，直到排序结束。

时间复杂度 & 空间复杂度

插入排序过程需要两层循环，时间复杂度为O(n²)；只需要常量级的临时变量，空间复杂度为 O(1)。

LC 912.排序数组

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]文章来源地址https://www.toymoban.com/news/detail-670561.html

class Solution {
    public int[] sortArray(int[] nums) {
        int max = nums[0];
        int min = nums[0];
        for (int i = 1; i < nums.length; i++) {
            if (max < nums[i]) {
                max = nums[i];
            } else if (min > nums[i]) {
                min = nums[i];
            }
        }
        int[] count = new int[max - min + 1];
        for (int v : nums) {
            count[v - min]++;
        }
        int k = 0;
        for (int i = 0; i < count.length; i++) {
            while (count[i] > 0) {
                nums[k++] = i + min;
                count[i]--;
            }
        }
        return nums;
    }
}

到了这里，关于排序算法：插入排序的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！