基于opencv的SVD分解求解变换矩阵-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于opencv的SVD分解求解变换矩阵。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

基于opencv的SVD分解求解变换矩阵

一、坐标转换关系

在机器视觉领域，坐标系之间的转换是必不可少的。空间坐标转换的实质是用公共点的两套坐标去推导出两个坐标系之间的转换关系：R（旋转矩阵）和T（平移向量）。

opencv svdecomp,三维测量,opencv,计算机视觉

二、算法原理

其实点云的配准过程就是求解旋转矩阵R和平移向量T，这里记目标函数为：
opencv svdecomp,三维测量,opencv,计算机视觉
式中，n是匹配点个数，假设其最小二乘解为R’和T’，那么

和Q的质心相同（最小二乘法的原理决定的），其中：
opencv svdecomp,三维测量,opencv,计算机视觉
而P的质心为：

opencv svdecomp,三维测量,opencv,计算机视觉
接着使：

这时目标函数可以改写为：

分解：

求导，则有：

上式中H为三阶方阵：

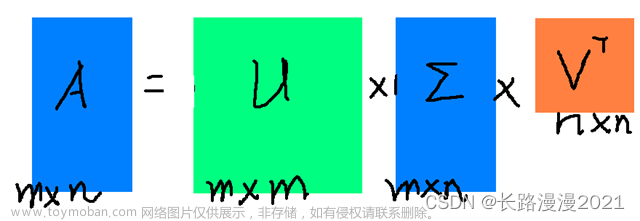
用SVD分解H矩阵有：

令X=VUT，则有：

opencv svdecomp,三维测量,opencv,计算机视觉
由此可见XH为对称正定矩阵，所以对任意的三阶正交方阵B有tr(XH)≥tr(BXH)，则对于所有的三阶正交方阵中，只有当X的行列式接近于1或者等于1时，则旋转矩阵R=X。那么平移矩阵为：
文章来源地址https://www.toymoban.com/news/detail-670643.html

三、代码实现

//SVD计算坐标转换，输入为公共点在两个坐标系的坐标，输出为旋转矩阵和平移向量
void GetRigidTrans3D(cv::Point3f* srcPoints, cv::Point3f* dstPoints, int pointsNum, TRigidTrans3D& transform)
{
	double srcSumX = 0.0f;
	double srcSumY = 0.0f;	
	double srcSumZ = 0.0f;	
	double dstSumX = 0.0f;	
	double dstSumY = 0.0f;	
	double dstSumZ = 0.0f;	
	//计算质心	
	for (int i = 0; i < pointsNum; ++i)	
	{		
		srcSumX += srcPoints[i].x;		
		srcSumY += srcPoints[i].y;		
		srcSumZ += srcPoints[i].z;		
		dstSumX += dstPoints[i].x;		
		dstSumY += dstPoints[i].y;		
		dstSumZ += dstPoints[i].z;			
	}	
	cv::Point3f centerSrc, centerDst;	
	centerSrc.x = float(srcSumX / pointsNum);	
	centerSrc.y = float(srcSumY / pointsNum);	
	centerSrc.z = float(srcSumZ / pointsNum);	
	centerDst.x = float(dstSumX / pointsNum);	
	centerDst.y = float(dstSumY / pointsNum);	
	centerDst.z = float(dstSumZ / pointsNum);	
	cv::Mat srcMat(3, pointsNum, CV_32FC1);	
	cv::Mat dstMat(3, pointsNum, CV_32FC1);	
	float* srcDat = (float*)(srcMat.data);	
	float* dstDat = (float*)(dstMat.data);	
	for (int i = 0; i < pointsNum; ++i)	
	{	
		srcDat[i] = srcPoints[i].x - centerSrc.x;
		srcDat[pointsNum + i] = srcPoints[i].y - centerSrc.y;		
		srcDat[pointsNum * 2 + i] = srcPoints[i].z - centerSrc.z;
		dstDat[i] = dstPoints[i].x - centerDst.x;		
		dstDat[pointsNum + i] = dstPoints[i].y - centerDst.y;		
		dstDat[pointsNum * 2 + i] = dstPoints[i].z - centerDst.z;
	}
	//SVD分解	
	cv::Mat matS = srcMat * dstMat.t();	
	cv::Mat matU, matW, matV;	
	cv::SVDecomp(matS, matW, matU, matV);	
	cv::Mat matTemp = matU * matV;	
	double det = cv::determinant(matTemp);	
	float datM[] = { 1, 0, 0, 0, 1, 0, 0, 0, det };	
	cv::Mat matM(3, 3, CV_64FC1, datM);	
	cv::Mat matR = matV.t() * matM * matU.t();	
	transform.matR[0] = matR.at<float>(0, 0);	
	transform.matR[1] = matR.at<float>(0, 1);	
	transform.matR[2] = matR.at<float>(0, 2);	
	transform.matR[3] = matR.at<float>(1, 0);	
	transform.matR[4] = matR.at<float>(1, 1);	
	transform.matR[5] = matR.at<float>(1, 2);	
	transform.matR[6] = matR.at<float>(2, 0);	
	transform.matR[7] = matR.at<float>(2, 1);	
	transform.matR[8] = matR.at<float>(2, 2); 	
	double* datR = (double*)(transform.matR);	
	transform.X = centerDst.x - (centerSrc.x * datR[0] + centerSrc.y * datR[1] + centerSrc.z * datR[2]);	
	transform.Y = centerDst.y - (centerSrc.x * datR[3] + centerSrc.y * datR[4] + centerSrc.z * datR[5]);	
	transform.Z = centerDst.z - (centerSrc.x * datR[6] + centerSrc.y * datR[7] + centerSrc.z * datR[8]); 
}