【Spring Boot】什么是深度优先遍历与广度优先遍历？用Spring Boot项目举例说明。-Toy模板网

这篇具有很好参考价值的文章主要介绍了【Spring Boot】什么是深度优先遍历与广度优先遍历？用Spring Boot项目举例说明。。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

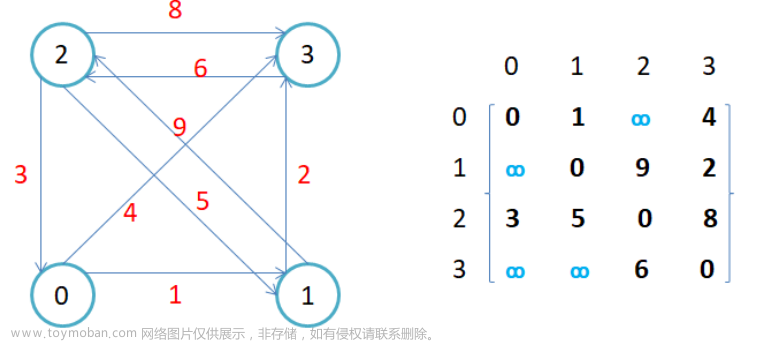
深度优先遍历（Depth First Search，DFS）和广度优先遍历（Breadth First Search，BFS）是图的遍历算法。其中，深度优先遍历从某个起始点开始，先访问一个节点，然后跳到它的一个相邻节点继续遍历，直到没有未遍历的节点，此时回溯到上一个节点，继续遍历其他的相邻节点。而广度优先遍历则是从某个起始点开始，依次遍历该节点的所有相邻节点，然后再依次遍历这些相邻节点的相邻节点，直到遍历完图中所有节点。

以Spring Boot项目中的REST API接口为例，可以通过遍历接口中的URI路径，实现DFS和BFS算法。具体实现可以在Spring Boot的控制器类中编写遍历代码，如下所示：

java

// DFS遍历实现
@GetMapping("/dfs")
public List<String> dfs() {
    List<String> result = new ArrayList<String>();
    Stack<String> stack = new Stack<String>();
    stack.push("/");
    while (!stack.empty()) {
        String path = stack.pop();
        result.add(path);
        String[] subs = getSubPaths(path); // 获取当前路径的子路径
        for (String sub : subs) {
            stack.push(sub);
        }
    }
    return result;
}

// BFS遍历实现
@GetMapping("/bfs")
public List<String> bfs() {
    List<String> result = new ArrayList<String>();
    Queue<String> queue = new LinkedList<String>();
    queue.offer("/");
    while (!queue.isEmpty()) {
        String path = queue.poll();
        result.add(path);
        String[] subs = getSubPaths(path); // 获取当前路径的子路径
        for (String sub : subs) {
            queue.offer(sub);
        }
    }
    return result;
}

// 获取路径的子路径
private String[] getSubPaths(String path) {
    // 从Spring MVC的RequestMappingHandlerMapping中获取当前路径的所有子路径
    RequestMappingHandlerMapping handlerMapping = applicationContext.getBean(RequestMappingHandlerMapping.class);
    Map<RequestMappingInfo, HandlerMethod> map = handlerMapping.getHandlerMethods();
    Set<String> subs = new HashSet<String>();
    for (RequestMappingInfo info : map.keySet()) {
        String pattern = info.getPatternsCondition().getPatterns().iterator().next();
        if (pattern.startsWith(path) && !pattern.equals(path)) {
            int index = pattern.indexOf("/", path.length() + 1);
            if (index > -1) {
                subs.add(pattern.substring(0, index + 1));
            } else {
                subs.add(pattern);
            }
        }
    }
    return subs.toArray(new String[subs.size()]);
}

以上代码中，getSubPaths()方法使用Spring MVC的RequestMappingHandlerMapping获取所有的REST API接口路径，并过滤出当前路径的子路径。DFS遍历使用栈来实现，BFS遍历使用队列来实现。当遍历完成后，返回遍历得到的路径列表。这样，就可以使用REST API接口来演示DFS和BFS算法的实现了。文章来源地址https://www.toymoban.com/news/detail-671167.html

到了这里，关于【Spring Boot】什么是深度优先遍历与广度优先遍历？用Spring Boot项目举例说明。的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！