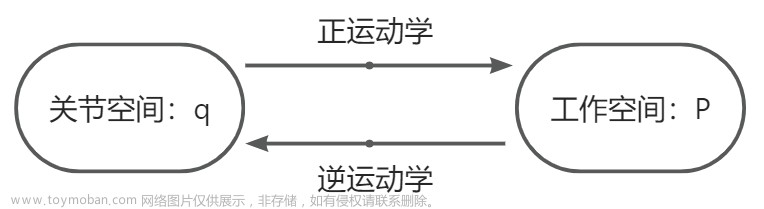
机器人学基础
二、机器人运动学
2.3 变换矩阵
(1)齐次坐标系变换
2.1,2.1中讨论了坐标系及其平移,旋转两种变换。在实际应用中两个坐标系之间的关系往往既有平移又有旋转,因此这篇文章我们将讨论一下如何以一种更为紧凑的方式来表达两个坐标系之间的位置及姿态关系。
可以把这个问题分解开来看,详细说来就是当无法一下看出两个坐标系{A}和{B}的变换关系时,可以尝试在这两个坐标系之间插入一个中间坐标系{C},只要找到了坐标系{A}和{C}的关系,然后又找到了坐标系{C}和{B}的关系,那么我们就可以间接确定{A}和{B}之间的关系。
(2)坐标系之间的位姿关系
如下图所示,坐标系{A}经过平移变换可以得到坐标系{C},坐标系{C}绕其自身z轴旋转可以得到坐标系{B}。根据我们在机器人正运动学—坐标系及其变换中提到的方法,我们可以很容易的确定坐标系{A}与{C}之间的关系可以表达为:
p
M
A
=
p
M
C
+
p
C
o
r
g
A
p_M^A=p_M^C+p_{Corg}^A
pMA=pMC+pCorgA
等式的左侧是空间中任意一点M在坐标系{A}中的坐标;等式右侧
p
M
C
p_M^C
pMC代表点M在坐标系{C}中的坐标;
p
C
o
r
g
A
p_{Corg}^A
pCorgA代表坐标系C的原点Corg(the origin of axis {C})在坐标系{A}中的坐标。
考虑完了坐标系{A}和{C}之间的平移关系,接下来我们讨论坐标系{B}和{C}之间的旋转关系,前面我们已经叙述了坐标系{B}的由来,它是坐标系{C}沿着其z轴旋转一个角度θ而来。因此,按照上一篇文章机器人正运动学—理解变换矩阵中提到的方法,将坐标系{B}的各轴单位矢量在坐标系{C}下投影即可得到坐标系{B}与坐标系{C}的姿态变换关系,如下式所示:
p M C = C R B + p M B p_M^C=^C{R_B}+p_M^B pMC=CRB+pMB
旋转矩阵:
C
R
B
^C{R^B}
CRB的各列分别是坐标系{B}三个坐标轴单位矢量在坐标系{C}三个轴上的投影。我们再来解释一下上述坐标变换等式的含义,左侧代表空间点M在坐标系{C}中的坐标;等式右侧:
C
R
B
^C{R^B}
CRB为坐标系{B}和{C}之间的变换关系;
p
M
B
p_M^B
pMB代表点M在坐标系{B}中的坐标.接下来问题来了,有了坐标系{A}和{C}的关系,也有了坐标系{B}和{C}的关系,我们如何得到坐标系{A}和{B}之间的变换呢?
第一个是从变换的角度,假设空间一点M在坐标系{B}中坐标已知,为
p
M
B
p_M^B
pMB 。那么通过坐标系{B}和{C}的变换关系,我们就可以得到点M在坐标系{C}下的坐标
p
M
C
p_M^C
pMC而我们又知道坐标系{A}和坐标系{C}之间的关系,因此我们可以最终得到点M在坐标系{A}中的坐标
p
M
A
p_M^A
pMA 。
第二个是从数学的角度,说白了就是将坐标系{B}和{C}的变换关系代入到坐标系{A}和坐标系{C}之间的关系就可以得到坐标系{A}和{B}之间的关系。这个关系可以用下式表示:
p
M
A
=
A
R
B
∗
p
M
B
+
p
B
o
r
g
A
p_M^A=^A{R_B}*p_M^B+p_{Borg}^A
pMA=ARB∗pMB+pBorgA
注意由于坐标系{B}和{C}原点是重合的,因此:
p
B
o
r
g
A
=
p
C
o
r
g
A
p_{Borg}^A=p_{Corg}^A
pBorgA=pCorgA
又因为坐标系{A}和{C}各个轴分别平行,因此:
A
R
B
=
C
R
B
^A{R_B}=^C{R_B}
ARB=CRB
(3)齐次变换矩阵
引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法,得到最终的齐次变换矩阵,这样任意两个坐标系{A}和{B}的位姿关系可以重新形式化为:
推导公式:
(4)齐次变换矩阵的三种表示
斯坦福大学公开课—机器人学,这门课对这三种解读给出了很恰当的总结:坐标系表示(coordinate representation)、坐标系变换(coordinate transformation)、点的操作算子(point operator)。接下来我们分别对它们进行解释。
坐标系表示
所谓坐标系表示指的是,齐次变换矩阵可以用来表示一个坐标系。我们来看如图两个坐标系{A}和{B}。我们知道坐标系{A}和坐标系{B}之间的关系为:
旋转矩阵
A
R
B
^A{R_B}
ARB表示{A}和{B}的姿态关系代表的是坐标系{B}三个轴的单位矢量在坐标系{A}中的投影,即在坐标系{A}中坐标系{B}的三轴单位矢量的坐标。
p
B
o
r
g
A
p_{Borg}^A
pBorgA表示{A}和{B}的位置关系,代表的是坐标系{B}的原点在坐标系{A}中的坐标。
要想唯一确定一个坐标系需要两个要素,一个是原点,一个是轴矢量。这两个要素在上面的齐次变换矩阵中已经全部包含了,因此我们说齐次变换矩阵可以用来表示一个坐标系,而
A
T
B
^A{T_B}
ATB就是坐标系{B}在坐标系{A}中的表示.
坐标系变换
所谓坐标系变换指的是,齐次变换矩阵可以用来描述一个坐标系经过怎样的平移和旋转能够变换到另一个坐标系。举个例子,两个坐标系{A}和{B}之间的齐次变换矩阵可以表示为:
其中
r
o
t
x
(
π
/
4
)
rot_x (π/4)
rotx(π/4)代表绕x轴旋转(π/4)对应的旋转矩阵,trans(1,2,3),代表在x,y,z.方向上平移1,2,3。这个时候我们就可以通过对坐标系{A}进行一些平移和旋转最终与坐标系{B}重合。这个操作过程对应于下面这张图。
把这个操作过程分为两个步骤。
第一步将坐标系{A}沿着橘色的向量平移至与坐标系{C}重合,我们很容易知道这个平移量是trans(1,2,3).
第二步将坐标系{C}绕它的x轴旋转至与坐标系{B}重合,同样容易知道这个旋转量
r
o
t
x
(
π
/
4
)
)
rot_x (π/4))
rotx(π/4))。因此我们说齐次变换矩阵可以用来描述坐标系的变换关系,而
就是坐标系{A}经过平移和旋转可以得到坐标系{B}。我们可以形象地描述(不一定恰当)这个变换为:
B
=
A
∗
A
T
B
{{B}}={A}*^A{T_B}
B=A∗ATB
点的操作算子
所谓点的操作算子指的是,齐次变换矩阵可以用来对同一个坐标系内的点进行平移和旋转操作。注意这种理解和前面两种大不一样。前两种都是在描述两个坐标系之间的关系。在讨论齐次变换矩阵对点的操作时我们的讨论仅限于一个坐标系。
举个例子在坐标系{A}中有一个点
P
0
P_0
P0,这个点绕坐标系{A}的x轴旋转π/4,得到一个新的点
P
1
P_1
P1 。写出如下的变换矩阵: 用这个变换矩阵去乘点
P
0
P_0
P0 就可以得到点
P
1
P_1
P1 。
用这个变换矩阵去乘点
P
0
P_0
P0 就可以得到点
P
1
P_1
P1 。
这个时候我们假设有一个坐标系{B}开始时与坐标系{A}完全重合,而点
P
0
P_0
P0, 又固定在坐标系{B}中,这样在把点
P
0
P_0
P0 绕坐标系{A}的轴旋转π/4时,坐标系{B}同样是绕坐标系{A}的x轴旋转π/4。此时两个坐标系之间的变换矩阵即为rotx(π/4)。由于点
P
0
P_0
P0,固定在坐标系{B}中,因此其在坐标系{B}中的坐标不变,因此经过旋转之后点
P
0
P_0
P0,在坐标系{A}中的坐标即为rotx(π/4)
P
0
P_0
P0 。可以看出这个点就是前面提到的在坐标系{A}中的
P
1
P_1
P1 点。
光用文字来描述似乎有些凌乱,下面我们用图把上面一段话再重新捋一遍,首先我们假设空间中一点
P
0
P_0
P0 在坐标系{A}中的坐标为
P
0
(
y
0
,
z
0
)
P_0 (y_0,z_0 )
P0(y0,z0),为了便于看图,坐标系我们只画出y,z两个轴,所有点的x坐标均为0。与点
P
0
P_0
P0 固连的坐标系称为{B}。坐标系{B}最开始与坐标系{A}重合,如下图所示就是问题的初始状态。
接下来开始旋转操作。我们是希望点
P
0
P_0
P0 沿坐标系{A}的x轴旋转π/4,注意因为坐标系{B}和点
P
0
P_0
P0 是固连在一起的,所以坐标系{B}也会绕着坐标系{A}的x轴旋转π/4,经过旋转之后就得到如下的图的状态:
点
P
1
P_1
P1 就是点
P
0
P_0
P0 旋转之后对应的点。这里有一点需要特别注意,由于坐标系{B}与点P_0 固连,那么经过旋转后得到的点
P
1
P_1
P1 在坐标系{B}中的坐标数值实际上没有发生任何变化(和最开始的时候点
P
0
P_0
P0 在坐标系{A}中的坐标值是一样的). 下面我们把变换前后的两种状态合并起来得到下面的图.
至此我们可以得出这样一个结论,点
P
0
P_0
P0 在坐标系{A}中的坐标值与点
P
1
P_1
P1 在{B}中的坐标值是一致的。那么如何求解点
P
1
P_1
P1在坐标系{A}中的坐标值呢?仔细思考一下是不是这样一种表达:
P
1
A
=
R
A
B
∗
P
1
B
P_1^A=R_A^B*P_1^B
P1A=RAB∗P1B
解释一下这个公式,
P
1
A
P_1^A
P1A 代表点
P
1
P_1
P1 在坐标系{A}下的坐标。
P
1
B
P_1^B
P1B 代表
P
1
P_1
P1 在坐标系{B}下的坐标。还记得我们之前说的吗,
P
1
P_1
P1 在坐标系{B}下的坐标数值上与
P
0
P_0
P0在坐标系{A}中的坐标数值一致!以上公式可以改写为:
P
1
A
=
R
A
B
∗
P
0
A
P_1^A=R_A^B*P_0^A
P1A=RAB∗P0A
至此我们看到
R
B
A
R_B^A
RBA 实现了将点
P
0
P_0
P0 旋转到
P
1
P_1
P1 点。你也可以清晰的看到上一个公式点的上标都是A,和我们之前说的同一个空间点在不同坐标系下的表达还是有区别的。
多重变换时的顺序
在此我们解决文章开头提出的多重变换时如何排列变换矩阵。其实就是两种情况,第一种情况是所有的变换都相对于最开始的坐标系;第二种情况是所有变换都相对于新得到的坐标系。我们分情况讨论。
第一种情况,坐标系{A}绕其x轴旋转α得到坐标系{B},之后坐标系{B}又绕坐标系{A}的y轴旋转β得到坐标系{C}。此时我们用对齐次变换矩阵的第三种理解来求得坐标系{C}和坐标系{A}之间的关系。我们假设在坐标系{A}中有一个点
P
0
P_0
P0,在第一次变换时我们假设有一个坐标系{T1}与坐标系{A}重合,同时点
P
0
P_0
P0 固定在坐标系{T1}中,经过第一次变换后得到在{A}中新的点
P
1
P_1
P1 的坐标为
r
o
t
x
(
α
)
P
0
rot_x (α)P_0
rotx(α)P0 (注意这是
P
1
P_1
P1 点在坐标系{A}中的坐标)。在第二次变换时我们假设又有一个坐标系{T2}与坐标系{A}重合,同时点
P
1
P_1
P1 又固定在坐标系{T2}中,经过第二次变换后得到在{A}中新的点
P
2
P_2
P2 的坐标为:
,因此我们可以最终确定坐标系{A}和{C}之间的变换关系为:
第二种情况,坐标系{A}绕其x轴旋转α得到坐标系{B},之后坐标系{B}又绕其y轴旋转β(注意这里是绕坐标系{B}的y轴)。此时我们用齐次变换矩阵的第二种理解来求坐标系{C}和坐标系{A}之间的关系。设空间中有一个点P,它在坐标系{C}中的坐标为P_C,我们首先看坐标系{B}和坐标系{C}之间的关系,由于{B}绕自身的y轴旋转β就可以得到{C},因此,同一个空间点
P在坐标系{B}中的坐标为:
。我们又知道坐标系{A}绕其x轴旋转α得到坐标系{B},因此,同一个空间点P在坐标系{A}中的坐标为
,因此我们可以最终确定坐标系{A}和{C}之间的变换关系为:
这也验证了文章开头提出的结论,那就是绕着原坐标系旋转就倒着乘,绕着新坐标系旋转就正着乘。
(5)齐次变换矩阵的逆
齐次变换矩阵的逆表达式为:
当你充分理解了齐次变换矩阵的本质后,它的逆是可以直接写出来的,无需特别记忆。通常而言求任意矩阵的逆是比较困难的。但是由于齐次变换矩阵的良好性质以及很强的几何特征,我们很容易直接写出它的逆。已知如下的齐次变换矩阵:
首先看旋转部分,在文章机器人正运动学—理解变换矩阵中我们提到过
A
R
B
^AR_B
ARB的列代表坐标系{B}的三轴矢量在坐标系{A}中的投影,行代表坐标系{A}的三轴矢量在坐标系{B}中的投影,因此,
A
R
B
^AR_B
ARB的转置就是其逆。
其次来看平移部分,
p
B
r
o
g
A
p_{Brog}^A
pBrogA代表坐标系{B}的原点在坐标系{A}中的坐标,而我们需要的是坐标系{A}的原点在坐标系{B}中的坐标,即
p
A
r
o
g
B
p_{Arog}^B
pArogB,从几何的角度看,这两个向量恰好是相反向量,因此我们首先把向量
p
B
r
o
g
A
p_{Brog}^A
pBrogA取反得到
−
p
A
r
o
g
B
-p_{Arog}^B
−pArogB。到这一步还没有完,因为目前为止这个向量是在坐标系{A}中描述的,因此我们要将它变换到坐标系{B}中的描述,即为
−
A
R
B
T
∗
p
B
r
o
g
A
-^AR_B^T*p_{Brog}^A
−ARBT∗pBrogA,其中
−
A
R
B
T
-^AR_B^T
−ARBT代表
A
R
B
^AR_B
ARB的转置。 至此我们得到了坐标系{A}相对于坐标系{B}的姿态
A
R
B
^AR_B
ARB,以及坐标系{B}中描述的坐标系{A}原点坐标: 文章来源:https://www.toymoban.com/news/detail-671310.html
文章来源:https://www.toymoban.com/news/detail-671310.html
。因此变换矩阵的逆即为:
参考: https://www.guyuehome.com/19819文章来源地址https://www.toymoban.com/news/detail-671310.html
到了这里,关于机器人学基础--运动学--2.3 变换矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!