C# 使用递归方法实现汉诺塔步数计算-Toy模板网

这篇具有很好参考价值的文章主要介绍了C# 使用递归方法实现汉诺塔步数计算。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

Part 1 什么是递归

举一个例子：计算从 1 到 x 的总和

public int SumFrom1ToX(int x)
{
    if(x == 1)
    {
        return 1;
    }
    else
    {
        int result = x + SumFrom1ToX_2(x - 1);  // 调用自己
        return result;
    }
}

Part 2 汉诺塔

有三个石柱，在最左侧的石柱上从小到大摆放 N 层盘片，需要从最左侧的石柱移动到最右侧的石柱上，中间的石柱作为缓冲，一次只能移动一个盘片，且无论何时较小的盘片始终在较大的盘片上面。
这个问题求解这过程中搬运的次数

Part 3 程序

创建一个Move函数来移动盘子

static void Move(int pile, char src, char temp, char dst)
{

}

pile 是最左侧的盘片数量，src 是起始点，temp 是中间的缓冲区，dst 是终点

Move(pile - 1, src, dst, temp); // 将pile-1层盘片从src经过dst移动到temp
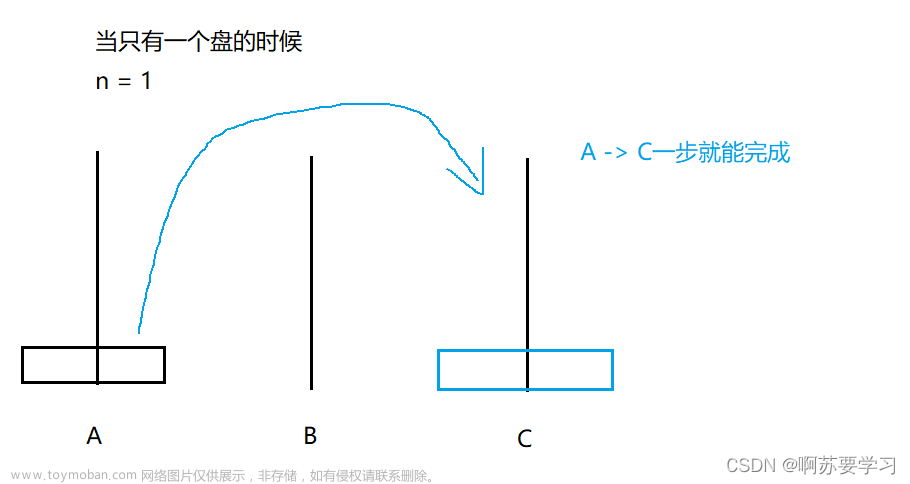
Move(1, src, temp, dst); // 将最底层的盘片从src移动到dst
Move(pile - 1, tmp, src, dst); // 将pile-1层汉诺塔从temp经过src移动到dst

Move 方法的代码

static void Move(int pile, char src, char temp, char dst)
{
    if (pile == 1)
    {
        Console.WriteLine($"{src} --> {dst}");
        steps++;
        return;
    }

    Move(pile - 1, src, dst, temp);
    Move(1, src, temp, dst);
    Move(pile - 1, temp, src, dst);
}

完整代码

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Linq;
using System.Reflection;
using System.Text;
using System.Threading.Tasks;

namespace ConsoleHelloWorld
{
    class Hanoi
    {
        public static int steps = 0;

        public void ShowHanoiPath(int levels)
        {
            Console.WriteLine("输入的汉诺塔层数是：{0}", levels);
            Move(levels, 'A', 'B', 'C');
            Console.WriteLine("一共移动了{0}次", steps);
        }

        static void Move(int pile, char src, char temp, char dst)
        {
            if (pile == 1)
            {
                Console.WriteLine($"{src} --> {dst}");
                steps++;
                return;
            }

            Move(pile - 1, src, dst, temp);
            Move(1, src, temp, dst);
            Move(pile - 1, temp, src, dst);
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            Hanoi hanoi = new Hanoi();
            hanoi.ShowHanoiPath(4);
        }
    }
}