线性代数(五) 线性空间

前言

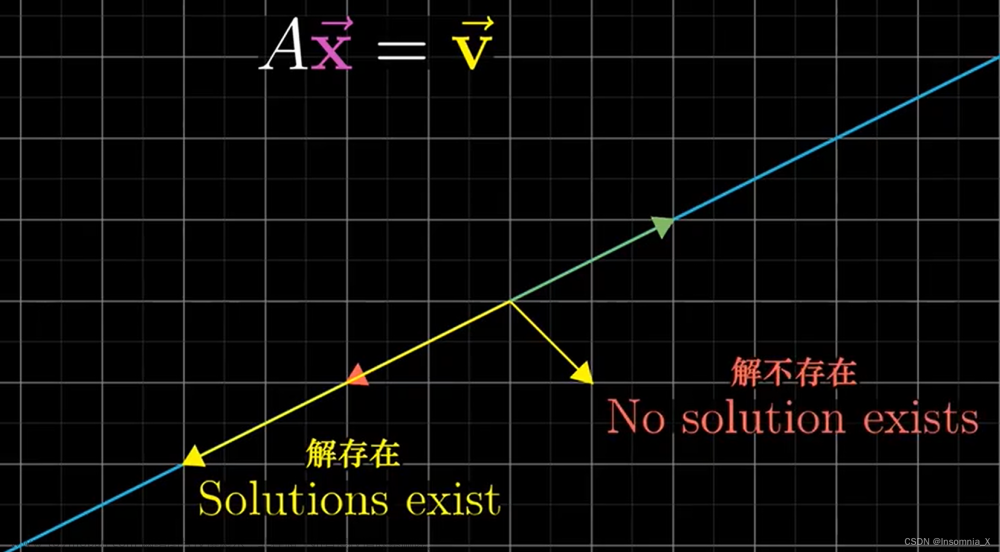
《线性代数(三) 线性方程组&向量空间》我通过解线性方程组的方式去理解线性空间。此章从另一个角度去理解

空间是什么

大家较熟悉的：平面直角坐标系是最常见的二维空间

空间由无穷多个坐标点组成

每个坐标点就是一个向量

• 反过来，也可说：2维空间，是由无穷多个2维向量构成
• 同样的，在3维空间中，每个3维坐标点就是一个3维向量
• 那么同理：3维空间中有无穷多个3维向量，或3维空间由无穷多个3维向量构成

空间中所有向量，都可被表示成 $e_1,e_2,...,e_n$的线性组合,若有一向量记为:$a$
$$a=k_1\cdot e_1+k_2\cdot e_2+...+k_n\cdot e_n，k_1,k_2,...,k_n有解即可$$
则称：这些向量$e_1,e_2,...,e_n$为这个空间基

线性空间定义及性质

向量相加

$$\left[\begin{array}{c}{x}_1\\ y_1\end{array}\right]+\left[\begin{array}{c}{x}_2\\ y_2\end{array}\right]=\left[\begin{array}{c}{x}_1+x_2\\ y_1+y_2\end{array}\right]=\left[\begin{array}{c}2+3\\ 4+1\end{array}\right]$$

数与向量乘法

$$\left[\begin{array}{c}x\\ y\end{array}\right]\ast 2=\left[\begin{array}{c}2x\\ 2y\end{array}\right]$$

维数,坐标和基

这里出现了一个线性无关的概念，这里线性无关的概念和向量空间中的线性无关差不多，但向量的范围变广了。

1. n维线性空间V的基不是唯一的。V中的任意n个线性无关向量都是V的一组基
2. 向量$a$的坐标$(a_1,a_2,...a_n)$在$({\epsilon }_1,{\epsilon }_2,...{\epsilon }_n)$基下，是唯一且确定的

要怎么确定线性空间的维数与基

欧几里得空间

欧几里得空间是空间中的一种类型，是一种特殊的集合。欧几里得集合中的元素：有序实数元组

例：(2,3)(2,4)(3,4)(3,5)为有序实数2元组

• 有序是指：如(2,3)和(3,2)是两个不同的元素
• 也就是：每个元素内的实数是讲顺序的
• 实数是指：每个元素内的数字都∈R
• 元组是指：每个元素有有序几个数字构成
• 如：2个数字构成=2元组，n个数字构成=n元组

欧几里得集合=有序实数元组=n维坐标点的集合
所以，欧几里得空间就是我们从小到大进场使用的那个空间

欧几里得空间符合空间的8大定理

子空间

子空间，是整个空间的一部分。但它也是空间，必须满足向量空间的定义。

子空间的交集

子空间的和

子空间的$V_1,V_2$的并集，并不是简单的元素相加，造成“子空间的并集不属于子空间”。

所以定义子空间的和

子空间的直和

子空间直和是特殊的和。基要求各子空间互相独立。

可以把整个线性空间看成一个大蛋糕。

• 直和分解就是把蛋糕切成小块的，每一小块蛋糕都是一个子空间，所有小蛋糕之间没有交集，且它们能拼成整个蛋糕。
• 子空间的和就是分蛋糕的时候没切好，小蛋糕拼不成整个蛋糕(子空间之间的交集非空).

商空间

这里的等价类$\bar{a}=a+W$,称$\bar{a}$是$W$的一个陪集，$a$是陪集代表。

其具有性质如下

1. 加法运算:$\alpha +W+\beta +W=(\alpha +\beta )+W$
2. 纯量乘法运算:$k(\alpha +W)=k\alpha +W$
3. $dim(V/W)=dimV-dimW$
4. 

内积空间

在之前的内容中，我们抽象的介绍了向量，矩阵以及线性空间线性变换等。但是在几何中，向量还有向量的模，向量的内积运算等。为了引入向量的模，向量的内积等运算，我们引入了“内积定义”。即内积空间=线性空间+内积定义。

向量的夹角

$$\cos \theta =\cos (\alpha -\beta )=\cos (\alpha )\cos (\beta )+\sin (\alpha )\sin (\beta )=\frac{x_1}{\sqrt{x_1^2+y_1^2}}\ast \frac{x_2}{\sqrt{x_2^2+y_2^2}}+\frac{y_1}{\sqrt{x_1^2+y_1^2}}\ast \frac{y_2}{\sqrt{x_2^2+y_2^2}}$$
$$\cos \theta =\frac{x_1{x}_2+y_1{y}_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}=\frac{a\ast b}{|a||b|}$$

上述的a,b向量，只是在2维坐标系中，如果将坐标系转为n维度,即向量a为(x1,x2,x3…xn)向量b为(y1,y2,y3…yn)
$$\cos \theta =\frac{{\sum }_{i=1}^n(x_i\ast y_i)}{\sqrt{{\sum }_{i=1}^n{x}_i^2}\sqrt{{\sum }_{i=1}^n{y}_i^2}}=\frac{[a,b]}{\sqrt{[a,a]}\sqrt{[b,b]}}$$

两个向量的夹角$\theta$=90°，即两个向量正交.

两个向量相互正交，把这2个向量合为一组向量，就叫正交向量组

正交基

如果$|e_n|=1$,则称为标准正交基

施密特（Schmidt）求解正交基

通过简单的投影方式，可以找到一基的正交基

已知一组基{${\alpha }_1,{\alpha }_2$}求其正交基组

1. 令${\beta }_1={\alpha }_1$
2. 得${\beta }_1$的上的单位基为$\frac{{\beta }_1}{\sqrt{[{\beta }_1,{\beta }_1]}}$
3. 计算${\alpha }_1$在${\beta }_1$上的投影
4. 计算投影长度，$\frac{[{\alpha }_2,{\beta }_1]}{\sqrt{[{\alpha }_2,{\alpha }_2]}\sqrt{[{\beta }_1,{\beta }_1]}}\ast \sqrt{[{\alpha }_2,{\alpha }_2]}$
5. 投影为长度*${\beta }_1$的上的单位基$\frac{[{\alpha }_2,{\beta }_1]}{[{\beta }_1,{\beta }_1]}\ast {\beta }_1$
6. 得正交基为${\alpha }_2-\frac{[{\alpha }_2,{\beta }_1]}{[{\beta }_1,{\beta }_1]}\ast {\beta }_1$
7. 正交基组为{${\alpha }_2-\frac{[{\alpha }_2,{\beta }_1]}{[{\beta }_1,{\beta }_1]}\ast {\beta }_1,\frac{[{\alpha }_2,{\beta }_1]}{[{\beta }_1,{\beta }_1]}\ast {\beta }_1$}

如果是三维的话

正交补

定义： 设$U$是$V$的子空间，则 U ⊥ = { v ∈ V : ∀ u ∈ U < v , u > = 0 } U^\perp =\{v\in V : \forall u\in U \left< v,u\right> =0 \} U⊥={v∈V:∀u∈U⟨v,u⟩=0}称之为$U$的正交补.$\forall u$表示集合中所有u的意思

1. $U^{\perp }$是$V$的子空间;
2. V ⊥ = { 0 } V^\perp=\{0\} V⊥={0}且 { 0 } ⊥ = V \{0\}^\perp=V {0}⊥=V
3. U ⊥ ∩ U = { 0 } U^\perp \cap U = \{0\} U⊥∩U={0};
4. 如果 $U,W$都是 $V$的子集，且 $U\subseteq W$ ，则 $W^{\perp }\subseteq U^{\perp }$

定理： 有限维子空间的正交分解： $V=U\oplus U^{\perp }$

1. $(U^{\perp }{)}^{\perp }=U$
2. $\dim V=\dim U+\dim U^{\perp }$

如何求解正交补的基？

1. 假设 d i m V = 3 , d i m U = 2 且基组为 [ { 1 , 0 , 0 } , { 0 , 1 , 0 } ] dim V = 3 , dim U = 2 且基组为[\{1,0,0\},\{0,1,0\}] dimV=3,dimU=2且基组为[{1,0,0},{0,1,0}]
2. 得矩阵 A = [ 1 0 0 0 1 0 0 0 0 ] A=\begin{bmatrix} 1 &0&0 \\ 0&1&0 \\ 0&0&0 \end{bmatrix} A= ​100​010​000​ ​
3. 假设$U^{\perp }$的基组 x ⃗ = [ x y z ] \vec{x}=\begin{bmatrix} x\\ y\\ z \end{bmatrix} x = ​xyz​ ​
4. 得$Ax=0$齐次方程组，你通解为{0,0,1}

正交补的基就是方程组的解，解数=dim V - R(A)

主要参考

《欧几里得空间是向量空间》
《生成空间是什么》
《子空间的交与和》
《3.10子空间的运算》
《正交基与标准正交基》
《如何理解施密特（Schmidt）正交化》
《正交补 (orthogonal complements)》
《【高等代数(丘维声著）笔记】3.14商空间》文章来源地址https://www.toymoban.com/news/detail-672358.html

到了这里，关于线性代数(五) 线性空间的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！