Matlab | Lab4——用LU 分解法、 Jacobi 迭代、 Gauss-Seidel 迭代解线性病态方程组（系数矩阵为Hilbert矩阵）-Toy模板网

这篇具有很好参考价值的文章主要介绍了Matlab | Lab4——用LU 分解法、 Jacobi 迭代、 Gauss-Seidel 迭代解线性病态方程组（系数矩阵为Hilbert矩阵）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.要求

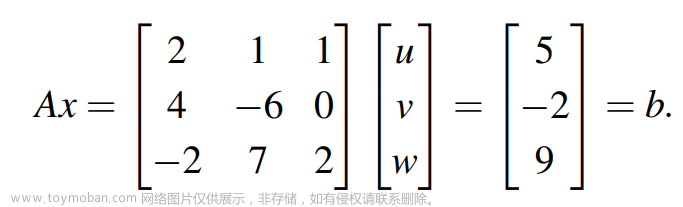
考虑线性方程组Hx=b，其中H为n阶Hilbert矩阵，即 $病态方程组求解方法机器学习,计算方法lab,matlab,线性代数,矩阵$

通过先给定解（例如取x的各个分量为1）,再计算出右端向量b的办法给出一个精确解已知的问题．

(1)分别编写Doolittle LU 分解法、 Jacobi 迭代、 Gauss-Seidel 迭代的一般程序；

(2)取阶数n=6，分别用 LU 分解法、 Jacobi 迭代、 Gauss-Seidel 迭代去求解上述的病态方程组Hx = b；分别报告它们的数值结果(包括数值解、迭代步数)以及它们在1-范数下的计算误差。迭代法的停止条件均取为 $病态方程组求解方法机器学习,计算方法lab,matlab,线性代数,矩阵$

2.Matlab实现（取迭代初值为0）

2.1.1 LU分解函数

function [L,U,y,x] = LU(A, b) 
% LU矩阵分解
% inputs:
%        A:输入的系数矩阵，大小为[n,n]
%        B:输入的乘积向量，大小为n
% outputs:
%        L:下三角阵，大小为[n,n]
%        U:上三角阵，大小为[n,n]
%        y:中间矩阵，大小为n
%        x:结果矩阵，大小为n

%% 第一步：初始化
% 获取n值
[arow, acol] = size(A);

%% 计算L,U矩阵
for i=1:arow
    L(i,i)=1; %L对角线是1
end
for j=1:acol  %U第一行
    U(1,j)=A(1,j);
end
for k=2:arow  %L第一列
    L(k,1)=A(k,1)/U(1,1);
end
for m=2:(arow-1)
    for j=m:arow %m右下角缺少
        s1=0;
        for k=1:(m-1)
            s1=s1+L(m,k)*U(k,j);
        end
        U(m,j)=A(m,j)-s1;
    end
    for i=(m+1):arow
        s2=0;
        for k=1:m-1
            s2=s2+L(i,k)*U(k,m);
        end
        L(i,m)=(A(i,m)-s2)/U(m,m);
    end
end
s1=0;
for k=1:(arow-1)
    s1=s1+L(arow,k)*U(k,acol);
end
U(arow,acol)=A(arow,acol)-s1; %补上U的右下

%% 计算y
n=arow;
y(1)=b(1);
for i=2:n 
    s=0;
    for k=1:(i-1)
        s=s+L(i,k)*y(k);
    end
    y(i)=b(i)-s;
end

%% 计算x
x(n)=y(n)/U(n,n);

for i=1:(n-1)
    s=0;
    for k=0:(i-1)
        s=s+U(n-i,n-k)*x(n-k);
    end
    x(n-i)=(y(n-i)-s)/U(n-i,n-i);
end
end

2.1.2 LU分解

%% n=6
for i=1:6
    for j=1:6
        a(i,j)=1/(i+j-1);
    end
end


for i=1:6
    s=0;
    for j=1:6
        s=s+a(i,j);
    end
    b(i)=s;
end


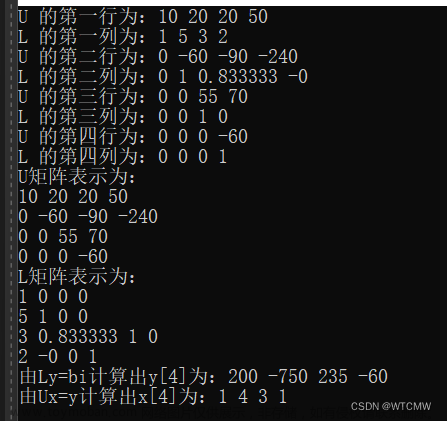
[L1,U1,Y1,X1] = LU(a,b);
X1
Y1
L1
U1

2.2.1 Jacobi迭代函数

function [x2] = Jacobi(x1,a,b)
%输入要迭代的一组x记作x1,输出迭代后的x记作x2
n=length(x1);
s=0;
for k=2:n
    s=s+a(1,k)*x1(k);
end
x2(1)=(b(1)-s)/a(1,1);
for i=2:(n-1)
    s1=0;
    s2=0;
    for j=1:(i-1)
        s1=s1+a(i,j)*x1(j);
    end
    for j=(i+1):n
        s1=s1+a(i,j)*x1(j);
    end
    x2(i)=(b(i)-s1-s2)/a(i,i);
end
s=0;
for j=1:(n-1)
    s=s+a(n,j)*x1(j);
end
x2(n)=(b(n)-s)/a(n,n);
end

2.2.2 Jacobi迭代（结果为inf）

%% n=6
for i=1:6
    for j=1:6
        a(i,j)=1/(i+j-1);
    end
end
b=[];
for i=1:6
    s=0;
    for j=1:6
        s=s+a(i,j);
    end
    b(i)=s;
end
x1=[0,0,0,0,0,0];
x0=[1,1,1,1,1,1];
for p=0:1000000
    [x2]=Jacobi(x1,a,b);
    p=p+1;
    if norm(x2-x1,1)<0.00001
        break
    end
    x1=x2;

end
x1
p
error=norm(x1-x0,1)

2.3.1 GS迭代函数

function [x] = Guass(x,a,b)
%输入要迭代的一组x记作x1,输出迭代后的x记作x2
n=length(x);
s=0;
for k=2:n
    s=s+a(1,k)*x(k);
end
x(1)=(b(1)-s)/a(1,1);
for i=2:(n-1)
    s1=0;
    s2=0;
    for j=1:(i-1)
        s1=s1+a(i,j)*x(j);
    end
    for j=(i+1):n
        s1=s1+a(i,j)*x(j);
    end
    x(i)=(b(i)-s1-s2)/a(i,i);
end
s=0;
for j=1:(n-1)
    s=s+a(n,j)*x(j);
end
x(n)=(b(n)-s)/a(n,n);
end

2.3.2 GS迭代文章来源地址https://www.toymoban.com/news/detail-672576.html

%% n=6
for i=1:6
    for j=1:6
        a(i,j)=1/(i+j-1);
    end
end
b=[];
for i=1:6
    s=0;
    for j=1:6
        s=s+a(i,j);
    end
    b(i)=s;
end
x31=[0,0,0,0,0,0];
x0=[1,1,1,1,1,1];
for p=0:100000
    [x32]=Guass(x31,a,b);
     p=p+1;
    if norm(x32-x31,1)<0.00001
        break
    end
    x31=x32;
 
end
x31
p
error=norm(x31-x0,1)

到了这里，关于Matlab | Lab4——用LU 分解法、 Jacobi 迭代、 Gauss-Seidel 迭代解线性病态方程组（系数矩阵为Hilbert矩阵）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！