lintcode 344 · 歌曲时间【背包问题，动态规划】-Toy模板网

这篇具有很好参考价值的文章主要介绍了lintcode 344 · 歌曲时间【背包问题，动态规划】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

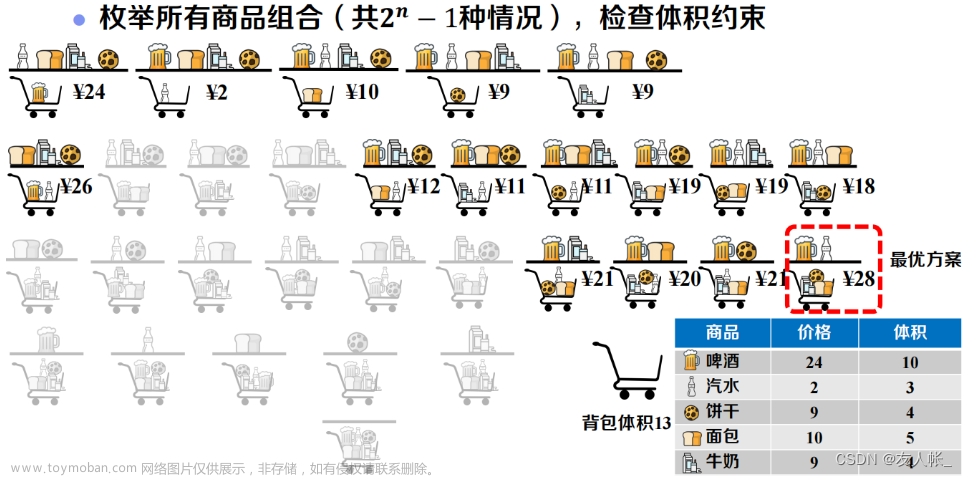
题目链接，描述

https://www.lintcode.com/problem/344/

给定长度为N的正整数数组song代表N首歌的时间
请你任选其中若干首播放，在满足开始播放最后一首歌的时间小于M的情况下求播放歌曲的最长时间
每首歌只能被播放一次
你可以任意指定播放顺序


1 \leq N \leq 10^31≤N≤10 
3
 
1 \leq M \leq 10^51≤M≤10 
5
 
1 \leq song_i \leq 10^51≤song 
i

 ≤10 
5
 

样例
输入:[1,2,3,4,5]
14
输出:15
解释:依次播放第一首歌到第五首歌

思路

我们先证明，时长最长的那首歌是一定会被选中的。如果不然，则可以将最后播放的那首歌替换成这个时长最长的，能得到更优解，矛盾。那么我们只考虑剩下的歌的选择。问题转化为，问总长度小于M MM的情况下，最长总时长是多少。这是个0 − 1 0-10−1背包问题，可以用动态规划解决文章来源地址https://www.toymoban.com/news/detail-674855.html

代码

public class Solution {
    /**
     * @param song: an array represent song'time
     * @param m: an integer represent sont time limit
     * @return: return the longest time for song
     */
    public int longestSongTime(int[] song, int m) {
            /*
         思路：1：和第92题背包问题一样的，本题只需要把最大的一个数字去掉，
        2：然后求剩余的数字背包不大于m的情况下最大是多少
        然后用这个最大值+ 第一步去掉的最大值
         */
        //return f1(song,m); //递归+缓存，超过内存限制了，代码正确的，但是不能作为答案
        
        //下面是动态规划的答案，提交他就能通过
        int n = song.length;
        int max=Integer.MIN_VALUE, maxIdx = -1;
        for (int i = 0; i < n; i++) {
            if(song[i] > max){
                max = song[i];
                maxIdx = i;
            }
        }

        song[maxIdx] =0; //最大值不参与动态规划计算，但是用于最后的结果
        int[][] dp = new int[song.length+1][m+1];
        for (int i = song.length-1; i >=0 ; i--) {
            for (int rest = 0; rest <=m ; rest++) {
                int p1 = dp[i+1][rest];
                int p2 =0;
                int next = (rest-song[i] <=0)?-1:(dp[i+1][rest-song[i]]);
                if(next!=-1){
                    p2 = next+song[i];
                }

                dp[i][rest]=Math.max(p1,p2);
            }
        }

        return dp[0][m]+max;
    }


    public static int f1(int[] song, int m) {
        //递归+缓存
        //思路：1：和第92题背包问题一样的，本题只需要把最大的一个数字去掉，
        // 2：然后求剩余的数字背包不大于m的情况下最大是多少
        //然后用这个最大值+ 第一步去掉的最大值
        int max = Integer.MIN_VALUE, maxIdx = -1;
        for (int i = 0; i < song.length; i++) {
            if (song[i] > max) {
                max = song[i];
                maxIdx = i;
            }
        }
        int n = song.length;
        song[maxIdx] = 0;
        Integer[][] dp = new Integer[n + 1][m + 1];
        int curMax = dfs(0, m, song, dp);
        return curMax + max;
    }

    public static int dfs(int i, int rest, int[] arr, Integer[][] dp) {
        if (rest <= 0) return -1;
        if (i == arr.length) return 0;

        if (dp[i][rest] != null) return dp[i][rest];
        int p1 = dfs(i + 1, rest, arr, dp);

        int p2 = 0;
        int next = dfs(i + 1, rest - arr[i], arr, dp);

        if (next != -1) {
            p2 = next + arr[i];
        }

        dp[i][rest] = Math.max(p1, p2);
        return Math.max(p1, p2);
    }
}