目录
树概念及结构
树的相关概念
树的表示
二叉树的概念及结构
堆
堆的实现
结构体建立
初始化
添加元素
打印堆
删除堆首元素
返回首元素
判断是否为空
空间销毁
刷题找工作的好网站——牛客网
牛客网 - 找工作神器|笔试题库|面试经验|实习招聘内推,求职就业一站解决_牛客网
树概念及结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
树的相关概念
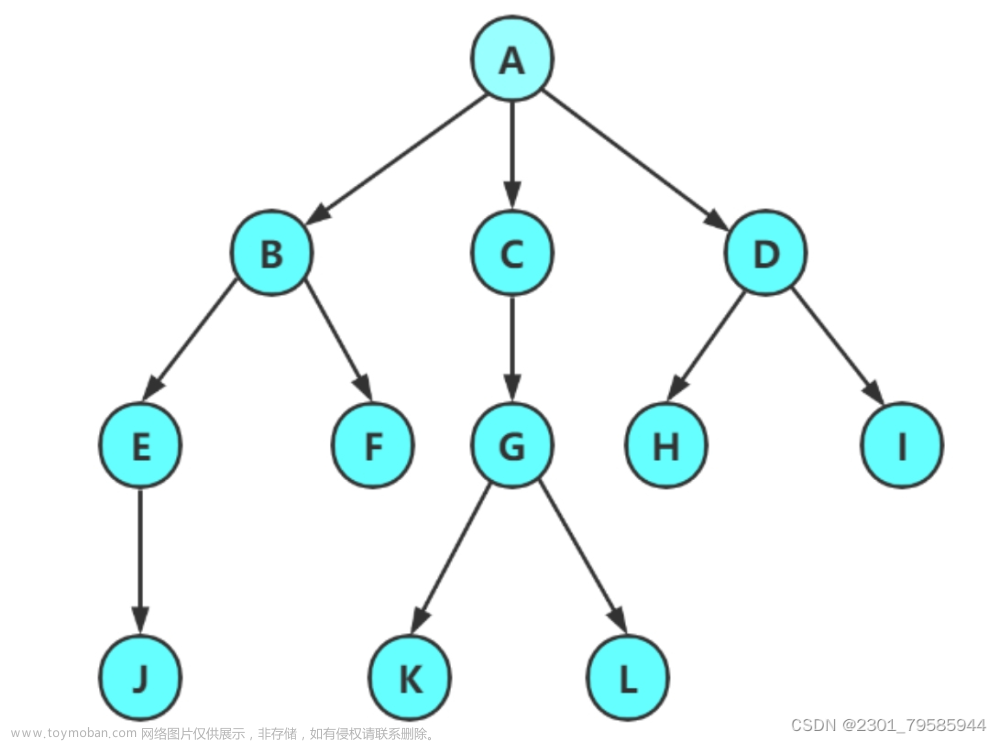
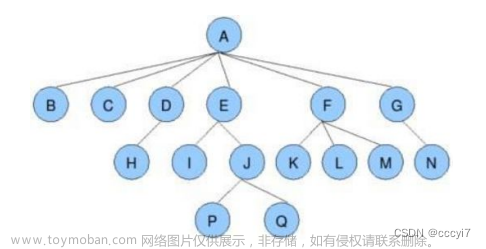
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
树的表示
1.指针数组表示
数组内存的时子节点的地址
2.二级指针表示
3.最常用的表示方法——孩子兄弟表示法
typedef int DataType; struct Node { struct Node* _firstChild1; // 第一个孩子结点 struct Node* _pNextBrother; // 指向其下一个兄弟结点 DataType _data; // 结点中的数据域 };
树在实际中的应用
二叉树的概念及结构
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树二叉树每层的节点数是2^(k-1),满二叉树节点总个数2^k-1,完全二叉树节点个数范围:[2^k-1,2^k-1],完全二叉树最后一层的个数由1到满
注意:对于任意的二叉树都是由以下几种情况复合而成的:
特殊的二叉树:
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
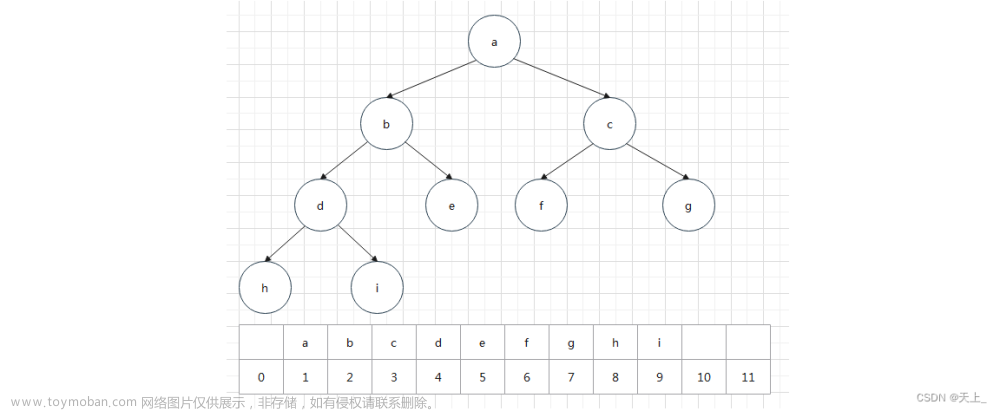
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树
堆
动态开辟的空间在堆上,这个堆是进程地址空间内存区域划分
堆(heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
堆中某个结点的值总是不大于或不小于其父结点的值;
堆总是一棵完全二叉树。
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
不管奇数偶数parent都可以这样计算
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元
堆的实现
结构体建立
typedef int HPDataTypedef;
typedef struct Heap
{
HPDataTypedef* a;
int size;//最后元素的下一个位置
int capacity;//统计容量
}HP;初始化
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->capacity = php->size = 0;
}添加元素
void Swap(HPDataTypedef* a, HPDataTypedef* b)
{
HPDataTypedef tmp = *a;
*a = *b;
*b = tmp;
}
//根据大根堆或小根堆进行调整,这里以小根堆为例
void AdjusuUp(HPDataTypedef* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0) //如果子节点=0,此时已经调整完成了,因此条件是>0
{
if (a[child]< a[parent])
{
Swap(&a[child], &a[parent]); //如果父节点<子节点,进行交换
child = parent; //更新子节点位置
parent = (child - 1) / 2; //更新父节点位置
}
else
break;
}
}
void HeapPush(HP* php, HPDataTypedef x)
{
assert(php);
if (php->capacity == php->size)
{
int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
HPDataTypedef* tmp = (HPDataTypedef*)realloc(php->a,sizeof(HPDataTypedef) * newcapacity);
if (tmp == NULL)
{
perror("malloc fail:");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size] = x;
php->size++;
AdjusuUp(php->a, php->size - 1);
}

打印堆
void HeapPrint(HP* php)
{
assert(php);
int i = 0;
for (i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
}删除堆首元素
文章来源:https://www.toymoban.com/news/detail-675404.html
向下调整的前提:左子树和右子树必须同时是大堆或小堆 文章来源地址https://www.toymoban.com/news/detail-675404.html
void AdjusuDown(HPDataTypedef* a,int n, HPDataTypedef parent)
{
HPDataTypedef minChild = parent * 2 + 1;
while (minChild<n)
{
if (minChild+1<n&&a[minChild+1] < a[minChild])
{
minChild++;
}
if (a[minChild] > a[parent])
{
Swap(&a[parent], &a[minChild]);
parent = minChild;
minChild = parent * 2 + 1;
}
else
break;
}
}
void HeapPop(HP* php)
{
Swap(&php->a[0], &php->a[php->size-1]);
php->size--;
//删除之后要让堆保持大根堆或小根堆存储的形式,这里以小根堆为例
AdjusuDown(php->a,php->size, 0);
}返回首元素
HPDataTypedef Pop(HP* php)
{
assert(php);
assert(!HeapEmpt(php));
return php->a[0];
}判断是否为空
bool HeapEmpt(HP* php)
{
assert(php);
return php->size == 0;
} //如果size==0就是空空间销毁
void Destory(HP* php)
{
free(php->a); //释放掉开辟的空间
php->capacity = php->size = 0; //让容量和个数都为0
php->a = NULL;
} 到了这里,关于数据结构——二叉树(堆的实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!