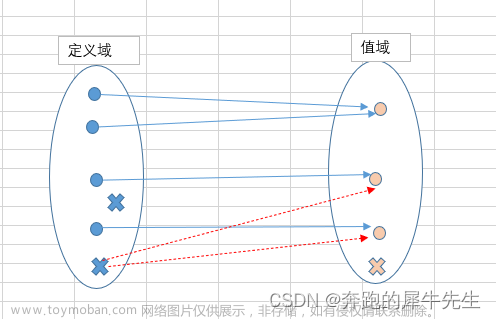
5 空间的同构
下面再谈谈同构。线性空间千千万,应如何研究呢?同构就是这样一个强大的概念,任何维数相同的线性空间之间是同构的,空间的维数是简单而深刻的,简单的自然数居然能够刻画空间最本质的性质。借助于同构,要研究任意一个n维线性空间,只要研究Rⁿ就行了。
n维线性空间作为一个整体,我们自然想到能不能先研究它的局部性质?所以自然而然的导出了子空间的概念以及整个空间的直和分解。直和分解要求把整个空间分解为两两不交的子空间之和,通过研究各个简单的子空间的性质,从而得出整个空间的性质。
文章来源地址https://www.toymoban.com/news/detail-676623.html
6 求最简矩阵
然而一个线性映射的矩阵在标准正交基下可能特别复杂,所以需要选择一组特殊的基,让它的矩阵在这个基下有最简单的矩阵表示。如果存在这样的基,使得线性映射的矩阵为对角矩阵,则称这个线性映射可对角化。
然而是不是所有线性映射都可以对角化呢,遗憾的是,并不是。那么就要问,如果一个线性映射不能对角化,那么它的最简矩阵是什么?这个问题的答案是若尔当标准型。可以证明,在复数域上,任何线性映射都存在唯一的若尔当标准型。

1 线性代数的内在逻辑脉络
1.1 逻辑脉络1 (主线?)
向量的维度
向量组的秩,和维度相关。
向量组的秩是向量组的最大线性无关组
1.2 逻辑脉络2(主线?)
比如,如果有一种矩阵,线性变换后,仍然共线,那么这种矩阵就可以求特征值和特征向量
那怎么求呢,就是用定义求
然后这些矩阵可以求矩阵的N次方 A^n ,但是n比较大了计算就比较复杂
然后就想到,如果把A转成对角矩阵就会比较简单λ
λ其实就是[λ,0;0,λ] , 那么A=λ*P,这样就把A转化为对角矩阵了
这样由矩阵A的特征值构成的矩阵,这样求A^n就快了
但是还有一个问题
AP=PA
A=PλP-
但是P-不好求
但是如果P是一个正交矩阵,就Pt=P-就很好求了
A=PλPt
因此我们要学会怎么让矩阵正交化,施密特正交化方法等等
2 线性代数的知识和其他知识的对应(换一个角度看世界)
向量,矩阵的线性代数知识和其他知识的对应
向量和矩阵的几何表示
行列式,面积的变化比
向量的长度模
向量的正交,就是垂直,但这里定义为内积=0,其实是另外一种垂直的定义方法
向量的加减乘除
加法,减法,就是向量线段的三角形法则
乘法的点乘、、
乘法的叉乘
向量的点乘
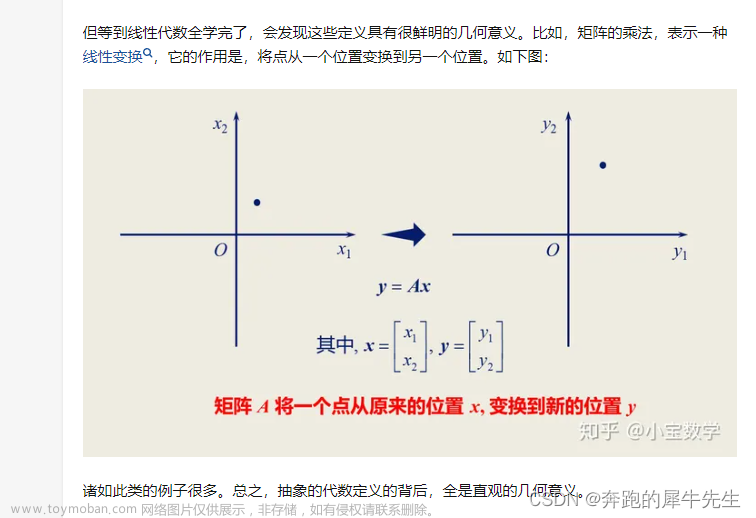
向量的叉乘,

向量的叉乘直接就是面积公式
角度公式
好像也可以用向量的方法来求
3 数学/线性代数里,其实很多东西的求得都有多种解决办法
很多概念,界定狠清晰,但是不好求
多种方法,拓宽思维
方法1:按定义直接去求解
方法2:按
2 比如求逆矩阵
概念方法,线性变化
增广矩阵
其他方法
分块矩阵
伴随矩阵
|A|=0
3 求矩阵的秩
4 求方程组的解的好方法
直接可以用行列式的方法求解啊
1.2 有没有其他方法呢?有:比如2阶行列式方法
因为二阶行列式的公式求值如下
所以二元方程组的求解也可以用行列式写成
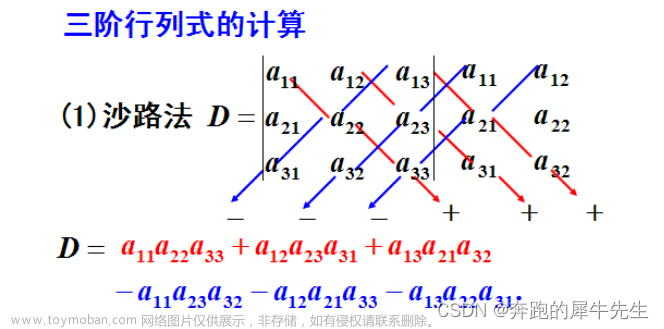
1.3 3阶行列式

- 如果 |A|≠0 ,则,矩阵A满秩,矩阵A可逆
3.3 行列式的意义和作用呢?
- 作用1:快速解出,多元方程组的解
- 作用2:通过矩阵的余子式的转置等计算,矩阵的逆矩阵
3.4 行列式的结果(是1个标量)的作用
行列数的值代表 有向面积的变化率/变化倍数
行列式的值(结构)的作用
|A| =|AT| 矩阵和对应转置矩阵的行列式相等
如果 |A|≠0 ,则,矩阵A满秩,矩阵A可逆
如果 |A|=0 ,那么就是说至少有两个向量在变换之后,共线了。参考[1,1;1,1] 矩阵的效果
如果 |A|>0 ,正值表示方向相同
如果 |A|<0 ,负值代表着翻面了,方向相反,相对位置发生了调换
————————————————
版权声明:本文为CSDN博主「奔跑的犀牛先生」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/xuemanqianshan/article/details/132390299
定理
有解的判断
- 对于线性方程组 Ax=b,如果系数矩阵A和秩 = 增广矩阵B(B=A|b)的秩,也就是rank(A) =rank(B)那么就有解
- Ax=y
- 矩阵Am*n, 而Xn*1=[x1,x2....xn] ,bm*1=[b1,b2....bm]
- rank(x) =n 单个一维向量,不存在线性相关问题,所以 n 代表定义域X的秩
- rank(b)=m 单个一维向量,不存在线性相关问题
- 因此,A的零空间 rank(A)<=min(m,n) ,rank(A) 代表值域的秩,因为值域 rank(b)=m其实被rank(A) 所决定。但是值域的秩,为啥不直接用 rank(b) 呢?
- 而 rank(null(A)) 实际就是 rank(Ax=0),所以 rank(null(A))<=min(m,n)
解的个数的判断
- 对于线性方程组 Ax=b,如果系数矩阵A和秩 = 增广矩阵B(B=A|b)的秩,并且
- 如果A是m*n的矩阵,其中n是X的秩。
- m,n 的相对大小不定,m (> or < or =) n
- rank(A) =rank(A|b)=n (n=rank(X)=A满秩时列向量个数) ,就有唯一解
- rank(A) =rank(A|b)<n (n=rank(X)=A满秩时列向量个数),就有无数解
满秩矩阵有唯一解
定理
有解的判断
对于线性方程组 Ax=b,如果系数矩阵A和秩 = 增广矩阵B(B=A|b)的秩,也就是rank(A) =rank(B)那么就有解
解的个数的判断
对于线性方程组 Ax=b,如果系数矩阵A和秩 = 增广矩阵B(B=A|b)的秩,并且
如果A是m*n的矩阵,其中n是A的列向量的个数。
rank(A) =rank(B)=n (A的列向量的个数) ,就有唯一解
rank(A) =rank(B)<n (A的列向量的个数) ,就有无数解
满秩矩阵有唯一解
————————————————
版权声明:本文为CSDN博主「奔跑的犀牛先生」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/xuemanqianshan/article/details/132522056
7 秩零定理
- Ax=y
- 矩阵Am*n, 而Xn*1=[x1,x2....xn] ,bm*1=[b1,b2....bm]
- rank(x) =n 单个一维向量,不存在线性相关问题,所以 n 代表定义域X的秩
- rank(b)=m 单个一维向量,不存在线性相关问题
- 因此,A的零空间 rank(A)<=min(m,n) ,rank(A) 代表值域的秩,因为值域 rank(b)=m其实被rank(A) 所决定。但是值域的秩,为啥不直接用 rank(b) 呢?
- 而 rank(null(A)) 实际就是 rank(Ax=0),所以 rank(null(A))<=min(m,n)
形式1
- rank(值域)+rank(null(A)) = rank(定义域)
- rank(A)+rank(null(A))=n
形式2
7 秩零定理
对于矩阵Am*n,其中n 是A的列向量个数
形式1
rank(值域)+rank(null(A)) = rank(定义域)
rank(A)+rank(null(A))=n
形式2
rank(定义域)>=rank(值域)
rank(定义域)--rank(null(A))=rank(值域)
n-rank(null(A))=rank(A)
8 其他知识点
文章来源:https://www.toymoban.com/news/detail-676623.html
到了这里,关于线性代数的学习和整理15:线性代数的快速方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!