csdn冷知识：如何在csdn里输入公式或矩阵

9月前作者：奔跑的犀牛先生分类：Toy博客阅读(39) 违法举报

这篇具有很好参考价值的文章主要介绍了csdn冷知识：如何在csdn里输入公式或矩阵。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

1 输入公式

2 输入矩阵

3 如何输入复杂公式

4 如何修改，已经生成的公式

1 输入公式

进入编辑模式
点击右边的菜单：公式
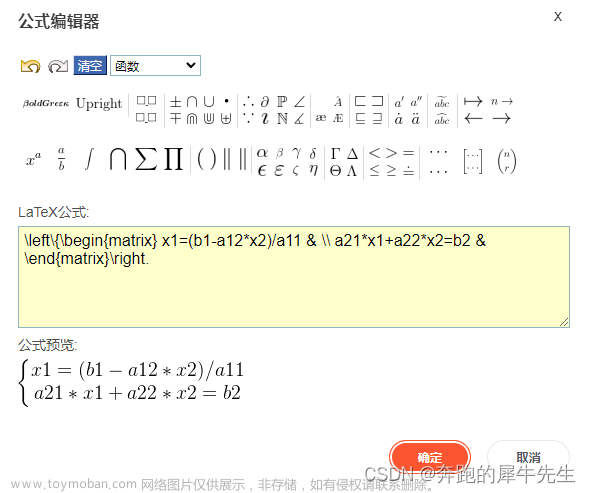
然后进入公式编辑器，选择右边的 ... 可以选择大括号等，右边还有矩阵符号
选择后你需要创建几行几列的格式后
atex 公式会出现格式模板，下面是预览窗口
修改内容，条件非格式内容，或调整格式，就可以输出公式了

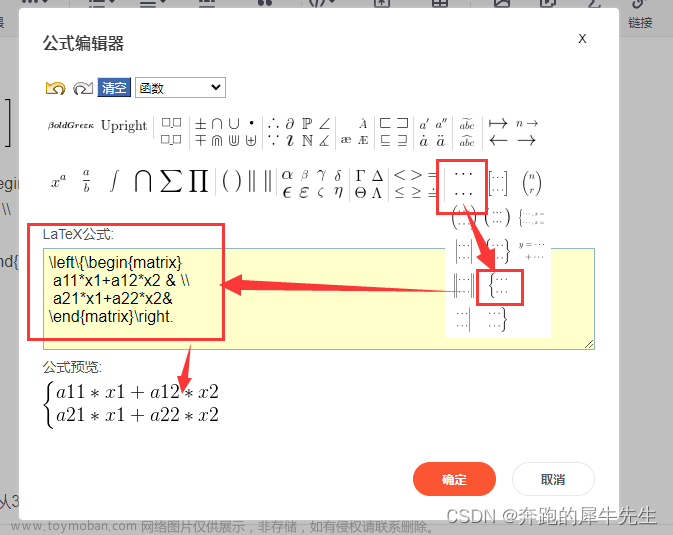
csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数

csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数

csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数

下面是生成的2元一次方程组的公式效果

$csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数$

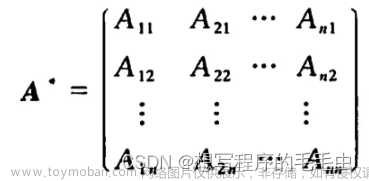
2 输入矩阵

和上面的公式，输入时语法略有不同
每个矩阵的列元素之间用 & 分隔

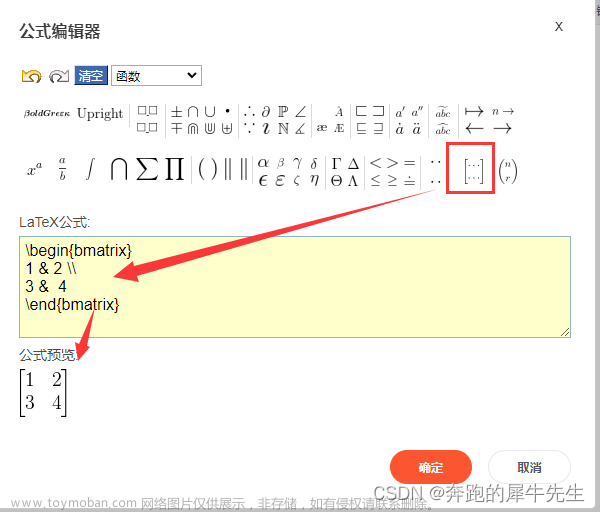
csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数

csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数

下面是生成的2*2的矩阵效果

3 如何输入复杂公式

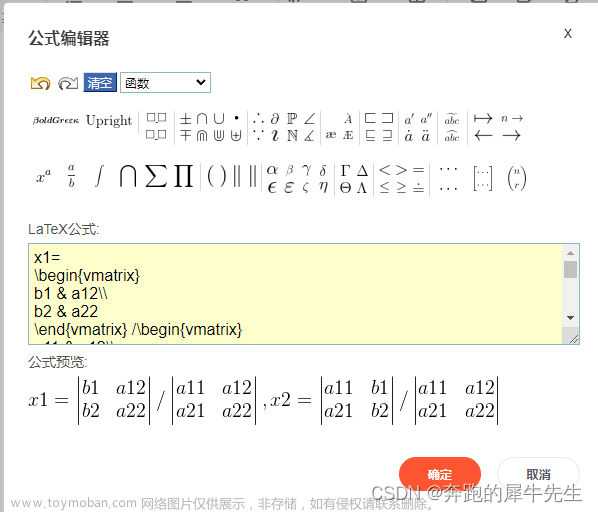
csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数

下面是效果

x1=
\begin{vmatrix} 
b1 & a12\\
b2 & a22 
\end{vmatrix} /\begin{vmatrix} 
a11 & a12\\
a21 & a22 
\end{vmatrix}

,
x2=
\begin{vmatrix} 
a11 & b1\\
a21 & b2 
\end{vmatrix} /\begin{vmatrix} 
a11 & a12\\
a21 & a22 
\end{vmatrix}

4 如何修改已经生成的公式

如果发现输入的公式，需要修改
只需要进入编辑模式，双击公式，即可跳转到编辑窗口

csdn冷知识：如何在csdn里输入公式或矩阵,矩阵,线性代数文章来源地址https://www.toymoban.com/news/detail-677589.html

到了这里，关于csdn冷知识：如何在csdn里输入公式或矩阵的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

【Paddle】PCA线性代数基础 + 领域应用：人脸识别算法（1.1w字超详细：附公式、代码）

🌈你好呀！我是是Yu欸 🌌 2024每日百字篆刻时光，感谢你的陪伴与支持 ~ 🚀 欢迎一起踏上探险之旅，挖掘无限可能，共同成长！主成分分析（PCA，Principal Component Analysis）是一项在高维数据中，寻找最重要特征的降维技术，大大减少数据的维度，而不显著损失信息量。本文

2024年04月28日
浏览(51)
线性代数：线性方程求解、矩阵的逆、线性组合、线性独立

本文参考www.deeplearningbook.org一书第二章2.3 Identity and Inverse Matrices 2.4 Linear Dependence and Span 本文围绕线性方程求解依次介绍矩阵的逆、线性组合、线性独立等线性代数的基础知识点。本文主要围绕求解线性方程展开，我们先把线性方程写出来，方程如下：其中，是已知的；，

2024年02月08日
浏览(54)
线性代数本质系列（一）向量，线性组合，线性相关，矩阵

本系列文章将从下面不同角度解析线性代数的本质，本文是本系列第一篇向量究竟是什么？向量的线性组合，基与线性相关矩阵与线性相关矩阵乘法与线性变换三维空间中的线性变换行列式逆矩阵，列空间，秩与零空间克莱姆法则非方阵点积与对偶性叉积以线性变换

2024年02月04日
浏览(54)
0203逆矩阵-矩阵及其运算-线性代数

定义7 对于 n n n 阶矩阵A，如果有一个 n n n 阶矩阵B，使 A B = B A = E AB=BA=E A B = B A = E 则说矩阵A是可逆的，并把矩阵B称为A的逆矩阵，简称逆阵。定理1 若矩阵A可逆，则 ∣ A ∣ ≠ 0 vert Avert not = 0 ∣ A ∣  = 0 证明： A 可逆，即有 A − 1 ，使得 A A − 1 = E ∣ A A − 1 ∣ = ∣ A

2024年04月13日
浏览(60)
高等代数(七)-线性变换03：线性变换的矩阵

§ 3 § 3 §3 线性变换的矩阵设 V V V 是数域 P P P 上 n n n 维线性空间, ε 1 , ε 2 , ⋯ , ε n varepsilon_{1}, varepsilon_{2}, cdots, varepsilon_{n} ε 1 , ε 2 , ⋯ , ε n 是 V V V 的一组基, 现在我们来建立线性变换与矩阵的关系. 空间 V V V 中任一向量 ξ xi ξ 可以经 ε 1 , ε 2 , ⋯

2024年02月20日
浏览(53)
线性代数｜证明：线性变换在两个基下的矩阵相似

前置定义 1（基变换公式、过渡矩阵）设 α 1 , ⋯ , α n boldsymbol{alpha}_1,cdots,boldsymbol{alpha}_n α 1 , ⋯ , α n 及 β 1 , ⋯ , β n boldsymbol{beta}_1,cdots,boldsymbol{beta}_n β 1 , ⋯ , β n 是线性空间 V n V_n V n 中的两个基， { β 1 = p 11 α 1 + p 21 α 2 + ⋯ + p n 1 α n β 2

2024年02月03日
浏览(54)
【理解线性代数】（四）线性运算的推广与矩阵基础

工业生产的发展趋势总是从单件生产到批量生产。科学技术研究也是一样，总是从简单计算到复合运算、批量运算。批量意味着生产能力、处理能力的提升。计算机从16位发展到64位，从单核发展到多核；计算机从CPU处理数据发展到GPU处理数据；大数据、人工智能领域的大模型

2024年02月09日
浏览(52)
线性代数（4）：伴随矩阵、逆矩阵和矩阵的秩

A 为一个n阶矩阵，行列式 | A | 的每个元素a ij 的代数余子式Aij组成的矩阵叫做伴随矩阵，记作 A* ； a. 如果 A 矩阵可逆，A* = | A | A^-1 b. | A | = | A |^(n-1) c. ( kA )* = k^(n-1) A* a. 若矩阵的行列式结果值不等于 0 ，那么这个矩阵就是

2024年02月08日
浏览(63)
线性代数笔记11--矩阵空间、秩1矩阵

1. 矩阵空间所有的 3 × 3 3 times 3 3 × 3 矩阵构成的空间 M M M 。考虑空间 M M M 的子空间上三角矩阵对称矩阵对角矩阵 3 x 3 3x3 3 x 3 矩阵空间的基: [ 1 0 0 0 0 0 0 0 0 ] [ 0 1 0 0 0 0 0 0 0 ] [ 0 0 1 0 0 0 0 0 0 ] [ 0 0 0 1 0 0 0 0 0 ] [ 0 0 0 0 1 0 0 0 0 ] [ 0 0 0 0 0 1 0 0 0 ] [ 0 0 0 0 0 0 1 0 0 ] [ 0 0 0 0 0 0

2024年03月10日
浏览(48)
0205矩阵分块法-矩阵及其运算-线性代数

1 分块矩阵的定义将矩阵A用若干条纵线和横线分成许多个小矩阵，每一个小矩阵称为A的子快，以子块为元素的形式上的矩阵称为分块矩阵。 2 分块矩阵的运算（性质）设矩阵A与B的行数相同，列数相同，采用相同的分块法，有 A = ( A 11 ⋯ A 1 r ⋮ ⋮ A s 1 ⋯ A s r ) , B = ( B 11 ⋯

2024年04月26日
浏览(39)