时序分解 | MATLAB实现基于SVD奇异值分解的信号分解分量可视化-Toy模板网

这篇具有很好参考价值的文章主要介绍了时序分解 | MATLAB实现基于SVD奇异值分解的信号分解分量可视化。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

时序分解 | MATLAB实现基于SVD奇异值分解的信号分解分量可视化

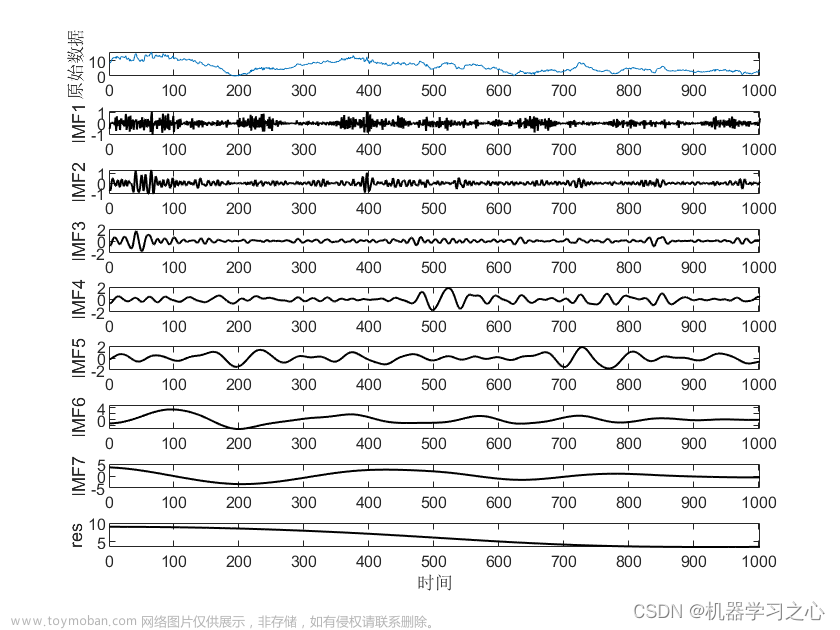
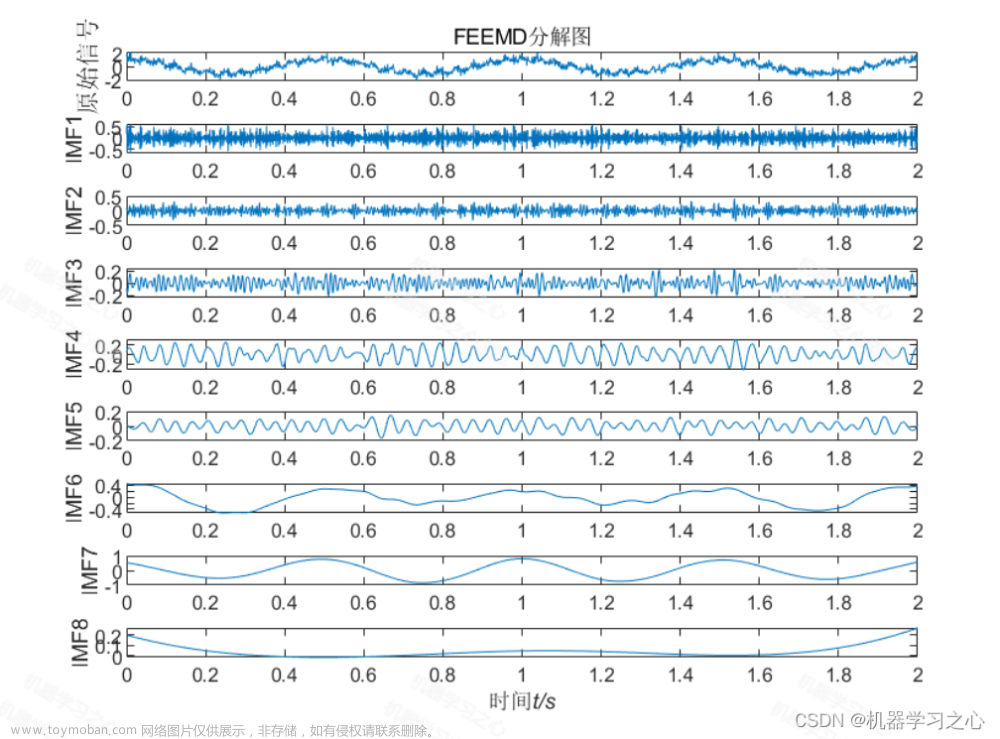
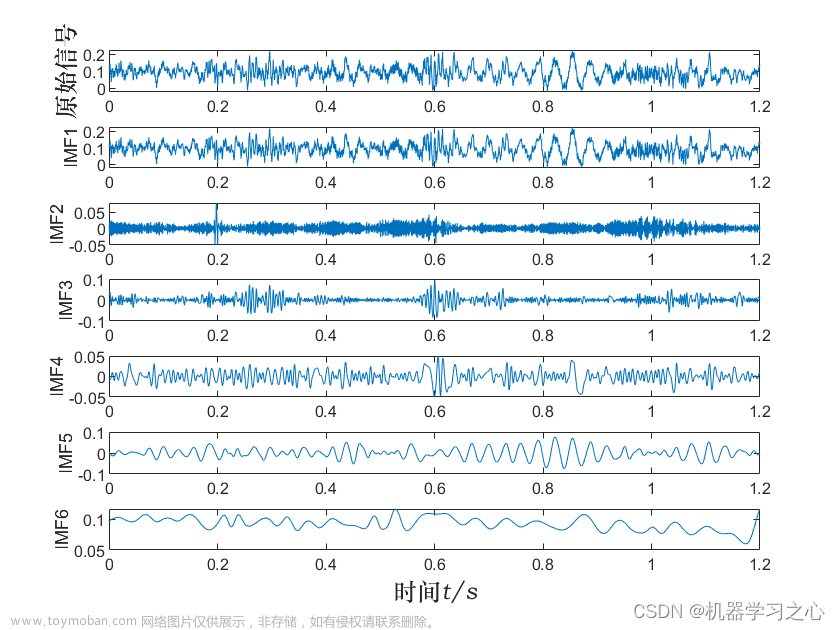
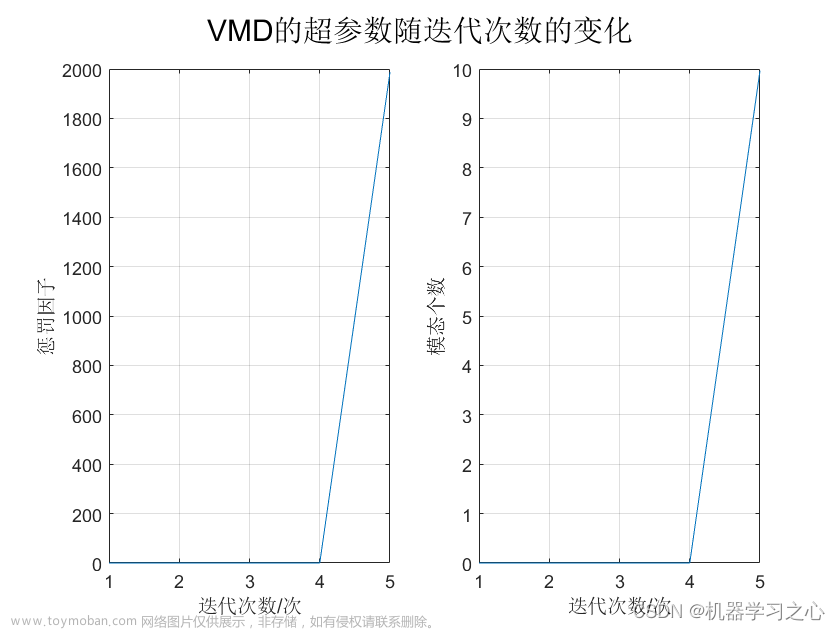
效果一览

时序分解 | MATLAB实现基于SVD奇异值分解的信号分解分量可视化,时序分解,SVD,奇异值分解,信号分解分量可视化

基本介绍

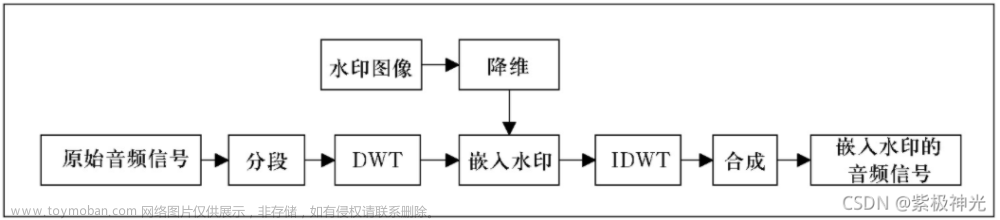
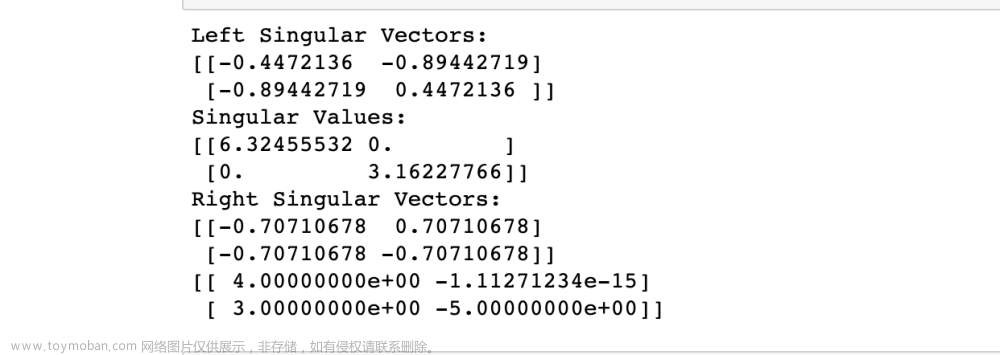
SVD分解重构算法，MATLAB程序，奇异值分解 (Singular Value Decomposition)是一种常见的矩阵分解方法，用于将矩阵分解成三个矩阵的乘积。在信号处理中，SVD 可以用于特征提取、信号降维、图像压缩等方面。SVD 的一个重要应用是主成分分析 (PCA)，可以用于提取数据中的主要特征。
从Excel表格中读取，直接替换数据就可以使用，不需要对程序大幅度改动。程序内有详细注释，便于理解程序运行。。

程序设计

完整源码和数据获取方式：私信回复MATLAB实现基于SVD奇异值分解的信号分解分量可视化。

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

cosD = pdist(meas,'cosine');
clustTreeCos = linkage(cosD,'average');
cophenet(clustTreeCos,cosD)

ans =

    0.9360
[h,nodes] = dendrogram(clustTreeCos,0);
h_gca = gca;
h_gca.TickDir = 'out';
h_gca.TickLength = [.002 0];
h_gca.XTickLabel = [];
————————————————
版权声明：本文为CSDN博主「机器学习之心」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kjm13182345320/article/details/119920826



figure
hidx = cluster(clustTreeCos,'criterion','distance','cutoff',.006);
for i = 1:5
    clust = find(hidx==i);
    plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
    hold on
end
hold off
xlabel('Sepal Length');
ylabel('Sepal Width');
zlabel('Petal Length');
view(-137,10);
grid on

————————————————
版权声明：本文为CSDN博主「机器学习之心」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kjm13182345320/article/details/119920826

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718文章来源地址https://www.toymoban.com/news/detail-678371.html

到了这里，关于时序分解 | MATLAB实现基于SVD奇异值分解的信号分解分量可视化的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！