前面我们讲过当主要结局指标是连续变量时，两总体均数比较时样本量估计的计算公式原理以及PASS软件操作教程。当设计研究的试验因素只有一个，并且该因素的水平数（组数）k≥3，当主要研究指标为连续变量时我们常用单因素多水平方差分析即F检验来考察各组间该研究指标所代表的总体均数之间的差别是否有统计学意义，其样本含量计算公式为：
N为所需的样本含量；σ为标准差，k为组数，μi为各组的平均数，μ平均为各组平均数的平均数，λ为当拒绝总体均数相等的原假设H0时具有非中心F分布的非中心性参数λ（手工计算时可查相关表获得，但PASS15软件中不需要设置该参数）。
本节今天主要讲解采用PASS15软件实现单因素多水平方差分析（F检验）样本含量估计的PASS软件实现。
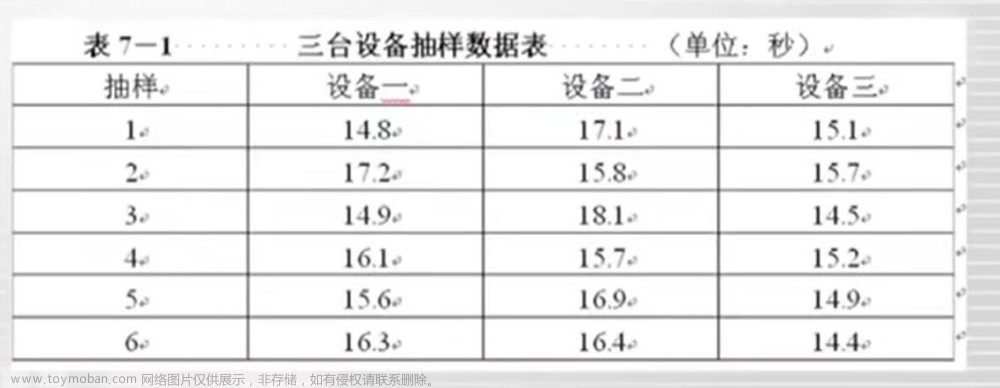
例：某心内科医生欲比较四种不同药品治疗高血压的效果差异。已知四种药品降低收缩压的平均数分别是8.25mmHg、11.75mmHg、12mmHg和13mmHg。假设各药品降低收缩压的标准差都是3.5mmHg。按1:1:1:1平行设计，在α=0.05（双侧检验），β=0.1下，问需要多少调查对象？
解析：本研究只有一个研究因素即组别因素，该因素具有四个水平：四种不同的降压药；主要结局指标是收缩压下降水平值，是连续型变量，四组间的差异性常采用单因素方差分析（F检验）进行检验；目的是进行当四组样本含量相等（等比例平行设计）时总体均数比较（即四均值差异性检验）的样本含量估计。根据题目我们知道了四个参数：①四药品降低收缩压的平均数μ1=8.25mmHg、μ2=11.75mmHg、μ3=12mmHg和μ4=13mmHg；②标准差σ=3.5mmHg；③α=0.05（双侧检验）；④检验效能（1-β）=0.9。
PASS软件样本含量估算的具体步骤：
01 PASS主菜单进入样本含量估算设置界面：
打开PASS15软件，①点击Means菜单并双击或其前面的“＋”展开子菜单栏；→②点击One-Way Designs（ANOVA）菜单并双击或其前面的“＋”展开子菜单栏；→③点击ANOVA F-Test；→④点击有边方框的One-Way Analysis of Variance F-Tests → 弹出 One-Way Analysis of Variance F-Tests 对话框进入单因素方差分析时所需样本含量估计界面，详见操作示意图 1 。
02 PASS样本含量估算参数设置：
①Solve For：Sample Size，首先说明我们本次所求的结果为样本含量；→②Power：0.9，表明检验效能（1-β）为90%；→③Alpha：0.05，表示检验水准为0.05；→④G（Number of Groups）：4，指定研究因素的水平数为4个不同水平；→⑤Group Allocation Ratios：Equal ，表明各组样本例数相等（本例1:1:1:1），也可自定义各组的样本例数之比；→⑥Input σmusing：List of means（μi's）from which σmis calculated ，指定均值的标准差(有“σmvalues directly”和“List of means（μi's) from which σmis calculated”两种形式，当选择前者时只需要直接输入均值的标准差σm，而选择后者时需要输入各组样本的均数，然后PASS软件根据计算公式计算出均值的标准差σm），由于本例知道各样本的均值（μ1=8.25、μ2=11.75、μ3=12和μ4=13mmHg），故选择“List of means（μi's） from which σmis calculated”；说明采用各组的均值计算均值的标准差；→⑦Means（μ1，μ2，...，μG）：8.25 11.75 12 13，指定各样本均数，本例μ1=8.25、μ2=11.75、μ3=12和μ4=13mmHg；→⑧K（Means Multiplier）：1，指定样本均数的乘数（K），当要考虑样本均数变化对样本量影响时可设置多个K值以便观察样本量变化情况，一般采用默认值，即K=1；→⑨σ（Standard Deviation）：3.5，指定总体标准差，可以设置不同的取值以探讨标准差对样本量含量的影响，本例假设各组总体标准差相同即标准差σ=3.5mmHg；→⑩点击Calculate 按钮，完成单因素多水平设计方差分析所需的样本量估算，详见操作示意图（图2）
03 PASS样本含量估算结果：
由图3可知，PASS软件给出的总体率样本量估算的结果同前面进行估计总体均数时样本含量估算结果类似，主要有：样本含量估算的结果、相关参考文献、样本量估算报告中出现各名词的定义、对计算结果的总结描述以及假定脱落率为20%时所需的样本含量估计结果和其各名词的相关定义。由于脱落率不同研究结果各不相同，故本次不看脱落率为20%的相关结果，我们主要关注Total（N）这一结果即可：本研究按1:1:1:1等比例平行设计每组最少需要15例，四组共需要60例研究对象才能发现四组药物间降压效果差异有统计学意义。
文章来源：https://www.toymoban.com/news/detail-678687.html
想要了解更多统计教程相关知识，可以到常笑医学网（www.cxmed.cn）的医学统计栏目进行查询和学习。文章来源地址https://www.toymoban.com/news/detail-678687.html
到了这里，关于统计教程｜PASS实现单因素多水平方差分析的样本含量估计的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
