
👻内容专栏: 《数据结构与算法篇》
🐨本文概括: 利用数据结构栈(Stack)来模拟递归,实现快排的非递归版本;递归版本测试OJ题时,有大量重复元素样例不能通过,导致性能下降,优化快速排序通过将数组划分为三个区域,可以更有效地处理重复元素。
🐼本文作者: 阿四啊
🐸发布时间:2023.8.28
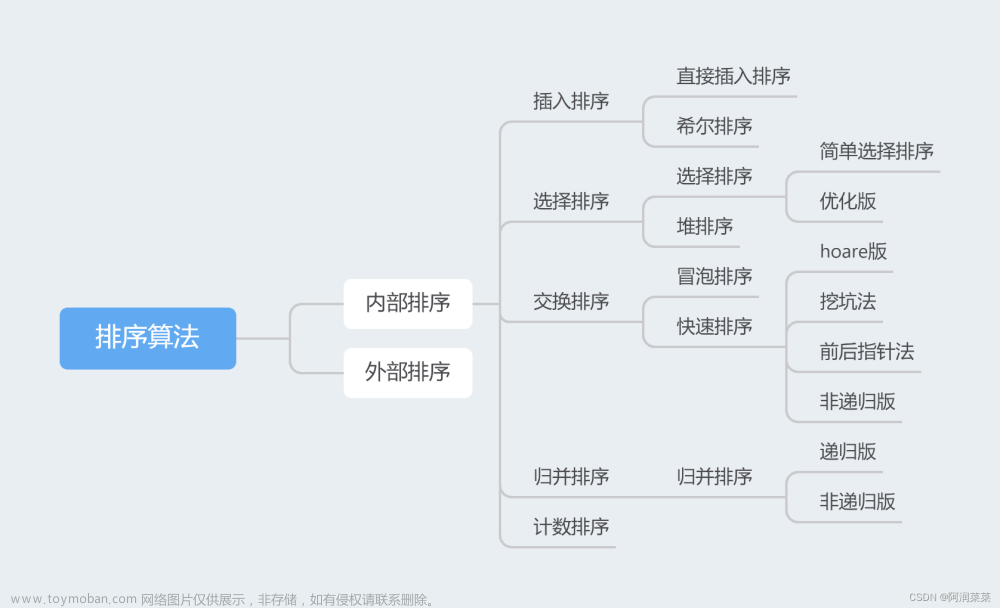
快速排序(非递归)
1.为什么要学习非递归版本?
前面我们使用了三个版本实现快速排序,但都是属于递归类型算法,函数调用会建立函数栈帧,递归深度取决于函数调用的次数。栈空间内存有限,在处理大规模数据集时,递归深度的增加可能导致栈溢出的情况,所以在我们学会了递归版本之后,需要继续强化学习非递归版本,利用之前学习的数据结构栈(Stack)来模拟实现。
2.基本思想
我们知道,我们在写递归版本的时候,快速排序主要处理的是数组的不同区间,将问题分解为较小的子问题并在每个子问题上递归地应用相同的排序算法来完成排序。

那么我们如何使用栈(Stack)来模拟实现呢?
核心思想是使用一个栈来存储待排序的子数组的起始和结束下标。在每次循环中,从栈中弹出一个子数组并执行分区操作(根据基准值(
key),划分区间,这一步骤即递归版本写的Partition函数),选然后根据分区结果将未处理的左右子数组的下标压入栈中,直到栈为空为止。
3.算法分析
👇①:
👇②:
👇③:继续重复以上步骤,直到栈中的数据为空。
4.代码实现
因为涉及到使用栈,而本篇数据结构基于C语言讲解,所以讲自己实现的栈的文件源代码也顺便放在这。
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//hoare版本
int Partition1(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
//注意: 要加上left < right 否则会出现越界
//若不判断等于基准值,也会出现死循环的情况
//右边找小
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左边找大
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}
void QuicksortNonR(int* a, int begin, int end)
{
Stack st;
StackInit(&st);
//注意栈的顺序是后进先出,需要倒着放进去,正着拿出来
//将排序数组的起始和末端下标入栈
StackPush(&st, end);
StackPush(&st, begin);
//栈不为空一直循环
while (!StackEmpty(&st))
{
//弹出子区间(左右两个下标)
int left = StackTop(&st);
StackPop(&st);
int right = StackTop(&st);
StackPop(&st);
//执行分区操作
int keyi = Partition1(a, left, right);
//[left,keyi - 1] keyi [keyi + 1, right]
//注意只剩一个数或区间不存在则停止入栈
if (keyi + 1 < right)
{
StackPush(&st,right);
StackPush(&st,keyi + 1);
}
if (left < keyi - 1)
{
StackPush(&st, keyi - 1);
StackPush(&st, left);
}
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
}
int main()
{
int a[] = { 9,6,7,1,4,5,5,2,10,1,6,3,7 };
QuicksortNonR(a, 0, sizeof a / sizeof(int) - 1);
PrintArray(a, sizeof a / sizeof(int));
}
栈
相关函数声明:
#pragma once
#include <stdio.h>
#include <stdbool.h>
#include <assert.h>
#include <stdlib.h>
typedef int DataType;
typedef struct Stack
{
DataType* a;
int top;
int capacity;
}Stack;
//栈的初始化
void StackInit(Stack* pst);
//入栈
void StackPush(Stack* pst,DataType x);
//出栈
void StackPop(Stack* pst);
//栈的销毁
bool StackEmpty(Stack* pst);
//获取栈顶元素
DataType StackTop(Stack* pst);
//获取栈元素个数
int StackSize(Stack* pst);
//栈的销毁
void StackDestroy(Stack* pst);
相关函数实现:
#define _CRT_SECURE_NO_WARNINGS
#include "stack.h"
//栈的初始化
void StackInit(Stack* pst)
{
assert(pst);
pst->a = NULL;
//pst->top = -1;//栈顶元素的位置
pst->top = 0;//栈顶元素的下一个位置
pst->capacity = 0;
}
//入栈
void StackPush(Stack* pst,DataType x)
{
if (pst->top == pst->capacity)
{
int newCapacity = pst->capacity == 0 ? 4 : (pst->capacity) * 2;
DataType* tmp = (DataType*)realloc(pst->a, sizeof(DataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail\n");
return;
}
else
{
pst->a = tmp;
pst->capacity = newCapacity;
}
}
pst->a[pst->top++] = x;
}
//出栈
void StackPop(Stack* pst)
{
assert(pst);
pst->top--;
}
//判断栈是否为空
bool StackEmpty(Stack* pst)
{
assert(pst);
return pst->top == 0;
}
//获取栈顶元素
DataType StackTop(Stack* pst)
{
return pst->a[pst->top - 1];
}
//获取栈元素个数
int StackSize(Stack* pst)
{
return pst->top;
}
//栈的销毁
void StackDestroy(Stack* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}
总结
时间复杂度:O(N*logN)
空间复杂度:O(logN)
⚠️注意:尽管使用栈实现了递归过程,但栈的使用本质上是在模拟递归调用栈。这种方法可以避免递归深度过大导致栈溢出的问题,并且在一些情况下比递归版本更有效。
递归版本优化(三路划分)
1.缺陷问题:
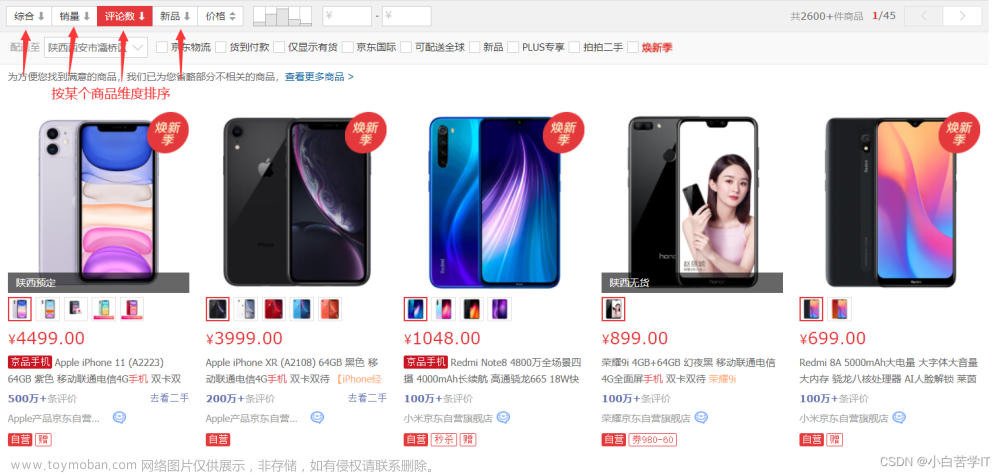
下面给出一道力扣OJ题:👉传送链接:912.排序数组
题目要求就是给定一些数据,将乱序的数组排列为升序。我们用希尔排序、归并排序、堆排序……一般效率较高的都可以跑过,但是唯独快排用递归、非递归都不能跑过!就很离谱,因为快排有名,也就是这题故意针对快排,下面利用写出的递归版本的快排去跑这个OJ。
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//三数取中
int GetMidIndax(int* a,int left, int right)
{
int mid = left + (rand() % (right - left));
if (a[mid] > a[left])
{
if (a[right] > a[mid]) return mid;
else if (a[right] > a[left]) return right;
else return left;
}
else //a[mid] < a[left]
{
if (a[right] < a[mid]) return mid;
else if (a[right] < a[left]) return right;
else return left;
}
}
//hoare版本
int Partition1(int* a, int left, int right)
{
int midi = GetMidIndax(a, left, right);
Swap(&a[left],&a[midi]);
int keyi = left;
while (left < right)
{
//右边找小
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左边找大
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}
//快排(递归版本)
void QuickSort(int* a, int begin, int end)
{
if (begin >= end) return;
int keyi = Partition1(a, begin, end);
//前序遍历
//递归基准值左边的区间
QuickSort(a, begin, keyi - 1);
//递归基准值右边的区间
QuickSort(a, keyi + 1, end);
}
int* sortArray(int* nums, int numsSize, int* returnSize){
QuickSort(nums, 0, numsSize - 1);
*returnSize = numsSize;
return nums;
}
我们发现这题一共21个测试用例,只通过了17个,显示超出时间限制,并且nums里出现了很多2,因为有大量重复元素样例不能通过,这样的基准值key一直是处于数组第一个位置,导致性能下降,出现了最坏的情况,时间复杂度为O(N2) 文章来源:https://www.toymoban.com/news/detail-679060.html
文章来源:https://www.toymoban.com/news/detail-679060.html
2.解决方案:
- [----------------------------------------------------------------------------------------------------------------------------------------]

基本思想:三路划分通过将数组划分为三个部分来解决这个问题:小于、等于和大于基准值的元素。文章来源地址https://www.toymoban.com/news/detail-679060.html
- 用随机值三数取中法选择一个基准值
key。- 定义三个指针变量:
left、cur、right,left的初始值为区间的起始位置,cur指针的初始值为left + 1,right指针的初始值为区间的末尾位置。- 遍历数组,通过与基准值的比较将元素分成三部分:
- 如果当前元素小于
key,将它与left指针所指的位置交换,然后将left指针和cur指针都向右移动。- 如果当前元素等于
key,将cur指针向右移动。- 如果当前元素大于
key,将它与right指针所指的位置交换,然后将right指针向左移动。left指针和right指针之间的区域(包含left和right)即为与key相等的所有元素,然后前序遍历,对left指针左边区域进行递归,right指针右边区域进行递归。- 最终,数组会被划分为三个区域:小于
key区域 、等于key区域 和大于key区域。
3.代码参考
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
int GetMidIndax(int* a,int left, int right)
{
int mid = left + (rand() % (right - left));
if (a[mid] > a[left])
{
if (a[right] > a[mid]) return mid;
else if (a[right] > a[left]) return right;
else return left;
}
else //a[mid] < a[left]
{
if (a[right] < a[mid]) return mid;
else if (a[right] < a[left]) return right;
else return left;
}
}
//三路分割 左 l r 右
void QuickSort(int* a, int begin, int end)
{
if (begin >= end) return;
int left = begin;
int right = end;
int cur = left + 1;
int mid = GetMidIndax(a, begin, end);
Swap(&a[mid],&a[left]);
int key = a[left];
while (cur <= right)
{
if (a[cur] < key)
{
Swap(&a[cur], &a[left]);
left++;
cur++;
}
else if (a[cur] > key)
{
Swap(&a[cur], &a[right]);
right--;
}
else //a[cur] == key
{
cur++;
}
}
// [begin left- 1],[left,right],[right + 1,end]
QuickSort(a, begin, left - 1);
QuickSort(a, right + 1, end);
}
int* sortArray(int* nums, int numsSize, int* returnSize){
srand(time(NULL));
QuickSort(nums, 0, numsSize - 1);
*returnSize = numsSize;
return nums;
}
到了这里,关于【数据结构与算法篇】手撕八大排序算法之快排的非递归实现及递归版本优化(三路划分)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!





![[ 数据结构 -- 手撕排序算法第二篇 ] 冒泡排序](https://imgs.yssmx.com/Uploads/2024/02/501879-1.png)





