第八章 贪心算法 part03 1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果 （day34补）

本文章代码以c++为例！

一、力扣第1005题：K 次取反后最大化的数组和

题目:

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

• 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。

重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

示例 1：

输入：nums = [4,2,3], k = 1
输出：5
解释：选择下标 1 ，nums 变为 [4,-2,3] 。

示例 2：

输入：nums = [3,-1,0,2], k = 3
输出：6
解释：选择下标 (1, 2, 2) ，nums 变为 [3,1,0,2] 。

示例 3：

输入：nums = [2,-3,-1,5,-4], k = 2
输出：13
解释：选择下标 (1, 4) ，nums 变为 [2,3,-1,5,4] 。

提示：

• 1 <= nums.length <= 104
• -100 <= nums[i] <= 100
• 1 <= k <= 104

思路

本题思路其实比较好想了，如何可以让数组和最大呢？

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

局部最优可以推出全局最优。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。

虽然这道题目大家做的时候，可能都不会去想什么贪心算法，一鼓作气，就AC了。

我这里其实是为了给大家展现出来 经常被大家忽略的贪心思路，这么一道简单题，就用了两次贪心！

那么本题的解题步骤为：

• 第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
• 第二步：从前向后遍历，遇到负数将其变为正数，同时K--
• 第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
• 第四步：求和

对应C++代码如下：

class Solution {
static bool cmp(int a, int b) {
    return abs(a) > abs(b);
}
public:
    int largestSumAfterKNegations(vector<int>& A, int K) {
        sort(A.begin(), A.end(), cmp);       // 第一步
        for (int i = 0; i < A.size(); i++) { // 第二步
            if (A[i] < 0 && K > 0) {
                A[i] *= -1;
                K--;
            }
        }
        if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步
        int result = 0;
        for (int a : A) result += a;        // 第四步
        return result;
    }
};

• 时间复杂度: O(nlogn)
• 空间复杂度: O(1)

# 总结

贪心的题目如果简单起来，会让人简单到开始怀疑：本来不就应该这么做么？这也算是算法？我认为这不是贪心？

本题其实很简单，不会贪心算法的同学都可以做出来，但是我还是全程用贪心的思路来讲解。

因为贪心的思考方式一定要有！

如果没有贪心的思考方式（局部最优，全局最优），很容易陷入贪心简单题凭感觉做，贪心难题直接不会做，其实这样就锻炼不了贪心的思考方式了。

所以明知道是贪心简单题，也要靠贪心的思考方式来解题，这样对培养解题感觉很有帮助。

二、力扣第134题：加油站

题目：

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

示例 1:

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

提示:

• gas.length == n
• cost.length == n
• 1 <= n <= 105
• 0 <= gas[i], cost[i] <= 104

思路

# 暴力方法

暴力的方法很明显就是O(n^2)的，遍历每一个加油站为起点的情况，模拟一圈。

如果跑了一圈，中途没有断油，而且最后油量大于等于0，说明这个起点是ok的。

暴力的方法思路比较简单，但代码写起来也不是很容易，关键是要模拟跑一圈的过程。

for循环适合模拟从头到尾的遍历，而while循环适合模拟环形遍历，要善于使用while！

C++代码如下：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        for (int i = 0; i < cost.size(); i++) {
            int rest = gas[i] - cost[i]; // 记录剩余油量
            int index = (i + 1) % cost.size();
            while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈（如果有rest==0，那么答案就不唯一了）
                rest += gas[index] - cost[index];
                index = (index + 1) % cost.size();
            }
            // 如果以i为起点跑一圈，剩余油量>=0，返回该起始位置
            if (rest >= 0 && index == i) return i;
        }
        return -1;
    }
};

问题是：有多个加油站形成一个环形路线，每个加油站都有一个固定的油量（gas数组）和从当前加油站开到下一个加油站所需要的油量（cost数组）。问从哪个加油站出发，可以走完整个环形路线。如果不能从任何一个加油站出发走完整个环形，返回-1。

代码解析：

1. 外层循环：for (int i = 0; i < cost.size(); i++) - 遍历所有加油站，考虑每一个加油站作为起点。

2. int rest = gas[i] - cost[i]; - rest 记录从当前加油站出发后的剩余油量。初始值是当前加油站的油量减去开到下一个加油站所需的油量。

3. int index = (i + 1) % cost.size(); - 初始化一个index，它表示从第i个加油站出发后下一个要到达的加油站的位置。这里使用了取模操作，确保index在数组的范围内。

4. 内层循环：while (rest > 0 && index != i) - 当剩余的油量为正且没有回到起点时，继续模拟行驶。

   • rest += gas[index] - cost[index]; - 更新剩余油量，加上在下一个加油站获得的油量并减去开往再下一个加油站所需的油量。

   • index = (index + 1) % cost.size(); - 移动到下一个加油站。

5. 判断条件：if (rest >= 0 && index == i) - 如果剩余油量不为负且回到了出发的加油站，则找到了一个满足条件的起始位置。

6. 如果所有的加油站都作为起点尝试过后都不能满足条件，返回-1。

这个算法的基本思想是，对于每一个加油站，都尝试从它开始走一圈看是否可行。如果某个加油站作为起点走不通，则说明它到下一个加油站之间的任何一个加油站都不能作为起点。因为如果其中一个可以作为起点，则前一个加油站也可以。所以，当找到一个加油站不能作为起点时，可以直接跳过它到下一个加油站之间的所有加油站，继续尝试下一个。

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

# 贪心算法（方法一）

直接从全局进行贪心选择，情况如下：

• 情况一：如果gas的总和小于cost总和，那么无论从哪里出发，一定是跑不了一圈的

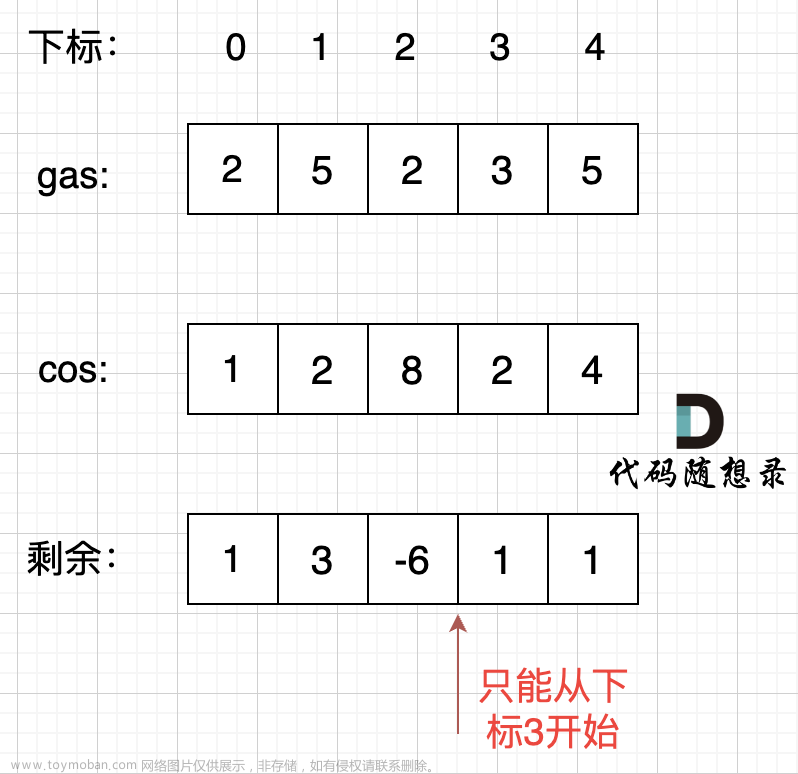
• 情况二：rest[i] = gas[i]-cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。

• 情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能把这个负数填平，能把这个负数填平的节点就是出发节点。

C++代码如下：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int min = INT_MAX; // 从起点出发，油箱里的油量最小值
        for (int i = 0; i < gas.size(); i++) {
            int rest = gas[i] - cost[i];
            curSum += rest;
            if (curSum < min) {
                min = curSum;
            }
        }
        if (curSum < 0) return -1;  // 情况1
        if (min >= 0) return 0;     // 情况2
                                    // 情况3
        for (int i = gas.size() - 1; i >= 0; i--) {
            int rest = gas[i] - cost[i];
            min += rest;
            if (min >= 0) {
                return i;
            }
        }
        return -1;
    }
};

这是一个优化版本的解决方案，用于解决同样的「加油站环形路线」问题。这个版本的算法使用了贪心的思想，通过一次遍历来确定从哪个加油站出发可以完成整个环形路线。

代码解析：

1. 初始化两个变量：

   • curSum：用于记录从起点出发，油箱里的油量累计值。
   • min：用于记录从起点出发，油箱里的油量最小值。

2. 第一个循环：for (int i = 0; i < gas.size(); i++) - 遍历所有加油站，计算从起点出发到每个加油站的油量累计值，并更新curSum和min。

3. if (curSum < 0) return -1; - 如果curSum为负，说明油的总量不足以支撑整个环形路线，直接返回-1。

4. if (min >= 0) return 0; - 如果min为非负，说明从第0个加油站出发，油箱里的油量始终为非负，因此可以从第0个加油站出发完成整个环形路线。

5. 第二个循环：for (int i = gas.size() - 1; i >= 0; i--) - 如果上述两种情况都不满足，从最后一个加油站开始反向遍历。这是因为，如果从第0个加油站出发在某个加油站油量最少（即min），那么从这个加油站的下一个加油站出发可能是一个合适的起点。

6. 在第二个循环中，每次都更新min的值，并检查min是否为非负。如果为非负，说明从当前加油站出发可以完成整个环形路线。

7. 如果所有的加油站都尝试过后都不满足条件，返回-1。

这个算法的基本思想是，首先检查总的油量是否足够支撑整个环形路线，然后找到从哪个加油站出发油箱里的油量最少。如果这个最小值为非负，说明可以从第0个加油站出发；否则，从这个最小值对应的加油站的下一个加油站开始尝试，直到找到一个合适的起点或者遍历完所有的加油站。

• 时间复杂度：O(n)
• 空间复杂度：O(1)

其实我不认为这种方式是贪心算法，因为没有找出局部最优，而是直接从全局最优的角度上思考问题。

但这种解法又说不出是什么方法，这就是一个从全局角度选取最优解的模拟操作。

所以对于本解法是贪心，我持保留意见！

但不管怎么说，解法毕竟还是巧妙的，不用过于执着于其名字称呼。

# 贪心算法（方法二）

可以换一个思路，首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

如图：

那么为什么一旦[0，i] 区间和为负数，起始位置就可以是i+1呢，i+1后面就不会出现更大的负数？

如果出现更大的负数，就是更新i，那么起始位置又变成新的i+1了。

那有没有可能 [0，i] 区间 选某一个作为起点，累加到 i这里 curSum是不会小于零呢？ 如图：

如果 curSum<0 说明 区间和1 + 区间和2 < 0， 那么 假设从上图中的位置开始计数curSum不会小于0的话，就是 区间和2>0。

区间和1 + 区间和2 < 0 同时 区间和2>0，只能说明区间和1 < 0， 那么就会从假设的箭头初就开始从新选择其实位置了。

那么局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。

局部最优可以推出全局最优，找不出反例，试试贪心！

C++代码如下：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int totalSum = 0;
        int start = 0;
        for (int i = 0; i < gas.size(); i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {   // 当前累加rest[i]和 curSum一旦小于0
                start = i + 1;  // 起始位置更新为i+1
                curSum = 0;     // curSum从0开始
            }
        }
        if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
        return start;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

说这种解法为贪心算法，才是有理有据的，因为全局最优解是根据局部最优推导出来的。

# 总结

对于本题首先给出了暴力解法，暴力解法模拟跑一圈的过程其实比较考验代码技巧的，要对while使用的很熟练。

然后给出了两种贪心算法，对于第一种贪心方法，其实我认为就是一种直接从全局选取最优的模拟操作，思路还是很巧妙的，值得学习一下。

对于第二种贪心方法，才真正体现出贪心的精髓，用局部最优可以推出全局最优，进而求得起始位置。

三、力扣第135题：分发糖果

题目：

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。
• 相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示：

• n == ratings.length
• 1 <= n <= 2 * 104
• 0 <= ratings[i] <= 2 * 104

思路

这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼。

先确定右边评分大于左边的情况（也就是从前向后遍历）

此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果，全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果

局部最优可以推出全局最优。

如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个，所以贪心：candyVec[i] = candyVec[i - 1] + 1

代码如下：

// 从前向后
for (int i = 1; i < ratings.size(); i++) {
    if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}

如图：

再确定左孩子大于右孩子的情况（从后向前遍历）

遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？

因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果，所以 要从后向前遍历。

如果从前向后遍历，rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图：

所以确定左孩子大于右孩子的情况一定要从后向前遍历！

如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。

那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。

局部最优可以推出全局最优。

所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多，也比右边candyVec[i + 1]的糖果多。

如图：

所以该过程代码如下：

// 从后向前
for (int i = ratings.size() - 2; i >= 0; i--) {
    if (ratings[i] > ratings[i + 1] ) {
        candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
    }
}

整体代码如下：

class Solution {
public:
    int candy(vector<int>& ratings) {
        vector<int> candyVec(ratings.size(), 1);
        // 从前向后
        for (int i = 1; i < ratings.size(); i++) {
            if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
        }
        // 从后向前
        for (int i = ratings.size() - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1] ) {
                candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
            }
        }
        // 统计结果
        int result = 0;
        for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];
        return result;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(n)

# 总结

这在leetcode上是一道困难的题目，其难点就在于贪心的策略，如果在考虑局部的时候想两边兼顾，就会顾此失彼。

那么本题我采用了两次贪心的策略：

• 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
• 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。

这样从局部最优推出了全局最优，即：相邻的孩子中，评分高的孩子获得更多的糖果。

day34补文章来源地址https://www.toymoban.com/news/detail-679937.html

到了这里，关于第八章 贪心算法 part03 1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果 （day34补）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！