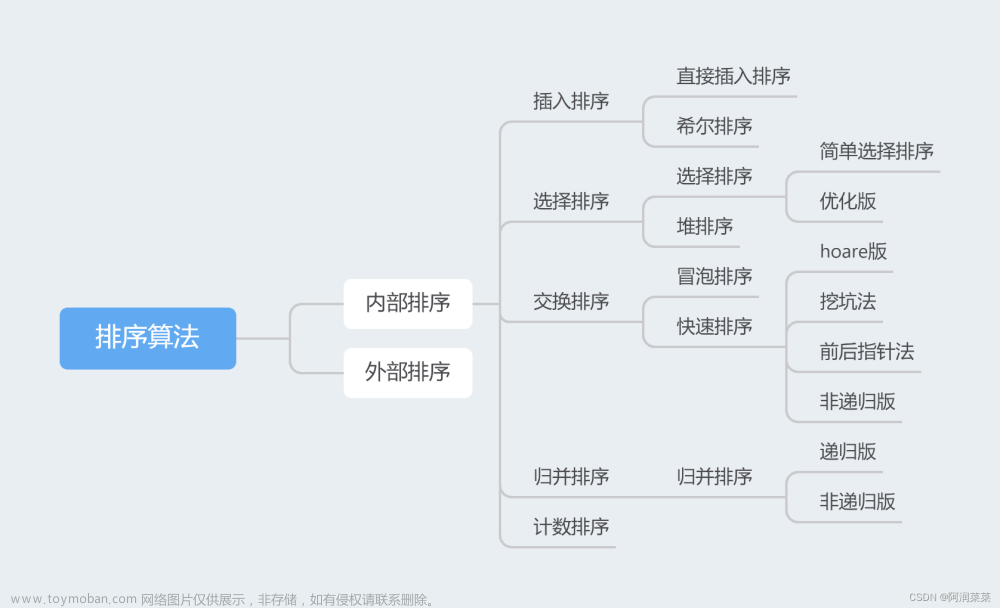
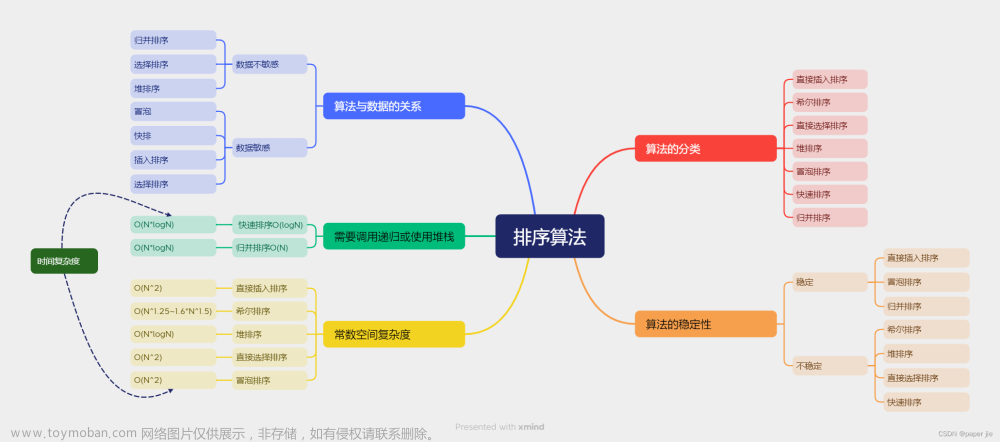
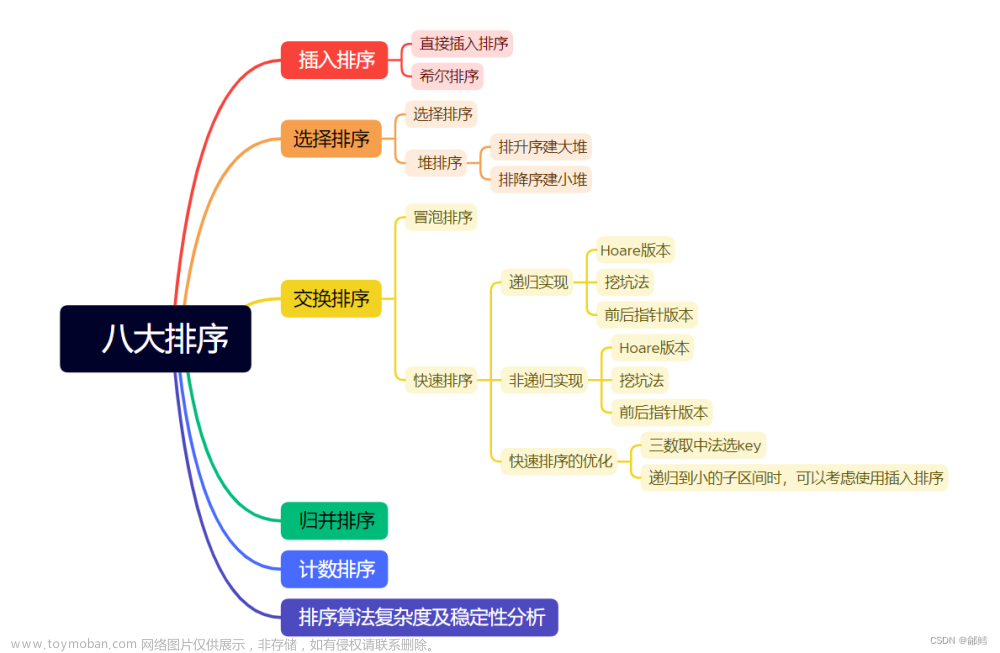
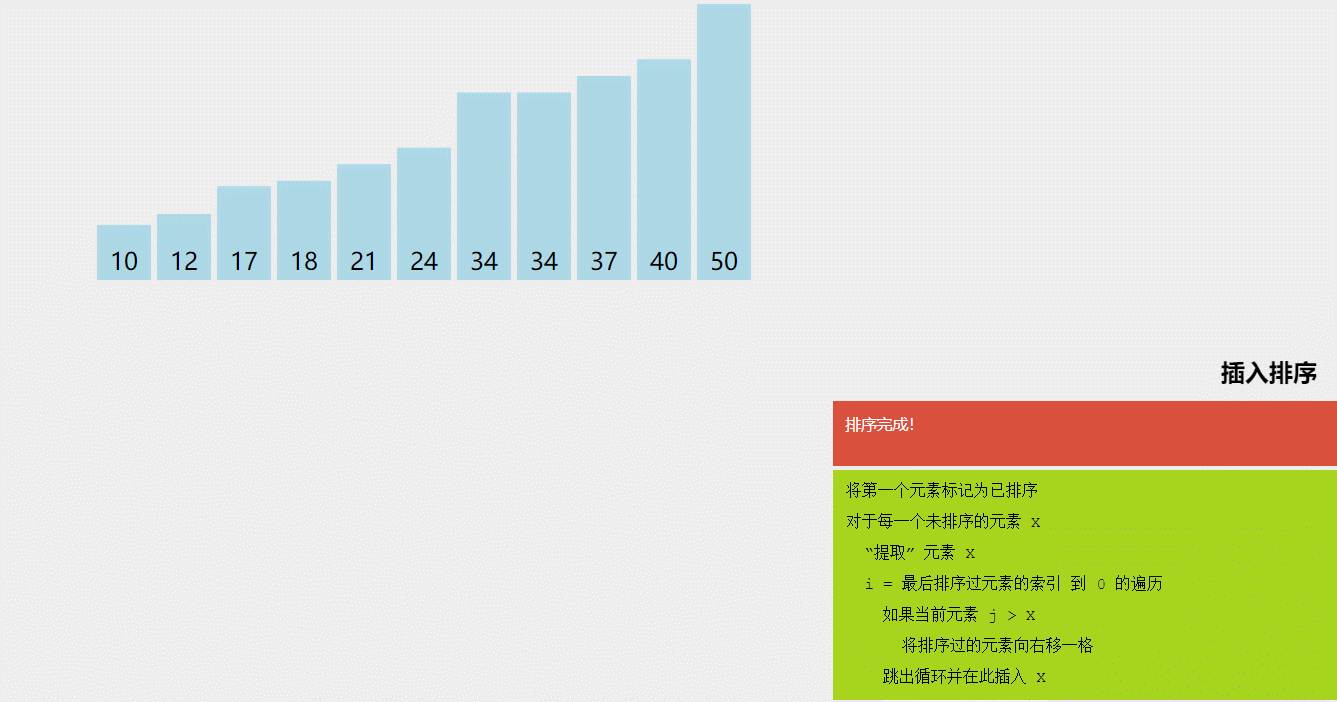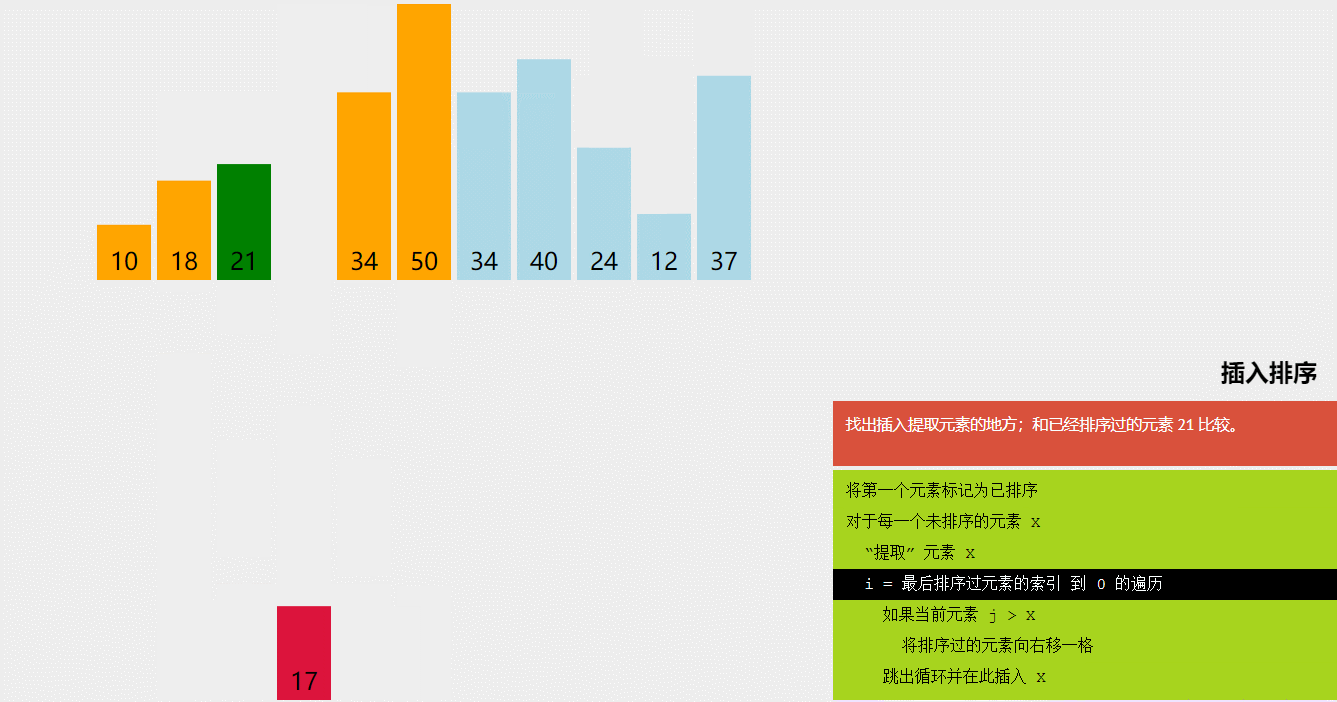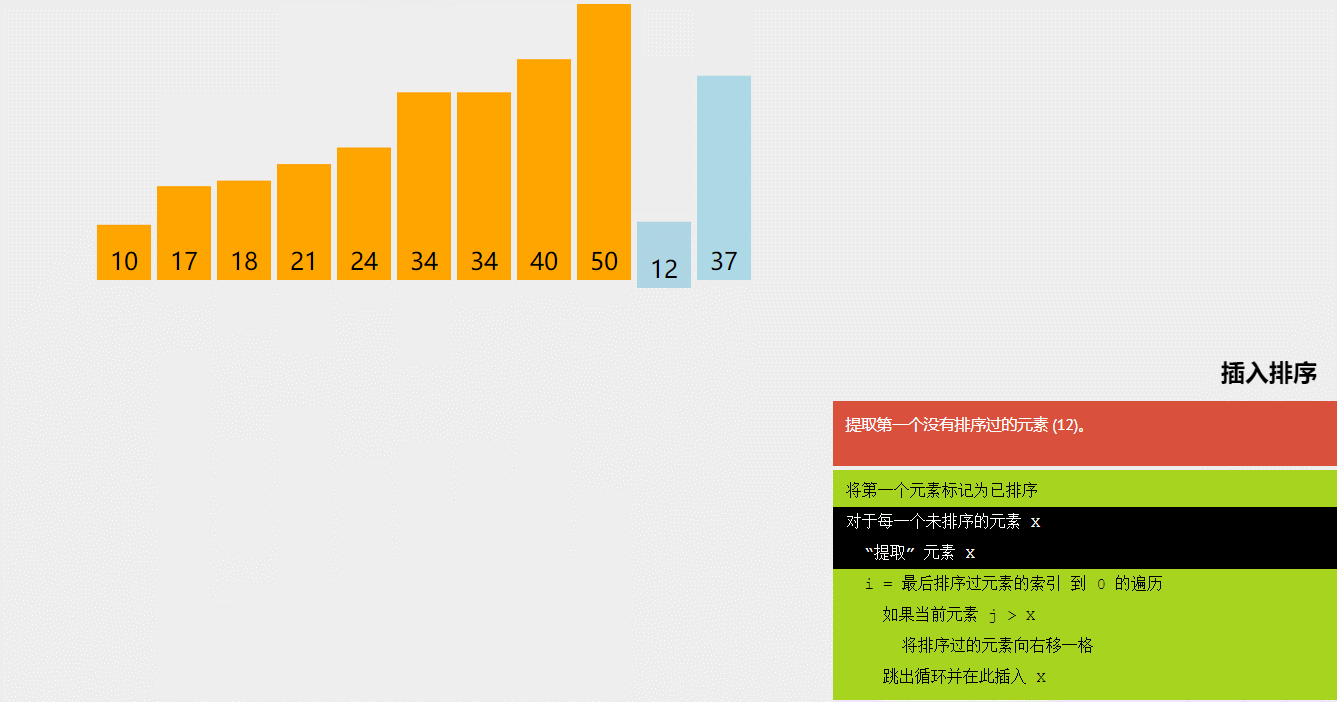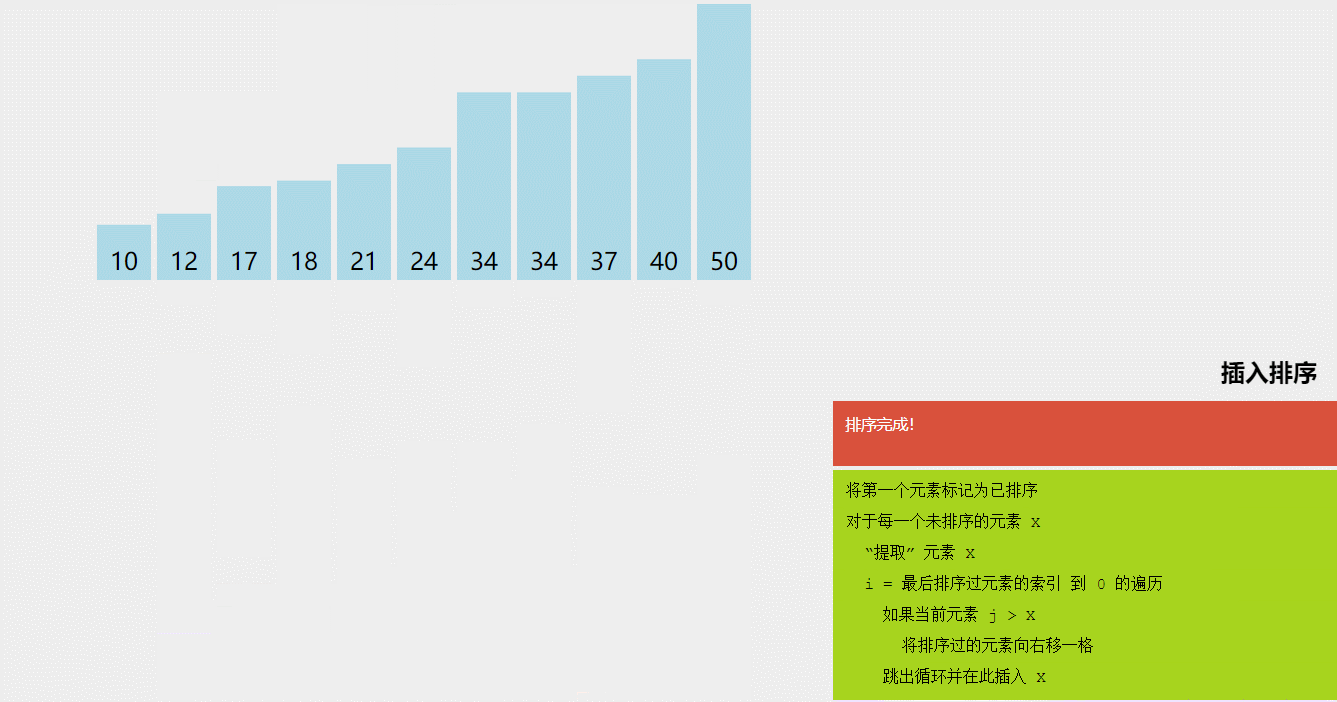
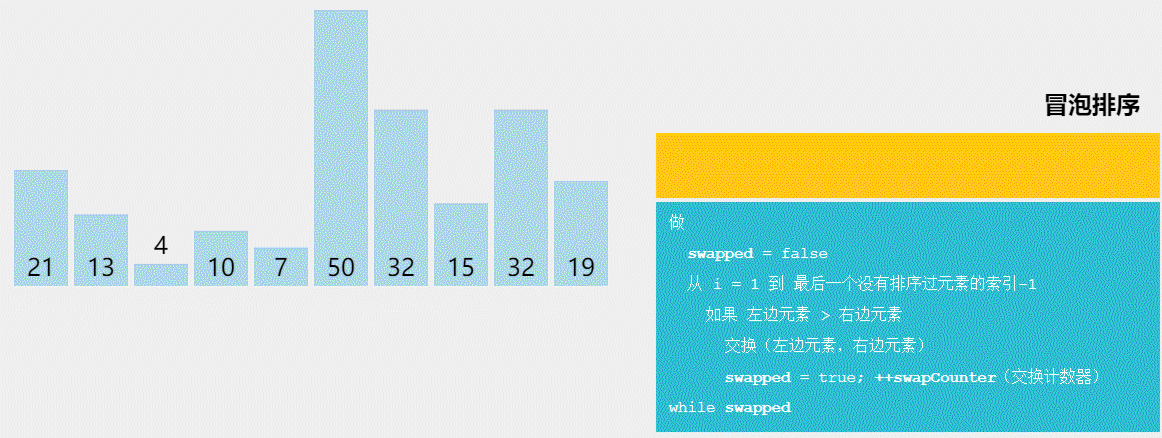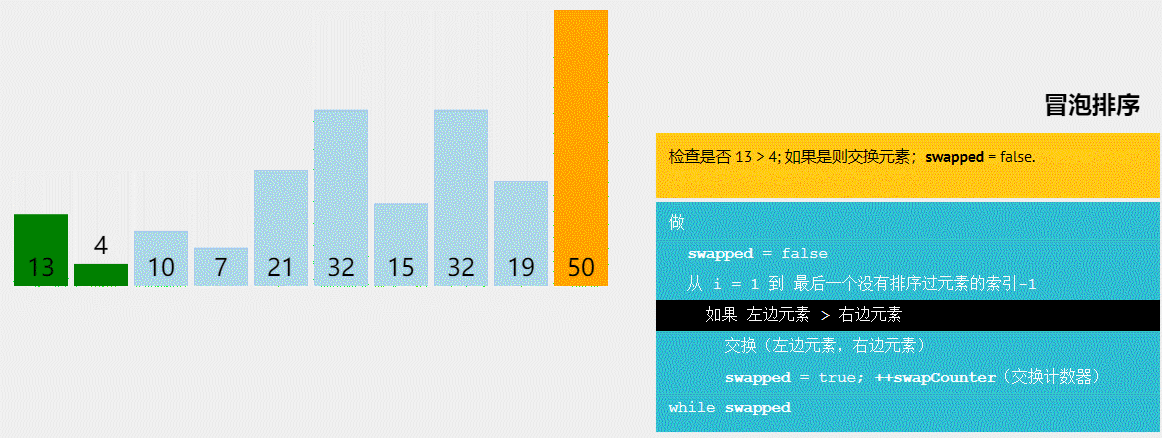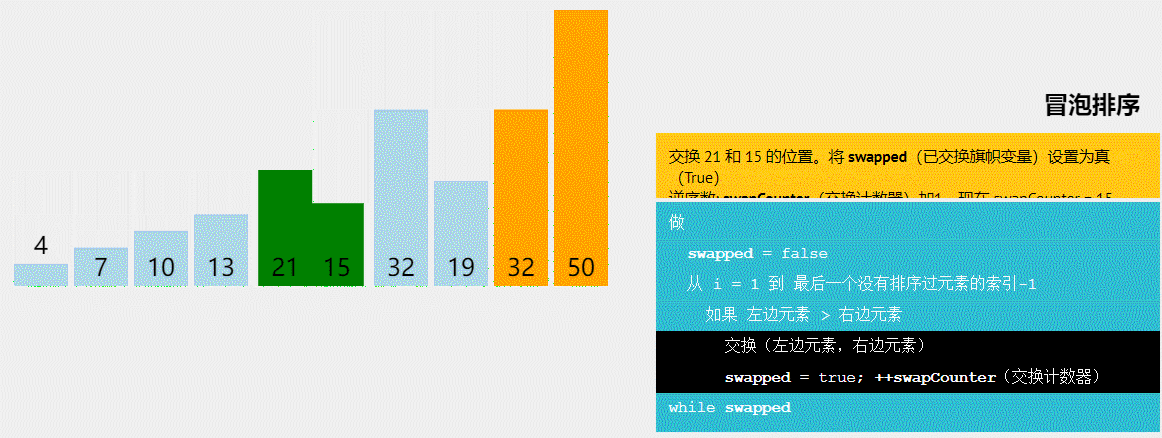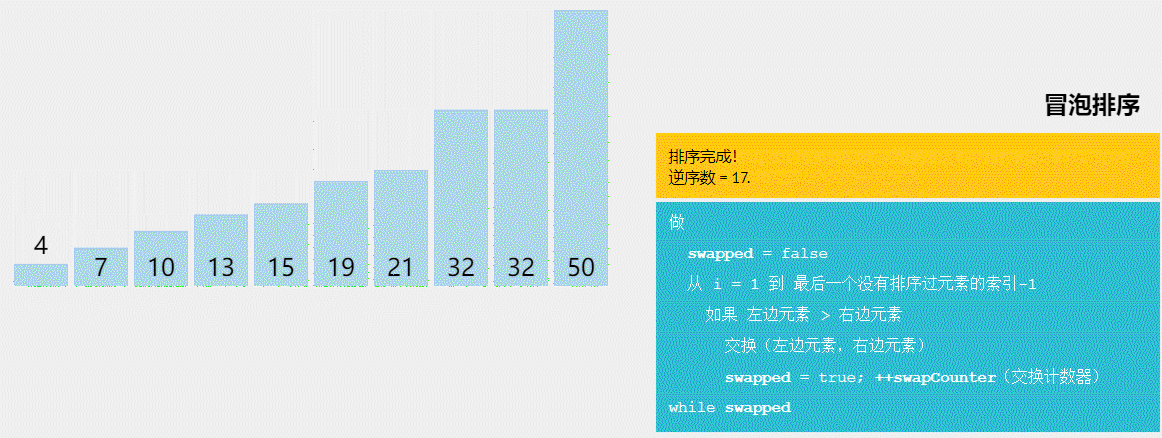【算法】经典的八大排序算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法】经典的八大排序算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

点击链接可视化排序动态演示各个排序算法来加深理解，大致如下

一，冒泡排序（Bubble Sort）

原理

冒泡排序（Bubble Sort）是一种简单的排序算法，它通过多次比较和交换相邻元素的方式，将最大（或最小）的元素逐步冒泡到数组的一端。每一轮冒泡将会将未排序部分中最大（或最小）的元素“浮”到正确的位置。

算法步骤

从数组的第一个元素开始，依次比较相邻的两个元素。

如果前一个元素比后一个元素大（或小，取决于排序顺序），则交换这两个元素。

继续向后遍历，对每一对相邻元素重复步骤 2。

重复步骤 1 到 3，直到没有元素需要交换，整个数组就是有序的。

算法实现
#include <iostream>
#include <vector>

// 冒泡排序
void bubbleSort(std::vector<int>& arr) {
    int n = arr.size();
    
    for (int i = 0; i < n - 1; ++i) {
        // 在每一轮中，比较相邻元素并交换
        for (int j = 0; j < n - i - 1; ++j) {
            if (arr[j] > arr[j + 1]) {
                std::swap(arr[j], arr[j + 1]);
            }
        }
    }
}
性能分析

时间复杂度：

冒泡排序的时间复杂度在最坏和平均情况下都为 O(n^2)，其中 n 是待排序元素的数量。每次遍历需要进行 n-1 次比较，而需要执行 n-1 次遍历。

最好情况下，如果列表本身已经有序，冒泡排序仍然需要进行 n-1 次遍历，但由于没有发生交换，每次遍历只需要进行 n-1、n-2、...、2、1 次比较，时间复杂度为 O(n)。

空间复杂度：
冒泡排序的空间复杂度为 O(1)，只需要常数级别的额外空间。

稳定性：
冒泡排序是稳定的排序算法，因为它在相邻元素比较时仅在必要时才进行交换。

二，选择排序（Selection Sort）

原理

选择排序（Selection Sort）是一种简单的排序算法，它将待排序数组分为已排序和未排序两部分，然后从未排序部分选择最小（或最大）的元素，与已排序部分的最后一个元素交换位置。每次交换都会将一个元素归位，直到整个数组有序。

算法步骤

初始时，将整个序列分为已排序和未排序两部分，已排序为空，未排序包含所有元素。

在未排序部分中，找到最小（或最大）的元素。

将找到的最小元素与未排序部分的第一个元素交换位置，将其放到已排序部分的末尾。

重复执行步骤 2 和 3，直到未排序部分为空，整个序列变得有序。

算法实现
#include <iostream>
#include <vector>

// 选择排序
void selectionSort(std::vector<int>& arr) {
    int n = arr.size();
    
    for (int i = 0; i < n - 1; ++i) {
        int minIndex = i; // 记录最小元素的索引
        
        // 在未排序部分找到最小元素的索引
        for (int j = i + 1; j < n; ++j) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        
        // 将最小元素与当前位置交换
        std::swap(arr[i], arr[minIndex]);
    }
}
性能分析

时间复杂度：
选择排序的时间复杂度在最好、最坏和平均情况下都是 O(n^2)，其中 n 是待排序元素的数量。

空间复杂度：
选择排序的空间复杂度为 O(1)，只需要常数级别的额外空间。

稳定性：
选择排序是不稳定的排序算法，因为在选择最小（或最大）元素的过程中，相同值的元素可能会交换位置。

三，插入排序（Insertion Sort）

原理

插入排序（Insertion Sort）是一种简单的排序算法，它将待排序数组分为已排序和未排序两部分，然后逐个将未排序部分的元素插入到已排序部分的正确位置，使得已排序部分始终保持有序。

算法步骤

初始时，将第一个元素视为已排序部分，其余元素视为未排序部分。

从未排序部分中取出一个元素，将其插入到已排序部分的适当位置，使得插入后的已排序部分仍然保持有序。

重复步骤 2，直到未排序部分为空，整个序列变得有序。

算法实现
#include <iostream>
#include <vector>

// 插入排序
void insertionSort(std::vector<int>& arr) {
    int n = arr.size();
    
    for (int i = 1; i < n; ++i) {
        int current = arr[i]; // 当前要插入的元素
        int j = i - 1; // 已排序部分的末尾索引
        
        // 将元素插入到正确位置
        while (j >= 0 && arr[j] > current) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = current;
    }
}
性能分析

时间复杂度：
插入排序的时间复杂度在最好情况下是 O(n)，最坏和平均情况下是 O(n^2)，其中 n 是待排序元素的数量。

空间复杂度：
插入排序的空间复杂度为 O(1)，只需要常数级别的额外空间。

稳定性：
插入排序是稳定的排序算法，因为它在插入元素时相同值的元素不会改变相对顺序。

四，希尔排序（Shell Sort）

原理

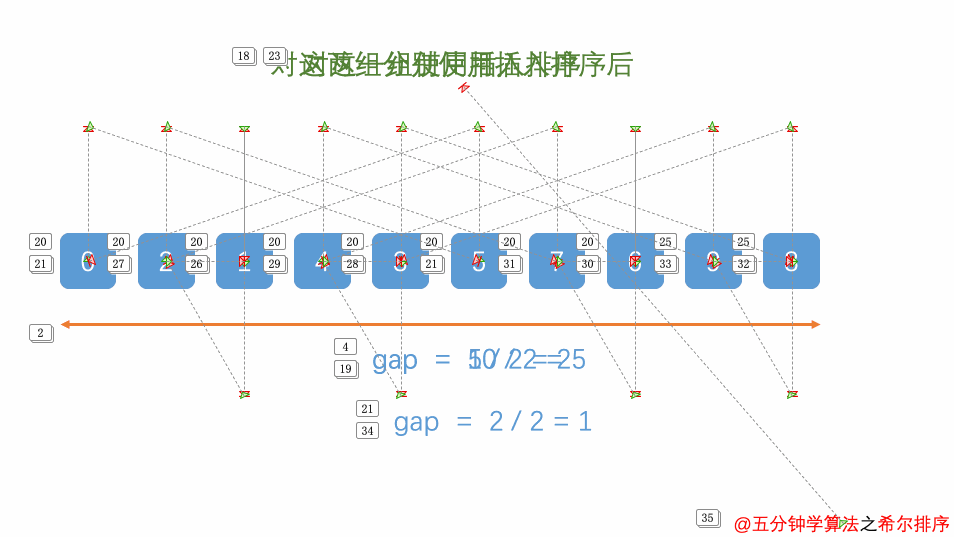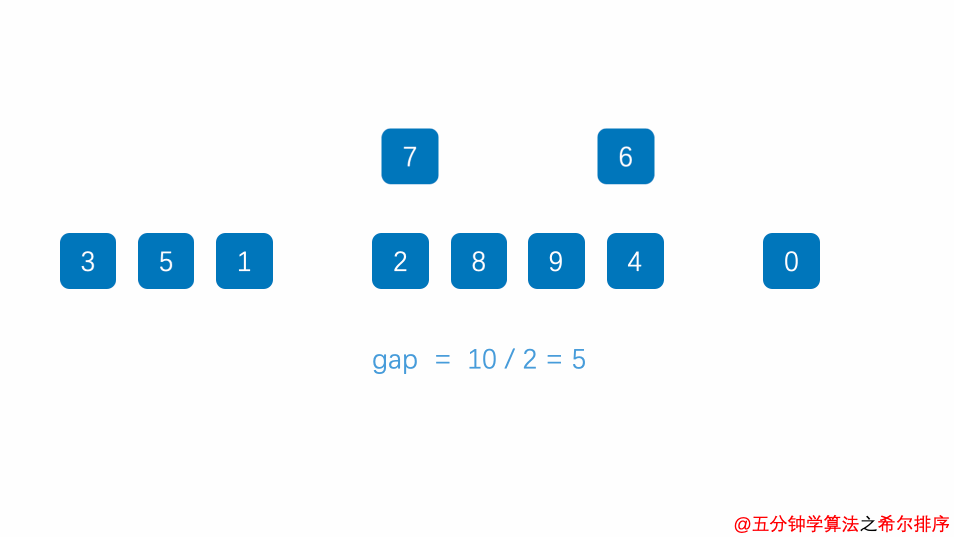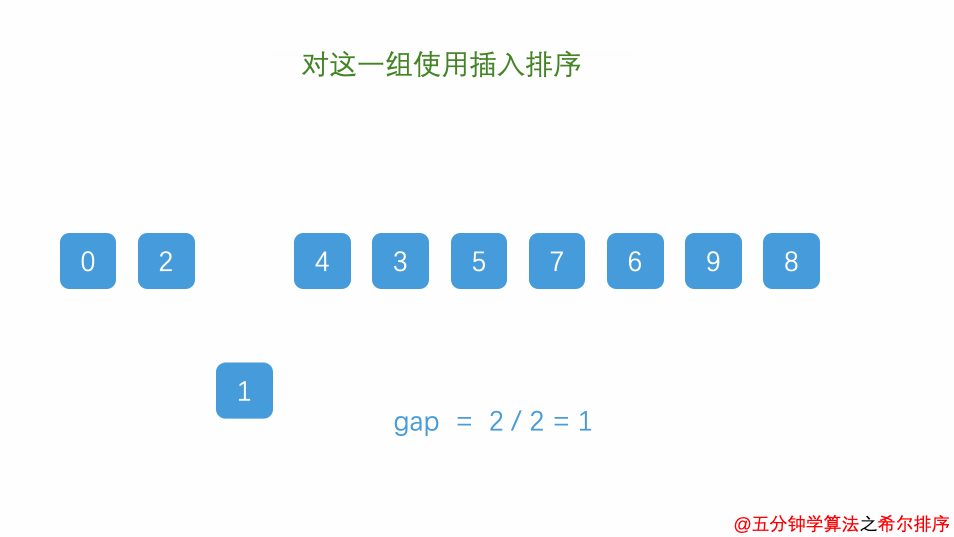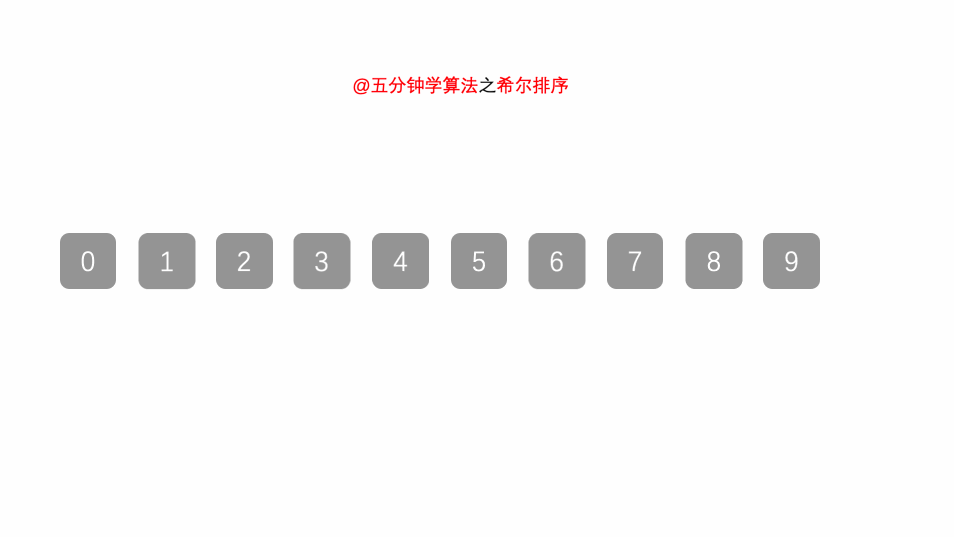
希尔排序（Shell Sort）是一种改进的插入排序算法，它通过将数组分成多个子序列来排序，然后逐步缩小子序列的间隔，最终将整个数组排序。希尔排序的核心思想是使数组中任意间隔 h 的元素都是有序的，当 h 逐步减小到 1 时，整个数组变为有序。

算法步骤

选择一个增量序列（通常为递减的整数序列），例如 [n/2, n/4, n/8, ...]，其中 n 是数组的长度。

对每个增量进行迭代，将数组分成多个子数组，每个子数组中的元素间隔为增量。

对每个子数组进行插入排序，将子数组中的元素插入到已排序部分的适当位置。

重复步骤 2 和 3，不断减小增量，直到增量为 1，此时整个数组被视为一个子数组，进行最后一次插入排序。

算法实现
#include <iostream>

void shellSort(int arr[], int n) {
    for (int gap = n / 2; gap > 0; gap /= 2) {
        // 使用插入排序对子数组进行排序
        for (int i = gap; i < n; ++i) {
            int temp = arr[i];
            int j = i;
            
            // 移动元素，寻找插入位置
            while (j >= gap && arr[j - gap] > temp) {
                arr[j] = arr[j - gap];
                j -= gap;
            }
            
            arr[j] = temp; // 将元素插入到合适的位置
        }
    }
}
性能分析

时间复杂度：
希尔排序的时间复杂度依赖于所选的增量序列。最好的已知增量序列的时间复杂度是 O(n^1.3)，平均情况下的时间复杂度较难分析，但它通常优于 O(n^2) （介于 O(n log n) 和 O(n^2) 之间）的插入排序。具体取决于增量序列的选择。

空间复杂度：
希尔排序的空间复杂度为 O(1)，只需要常数级别的额外空间。

稳定性：
希尔排序不是稳定的排序算法，因为在交换元素的过程中可能会改变相同值元素的相对顺序。

五，归并排序（Merge Sort）

原理

归并排序（Merge Sort）是一种分治策略的排序算法，它将待排序数组不断划分为两个子数组，然后将这些子数组逐步合并成一个有序数组。归并排序的核心思想是将两个有序的子数组合并成一个有序的数组，这样逐步合并，最终得到整个数组有序。

算法步骤

分割：将待排序数组递归地分割成较小的子数组，直到每个子数组只包含一个元素。

合并：将两个有序的子数组合并成一个有序数组。合并过程中，分别从两个子数组中取出较小的元素，放入结果数组中。

算法实现
#include <iostream>
#include <vector>

// 合并两个有序子数组
void merge(std::vector<int>& arr, int left, int mid, int right) {
    int leftCount = mid - left + 1;    // 左边子数组大小
    int rightCount = right - mid;      // 右边子数组大小
    
    // 创建临时数组存放两个子数组的元素
    std::vector<int> leftArr(leftCount), rightArr(rightCount);
    for (int i = 0; i < leftCount; ++i)
        leftArr[i] = arr[left + i];
    for (int i = 0; i < rightCount; ++i)
        rightArr[i] = arr[mid + 1 + i];
    
    // 合并两个子数组
    int i = 0, j = 0, k = left;
    while (i < leftCount && j < rightCount) {
        if (leftArr[i] <= rightArr[j]) {
            arr[k++] = leftArr[i++];
        } else {
            arr[k++] = rightArr[j++];
        }
    }
    
    // 将剩余的元素拷贝到结果数组中
    while (i < leftCount) {
        arr[k++] = leftArr[i++];
    }
    while (j < rightCount) {
        arr[k++] = rightArr[j++];
    }
}

// 归并排序
void mergeSort(std::vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        // 递归地对左右子数组进行排序
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        // 合并两个有序子数组
        merge(arr, left, mid, right);
    }
}
性能分析

时间复杂度：
归并排序的时间复杂度是稳定的，无论数据的分布如何，都是 O(n log n)，其中 n 是待排序元素的数量。

空间复杂度：
归并排序需要额外的空间来存储临时数组，因此其空间复杂度是 O(n)。

稳定性：
归并排序是稳定的排序算法，因为在合并两个子数组时，相同值的元素不会改变相对顺序。

六，快速排序（Quick Sort）

原理

快速排序（Quick Sort）是一种基于分治思想的排序算法，它通过选择一个基准元素，将数组划分为小于基准和大于基准的两部分，然后递归地对这两部分进行排序。在每一次划分后，基准元素会被放置在最终的正确位置上。

算法步骤

选择基准元素：从数组中选择一个基准元素，通常选择第一个或最后一个元素。

分区：将数组划分为小于基准和大于基准的两部分，使得基准元素位于正确的位置上。

递归排序：对小于基准和大于基准的两部分分别递归地应用快速排序算法。

合并：不需要合并步骤，因为在分区过程中已经将数组划分为有序的部分。

算法实现
#include <iostream>
#include <vector>

// 分区函数，返回基准元素的正确位置
int partition(std::vector<int>& arr, int low, int high) {
    int pivot = arr[low]; // 选择第一个元素作为基准
    while (low < high)
    {
        while (low<high && arr[high]>=pivot)--high;
        arr[low] = arr[high];   // 将小于基准的元素移到左边
        while (low<high && arr[low]<=pivot)++low;
        arr[high] = arr[low];   // 将大于基准的元素移到右边
    }

    // 将基准元素放到正确的位置上
    arr[low] = pivot;
    return low; // 返回存放基准的最终位置
}

// 快速排序
void quickSort(std::vector<int>& arr, int low, int high) {
    if (low < high) {
        int pivotIndex = partition(arr, low, high); // 基准元素的正确位置
        // 对基准左边和右边的部分分别递归进行排序
        quickSort(arr, low, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, high);
    }
}
性能分析

时间复杂度：

平均情况下，快速排序的时间复杂度是 O(n log n)，其中 n 是待排序元素的数量。

在最坏情况下（数组已经有序或接近有序），快速排序的时间复杂度可能退化到 O(n^2)。

空间复杂度：

快速排序的空间复杂度主要取决于递归调用的栈空间，通常为 O(log n)。

在最坏情况下，递归栈的深度可能达到 n，空间复杂度为 O(n)。

稳定性：
快速排序是不稳定的排序算法，因为在分区过程中可能改变相同元素的相对顺序。

七，堆排序（Heap Sort）

原理

堆排序（Heap Sort）是一种基于二叉堆的排序算法。它将待排序数组构建成一个二叉堆，然后不断从堆顶取出最大（或最小）元素，将其放置到已排序部分的末尾，直到整个数组有序。

算法步骤

构建最大堆：将待排序数组看作完全二叉树，从最后一个非叶子节点开始，逐步向上调整，使得每个节点都大于其子节点。

不断从堆顶取出最大元素：每次将堆顶元素与堆末尾元素交换，然后将堆的大小减一，再进行堆化操作，将最大元素移至正确位置。

重复步骤 2，直到堆中只剩一个元素，此时整个数组有序。

算法实现
#include <iostream>
#include <vector>

// 交换元素
void swap(int& a, int& b) {
    a = a + b;
    b = a - b;
    a = a - b;
}

// 对以 root 为根的子树进行堆化
void heapify(std::vector<int>& arr, int n, int root) {
    int largest = root; // 初始化最大元素为根节点
    
    while (largest < n) {
        int left = 2 * root + 1; // 左子节点索引
        int right = 2 * root + 2; // 右子节点索引
        
        // 找到左右子节点中较大的元素索引
        if (left < n && arr[left] > arr[largest]) {
            largest = left;
        }
        if (right < n && arr[right] > arr[largest]) {
            largest = right;
        }
        
        // 如果最大元素不是根节点，则交换元素
        if (largest != root) {
            swap(arr[root], arr[largest]);
            root = largest; // 继续向下调整
        } else {
            break; // 堆结构已经满足，退出循环
        }
    }
}

// 堆排序
void heapSort(std::vector<int>& arr) {
    int n = arr.size();
    
    // 构建大根堆，从最后一个非叶子节点开始
    for (int i = n / 2 - 1; i >= 0; --i) {
        heapify(arr, n, i);
    }
    
    // 逐步取出最大元素并进行堆化
    for (int i = n - 1; i > 0; --i) {
        swap(arr[0], arr[i]); // 将堆顶元素移至已排序部分的末尾
        heapify(arr, i, 0); // 对剩余的部分进行堆化
    }
}
性能分析

时间复杂度：
堆排序的时间复杂度在最好、最坏和平均情况下都是 O(n log n)，其中 n 是待排序元素的数量。

空间复杂度：
堆排序的空间复杂度为 O(1)，只需要常数级别的额外空间。

稳定性：
堆排序通常是不稳定的，因为堆化操作可能改变相同元素的相对顺序。然而，通过一些额外的操作可以实现稳定性。

八，基数排序（Counting Sort）

原理

基数排序（Radix Sort）是一种非比较的整数排序算法，它根据数字的每个位上的值来对元素进行排序。基数排序可以看作是桶排序的扩展，它先按照最低位进行排序，然后逐步移到更高位，直到所有位都考虑完毕。

算法步骤

找到最大数的位数：首先，找到待排序数组中最大数的位数，这将决定排序的轮数。

按位排序：从低位到高位，依次对每一位进行计数排序（或桶排序），将元素分配到不同的桶中。

合并桶：将每一轮排序后的桶中的元素按顺序合并成一个新的数组。

重复步骤 2 和 3，直到所有位都考虑完毕，得到有序数组。

算法实现
#include <iostream>
#include <vector>
#include <queue>

// 找到数组中的最大数
int findMax(std::vector<int>& arr) {
    int max = arr[0];
    for (int num : arr) {
        if (num > max) {
            max = num;
        }
    }
    return max;
}

// 基数排序
void radixSort(std::vector<int>& arr) {
    int n = arr.size();
    int max = findMax(arr);
    int exp = 1; // 用于获取每个位数的值

    while (max / exp > 0) {
        // 创建桶队列，每个桶用于存放某个位数上的元素
        std::vector<std::queue<int>> buckets(10);   // 使用10个桶，每个桶代表一个数字（0到9）

        // 将元素分配到桶中
        for (int i = 0; i < n; ++i) {
            int bucketIndex = (arr[i] / exp) % 10; // 计算当前位数的值，作为桶的索引
            buckets[bucketIndex].push(arr[i]); // 将元素放入对应的桶中
        }

        // 从桶中取回元素到原数组
        int index = 0;
        for (int i = 0; i < 10; ++i) {
            while (!buckets[i].empty()) {
                arr[index++] = buckets[i].front(); // 取出队列头部元素，放入原数组
                buckets[i].pop(); // 弹出队列头部元素
            }
        }

        exp *= 10; // 移到下一个位数
    }
}
性能分析文章来源地址https://www.toymoban.com/news/detail-681249.html

时间复杂度：
基数排序的时间复杂度取决于位数和基数的大小。对于位数为 k，基数为 r 的情况，时间复杂度为 O(k * (n + r))。

空间复杂度：
基数排序的空间复杂度为 O(n + r)，其中 n 是待排序元素的数量，r 是基数的大小。

稳定性：
基数排序是稳定的排序算法，因为在同一位数上的排序时，相同值元素的相对顺序不会改变。