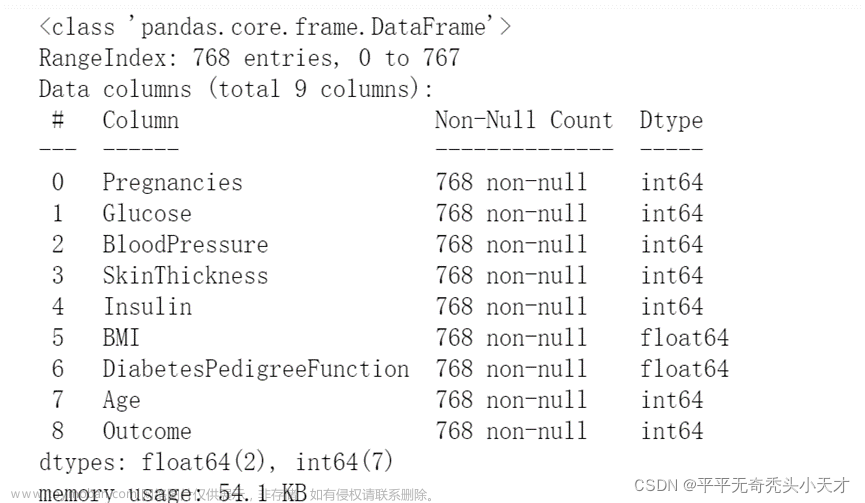
01
泊松回归

泊松回归(Poisson Regression)是一种广义线性模型,用于建立离散型响应变量(计数数据)与一个或多个预测变量之间的关系。它以法国数学家西蒙·丹尼·泊松(Siméon Denis Poisson)的名字命名,适用于计算“事件发生次数”的概率,比如交通事故发生次数、产品缺陷数量等离散计数数据。
泊松回归假设响应变量(因变量)Y服从泊松分布,该分布用于描述在固定时间或空间范围内发生事件的数量。泊松分布的特点是对于一个特定时间或空间区间,事件发生的平均速率是常数,并且事件之间是独立的。
泊松回归的模型形式如下:
log(λ) = β0 + β1*x1 + β2*x2 + ... + βn*xn其中,λ表示事件发生的平均速率(事件发生次数的期望),log是自然对数,β0, β1, β2, ..., βn是回归系数,x1, x2, ..., xn是预测变量。文章来源:https://www.toymoban.com/news/detail-681577.html
在泊松回归中,使用最大似然估计方法来估计回归系数,最大化观测数据在模型下的似然函数。泊松回归的结果表明每个预测变量对于事件发生次数的影响程度,系数的正负号表示预测变量与事件发生次数之间的正向或负向文章来源地址https://www.toymoban.com/news/detail-681577.html
到了这里,关于泊松回归和地理加权泊松回归的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!