浙大数据结构之09-排序1 排序-Toy模板网

这篇具有很好参考价值的文章主要介绍了浙大数据结构之09-排序1 排序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目详情：

给定N个（长整型范围内的）整数，要求输出从小到大排序后的结果。

本题旨在测试各种不同的排序算法在各种数据情况下的表现。各组测试数据特点如下：

数据1：只有1个元素；
数据2：11个不相同的整数，测试基本正确性；
数据3：103个随机整数；
数据4：104个随机整数；
数据5：105个随机整数；
数据6：105个顺序整数；
数据7：105个逆序整数；
数据8：105个基本有序的整数；
数据9：105个随机正整数，每个数字不超过1000。
输入格式:

输入第一行给出正整数N（≤105），随后一行给出N个（长整型范围内的）整数，其间以空格分隔。

输出格式:

在一行中输出从小到大排序后的结果，数字间以1个空格分隔，行末不得有多余空格。

输入样例:
```
11
4 981 10 -17 0 -20 29 50 8 43 -5
```
输出样例:
```
-20 -17 -5 0 4 8 10 29 43 50 981
```

主要思路：

把所有提到的排序都尝试复现一遍（才发现自己啥也不会）

（一）选择排序：

（1）简单选择排序：

在未排序序列中选出最小元素和序列首位元素交换，剩下来的序列以此类推

#include <stdio.h>
#include <stdlib.h>
#define MAX_NUM 100005
int Data[MAX_NUM];
void Swap(int* data1, int* data2) {
    int temp = *data1;
    *data1 = *data2;
    *data2 = temp;
    return;
}
void SimpleSelectionSort(int num, int data[]) {
    int minIndex;
    for(int i = 0; i < num - 1; i++) {
        minIndex = i;
        for(int j = i + 1; j < num; j++) {
           if(data[j] < data[minIndex]) {
               minIndex = j;
           } 
        }
        Swap(&data[i], &data[minIndex]);
    }
    return;
}
int main() {
    int num;
    scanf("%d", &num);
    for(int i = 0; i < num; i++) {
        scanf("%d", &Data[i]);
    }
    SimpleSelectionSort(num, Data);
    for(int i = 0; i < num; i++) {
        printf("%d", Data[i]);
        if(i != num - 1) printf(" ");
    }
    return 0;
}

（2）堆排序

首先将一个无序的序列生成最大堆，从树的倒数第二排最右边开始，下标是节点总数/2-1，然后依次递减1，不断将以当前下标为根节点的子树调整为最大堆

调整过程为下滤

接着不需要将堆顶元素输出，而是将堆顶元素与当前堆的最后一个元素交换位置，交换完位置后再将大小减1的堆重新调整成最大堆，重复上述过程，原来保存最大堆的数组就转换为一个从小到大的序列

/*堆排序建立堆的时候，
相对于之前建立堆是插入，
这个是在一堆无序的数字上建立
*/
#include <stdio.h>
#include <stdlib.h>
#define MAX_NUM 100005
int Data[MAX_NUM];
void Swap(int* a, int* b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
    return;
}
void PercDown(int data[], int root, int num) { //建立最大堆和从最大堆中弹出最大值，核心部分都是下滤
    //相对与之前的最大堆算法，本题特殊之处在于用于存储最大堆的数组不是从下标1开始，0做哨兵，而就是从0开始
    int parent, child;
    
    int tmp = data[root];
    //从root开始，遍历数组，比较当前值和左右子节点，若当前值大于左右子节点，则交换当前值和左右子节点的值，并重新调整最大堆
    for(parent = root; parent * 2 + 1 < num; parent = child) {
        child = parent * 2 + 1;
        if((child!= num - 1) && (data[child] < data[child + 1])) {
            child++;
        }
        if(tmp >= data[child]) {
            break;
        }
        else {
            data[parent] = data[child];
        }
    }
    data[parent] = tmp;
    return;
}
void HeapSort(int data[], int num) {
    //建立最大堆
    for(int i = num / 2 - 1; i >= 0; i--) {
        PercDown(data, i, num);
    }
    //删除最大堆顶
    for(int i = num - 1; i > 0; i--) {
        Swap(&data[0], &data[i]);
        PercDown(data, 0, i);
    }
}
int main() {
    int num;
    scanf("%d", &num);
    for(int i = 0; i < num; i++) {
        scanf("%d", &Data[i]);
    }
    HeapSort(Data, num);
    for(int i = 0; i < num; i++) {
        printf("%d", Data[i]);
        if(i != num - 1) {
            printf(" ");
        }
    }
    return 0;
}

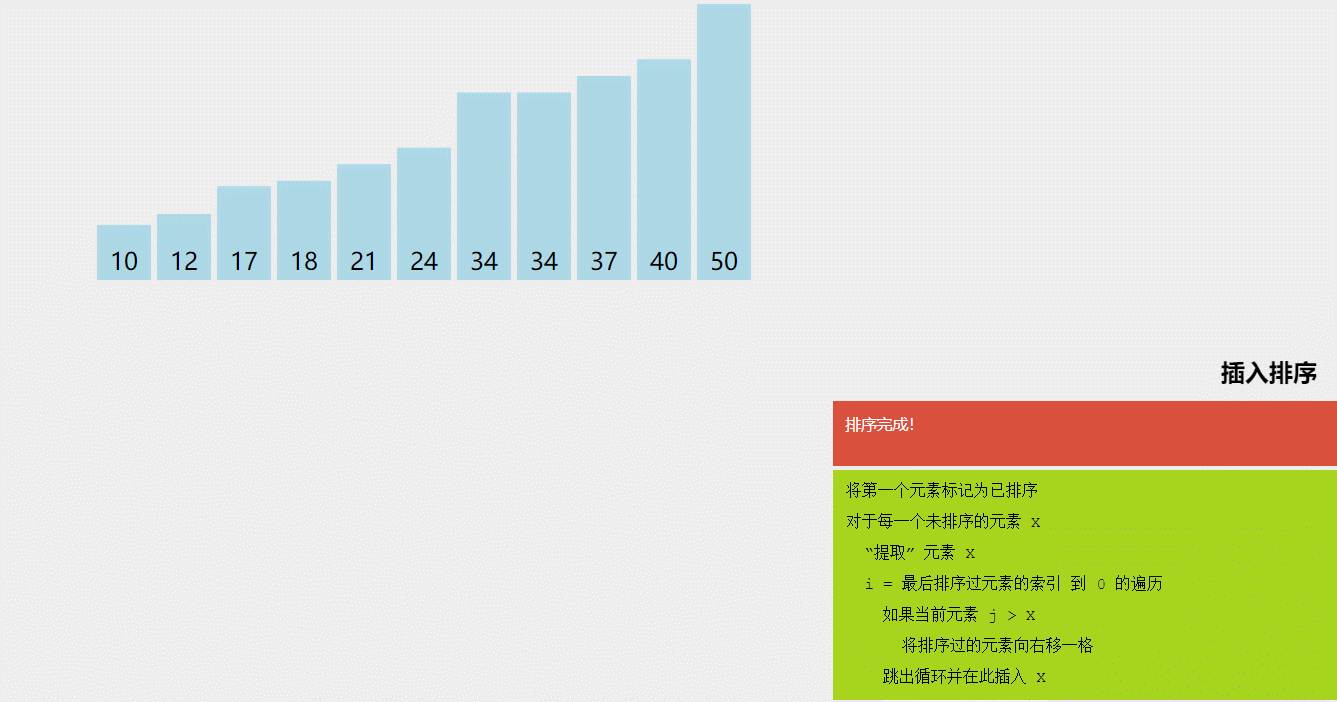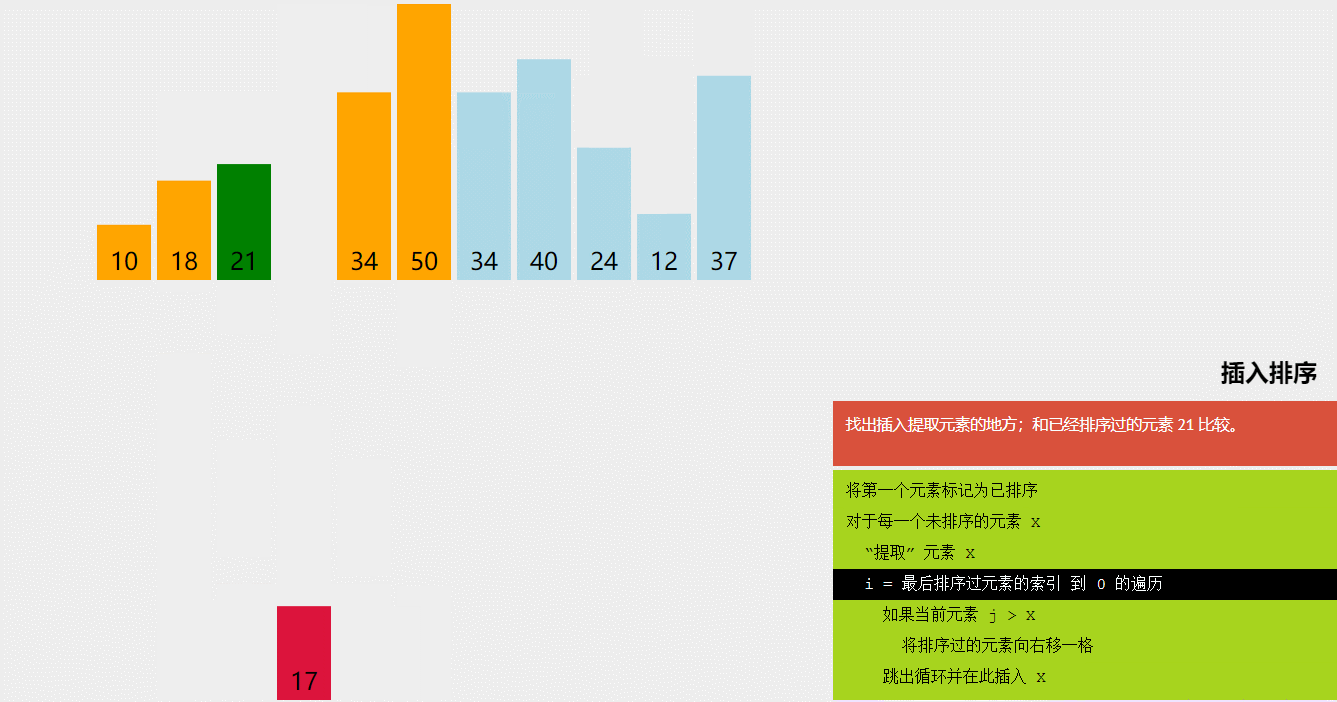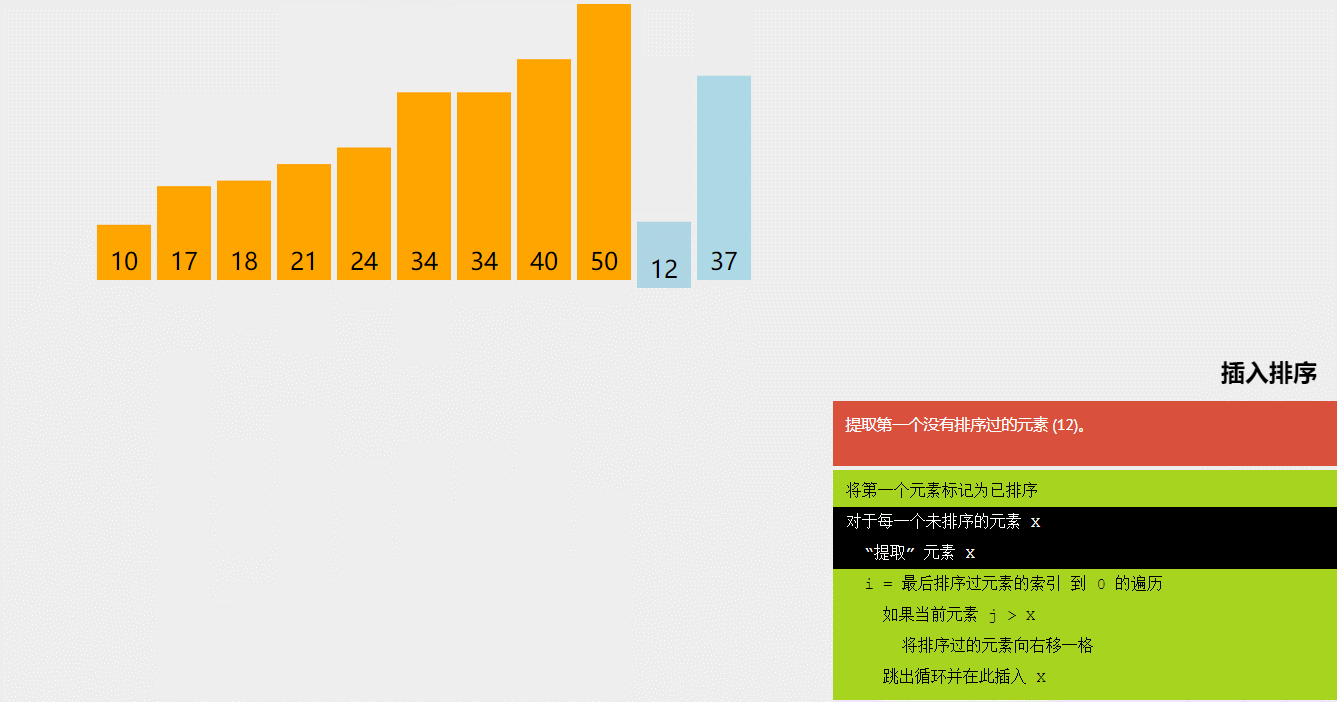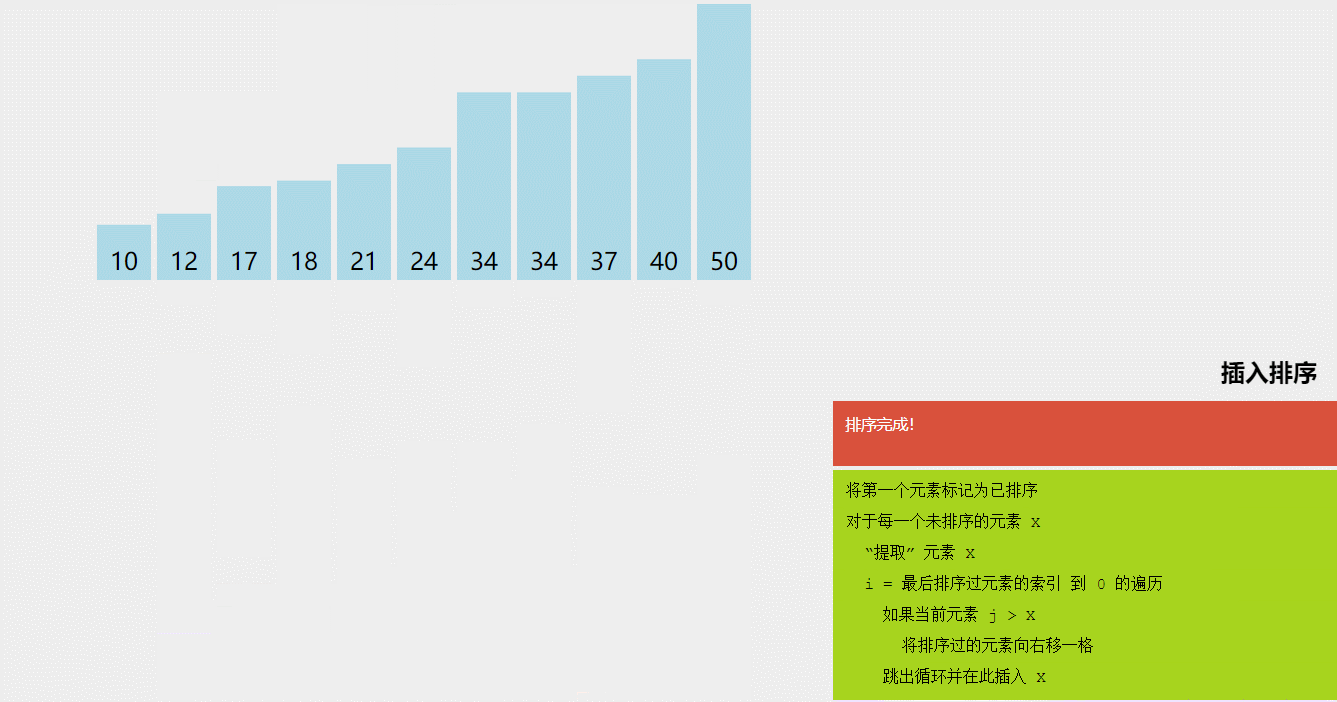
（二）插入排序

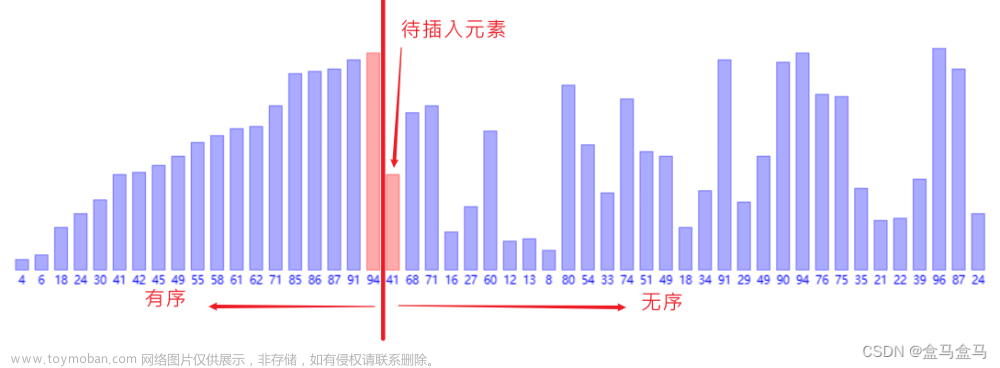
（1）简单插入排序

将序列分为已排和未排，每次从未排中取一个与已排比较直到合适位置后插入，重复上述过程，直到没有未排序列

#include <stdio.h>
#include <stdlib.h>
#define MAX_NUM 100005
int Data[MAX_NUM];
void SimpleInsertSort(int data[], int num) {
    for(int i = 1; i < num; i++) {
        int tmp = data[i];  //取出未排序列中第一个元素
        int j = i;
        for(; j > 0 && data[j - 1] > tmp; j--) {    //依次与已排序列从末尾往前比
            data[j] = data[j - 1];  
        }
        data[j] = tmp;  //将未排序列第一个元素插入到已排序列合适位置
    }
    return;
}
int main() {
    int num;
    scanf("%d", &num);
    for(int i = 0; i < num; i++) {
        scanf("%d", &Data[i]);
    }
    SimpleInsertSort(Data, num);
    for(int i = 0; i < num; i++) {
        printf("%d", Data[i]);
        if(i != num - 1) {
            printf(" ");
        }
    }
    return 0;
}

（2）希尔排序

通过将待排序的一组元素按一定间隔分为若干个序列，分别进行插入排序；最终间隔是1

往往用Sedgewick作为增量序列

void ShellSort(int data[], int num) {
    //定义一个增量数组
    int i;
    int sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0};

    //在sedgewick序列中找到比num小的增量，因为初始的增量sedgewick[i]不能超过待排序列长度
    for(i = 0; sedgewick[i] >= num; i++)    //在sedgewick序列中找到比num小的增量，因为初始的增量sedgewick[i]不能超过待排序列长度
        ;

    for(int interval = sedgewick[i]; interval > 0; interval = sedgewick[++i]) {
        //插入排序
       //比较难以理解，首先从一个intervel以后开始选择，因为下标0~intervel-1是分别intervel的第一个（第一个又是已排序列）
        for(int j = interval; j < num; j++) {  
            int tmp = data[j];  //取出未排序列中第一个元素
            int k = j;
            //依次将其已排序元素进行比较
            for(; k >= interval && data[k - interval] > tmp; k -= interval) {   //依次与已排序列从末尾往前比
                data[k] = data[k - interval];
            }
            data[k] = tmp;  //将未排序列的第一个元素插入到已排序列中合适位置
        }
    }
}

（三）交换排序

（1）冒泡排序

外层循环从待排序列最后一位往前依次确定，内层循环从前往后扫描两两比较取最大

减少循环的一个方法是每层循环设置一个flag，如果从头至尾扫描循环都没有交换，说明当前序列已经有序，可以break了

#include <stdio.h>
#define MAX_NUM 100005
#define bool int
#define TRUE 1
#define FALSE 0
int Data[MAX_NUM];
void Swap(int* a, int* b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
    return;
}
void BubbleSort(int data[], int num) {
    for(int i = num - 1; i >= 0; i--) {    //依次从下标num - 1开始往前定位
        bool flag = FALSE;  //标记该次循环中是否发生交换，若无，说明该序列已经有序
        for(int j = 0; j < i; j++) {
            if(data[j] > data[j + 1]) {
                Swap(&data[j], &data[j + 1]);
                flag = TRUE;
            }
        }
        if(flag == FALSE) {
            break;
        }
    }
    return;
}
int main() {
    int num;
    scanf("%d", &num);
    for(int i = 0; i < num; i++) {
        scanf("%d", &Data[i]);
    }
    BubbleSort(Data, num);
    for(int i = 0; i < num; i++) {
        printf("%d", Data[i]);
        if(i != num - 1) {
            printf(" ");
        }
    }
    return 0;
}

（2）快速排序

快速排序的思路是通过分治法，首先取一个pivot基准值，将大于pivot的都移到右边，小于它的都移到左边，将一个序列分成两个序列，然后将这两个序列分别重复上述操作

具体实现：

首先为了减少时间复杂度，要考究选择的pivot，方法是将最左边，最右边和中间（left + right)/2按最左边<=中间<=最右边，因为这样排序后最左边必定比中间小，最右边必定比中间大，将中间的值移动到最右边倒数第二个后，比较范围只用从最左边下标+1到最右边下标-2

另一个优化是因为递归针对较大数据还好，但对于较小数据就很慢，所以临设一个cutoff变量，当前序列大小比这个大就用快排，如果小就直接用简单插入排序

但发现这个cutoff最小必须设为2，再小就报错了，目前还没想出来是为什么

#include <stdio.h>
#define TRUE 1
#define FALSE 0
#define MAX_NUM 100005
typedef int bool;
int Data[MAX_NUM];
int Cutoff = 3;
void Swap(int* a, int* b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
    return;
}
/*实现简单插入排序*/
void SimpleInsertSort(int data[], int left, int right) {
    for(int i = left + 1; i <= right; i++) {
        int tmp = data[i];
        int j = i;
        for(; j > left && data[j - 1] > tmp; j--) {
            data[j] = data[j - 1];
        }
        data[j] = tmp;
    }
    return;
}
/*下面函数作用是确定快排中主元，将最左边、最右边、中间元素调整为
最左边 <= 中间 <= 最右边，此时最左边一定小于中间，最右边一定大于等于中间，这两个所以就不用考虑了
将中间的主元放到右边倒数第二个位置，下面就只用比较左边第二个到右边倒数第三个位置的范围就行*/
int CompareThreeNums(int data[], int left, int right) {
    int mid = (left + right) / 2;
    int max = data[left];
    if(data[left] > data[mid]) {
        Swap(&data[left], &data[mid]);
    }
    if(data[left] > data[right]) {
        Swap(&data[left], &data[right]);
    }
    if(data[mid] > data[right]) {
        Swap(&data[mid], &data[right]);
    }
    Swap(&data[mid], &data[right - 1]);
    return data[right - 1];
}
void QuickSortCore(int data[], int left, int right) {
    if(Cutoff <= right - left) {
        int pivot = CompareThreeNums(data, left, right);
        int low = left;
        int high = right - 1;
        while(TRUE) {
                while(data[++low] < pivot) ;
                while(data[--high] > pivot) ;
                if(low < high) {
                    Swap(&data[low], &data[high]);
                }
                else {
                    break;
                }
        }
        Swap(&data[low], &data[right - 1]); //将基准换到正确位置
        QuickSortCore(data, left, low - 1); //对基准左边序列递归
        QuickSortCore(data, low + 1, right);    //对基准右边序列递归
    }
    else {
        SimpleInsertSort(data, left, right); //对序列进行简单插入排序
    }
    return;
}
void QuickSort(int data[], int num) {
    QuickSortCore(data, 0, num - 1);
    return;
}
int main() {
    int num;
    scanf("%d", &num);
    for(int i = 0; i < num; i++) {
        scanf("%d", &Data[i]);
    }
    QuickSort(Data, num);
    for(int i = 0; i < num; i++) {
        printf("%d", Data[i]);
        if(i != num - 1) {
            printf(" ");
        }
    }
    return 0;
}

（四）归并排序

归并排序的思路类似于快排，不过归并是通过将待排序列不断分割到每个序列只剩两个数字时排序，然后再两两合并实现排序文章来源地址https://www.toymoban.com/news/detail-682057.html

①递归版本

#include <stdio.h>
#include <stdlib.h>
#define MAX_NUM 100005
int DataToSort[MAX_NUM];
void Merge(int data[], int tmpData[], int leftStart, int rightEnd, int rightStart) {
    int leftEnd = rightStart - 1;
    int tmpStart = leftStart;
    int num = rightEnd - leftStart + 1;
    while(leftStart <= leftEnd && rightStart <= rightEnd) {
        if(data[leftStart] <= data[rightStart]) {
            tmpData[tmpStart++] = data[leftStart++];
        }
        else {
            tmpData[tmpStart++] = data[rightStart++];
        }
    }    
    while(leftStart <= leftEnd) {
        tmpData[tmpStart++] = data[leftStart++];
    }
    while(rightStart <= rightEnd) {
        tmpData[tmpStart++] = data[rightStart++];
    }
    for(int i = 0; i < num; i++, rightEnd--) {
        data[rightEnd] = tmpData[rightEnd];
    }
    return;
}
void MergeSortRecursiveVersionCore(int data[], int tmpData[],int leftStart, int rightEnd) {
    if(leftStart >= rightEnd) {
        return;
    }
    int mid = (leftStart + rightEnd) / 2;
    MergeSortRecursiveVersionCore(data, tmpData, leftStart, mid);
    MergeSortRecursiveVersionCore(data, tmpData, mid + 1, rightEnd);
    Merge(data, tmpData, leftStart, rightEnd, mid + 1);
    return;
}
void MergeSort(int data[], int num) {
    int* tmpData = (int*)malloc(sizeof(int) * num);
    MergeSortRecursiveVersionCore(data, tmpData, 0, num - 1);
    free(tmpData);
    return;
}
int main() {
    int num;
    scanf("%d", &num);
    for(int i = 0; i < num; i++) {
        scanf("%d", &DataToSort[i]);
    }
    MergeSort(DataToSort, num);
    for(int i = 0; i < num; i++) {
        printf("%d", DataToSort[i]);
        if(i != num - 1) {
            printf(" ");
        }
    }
    return 0;
}

②循环版本

#include <stdio.h>
#include <stdlib.h>
#define MAX_NUM 100005
int DataToSort[MAX_NUM];
void Merge(int data[], int tmpData[], int leftStart, int rightStart, int rightEnd) {
    int leftEnd = rightStart - 1;
    int tmpStart = leftStart;
    int numElements = rightEnd - leftStart + 1;
    while(leftStart <= leftEnd && rightStart <= rightEnd) {
        if(data[leftStart] <= data[rightStart]) {
            tmpData[tmpStart++] = data[leftStart++];
        }
        else {
            tmpData[tmpStart++] = data[rightStart++];
        }
    }
    while(leftStart <= leftEnd) {
        tmpData[tmpStart++] = data[leftStart++];
    }
    while(rightStart <= rightEnd) {
        tmpData[tmpStart++] = data[rightStart++];
    }
    for(int i = 0; i < numElements; i++, rightEnd--) {
        data[rightEnd] = tmpData[rightEnd];
    }
    return;
}
/*length表示当前有序序列*/
void MergeCirculationSortCore(int data[], int tmpData[], int length, int totalNum) {
    /*i表示当前序列中左开头*/
    /*下面代码中传i， i + length, i + 2 * length - 1等都是坐标*/
    int i;
    for(i = 0; i <= totalNum - 2 * length; i += 2 * length) {    
        Merge(data, tmpData, i, i + length, i + 2 * length - 1);
    }
    /*如果剩余的序列已经小于等于两个length但依然比一个length长*/
    if(i + length < totalNum) {
        Merge(data, tmpData, i, i + length, totalNum - 1);
    }
    /*如果剩余的序列已经不足一个length*/
    else {
        for(int j = i; j < totalNum; j++) {
            tmpData[j] = data[j];
        }
    }
    return;
}
void MergeCirculationSort(int data[], int num) {
    int length = 1;
    while(length < num) {
        int* tmpData = (int*)malloc(sizeof(int) * num);
        /*第一次先对按length长度的序列排序*/
        MergeCirculationSortCore(DataToSort, tmpData, length, num);
        length *= 2;
        /*第二次对之前length长度的2倍的序列归*/
        MergeCirculationSortCore(tmpData, data, length, num);
        length *= 2;    
        free(tmpData);    
    }
    return;
}
int main() {
    int num;
    scanf("%d", &num);
    for(int i = 0; i < num; i++) {
        scanf("%d", &DataToSort[i]);
    }
    MergeCirculationSort(DataToSort, num);
    for(int i = 0; i < num; i++) {
        printf("%d", DataToSort[i]);
        if(i != num - 1) {
            printf(" ");
        }
    }   
    return 0;
}

到了这里，关于浙大数据结构之09-排序1 排序的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！