栈：后进先出的数据结构-Toy模板网

这篇具有很好参考价值的文章主要介绍了栈：后进先出的数据结构。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

栈与队列

在计算机科学中，栈（Stack）是一种常见的数据结构，它的特殊性在于遵循后进先出（Last-In-First-Out，LIFO）的原则。栈被广泛应用于各种计算机算法和程序设计中，它的简单而有效的特性使得它在解决许多问题时都能发挥重要作用。

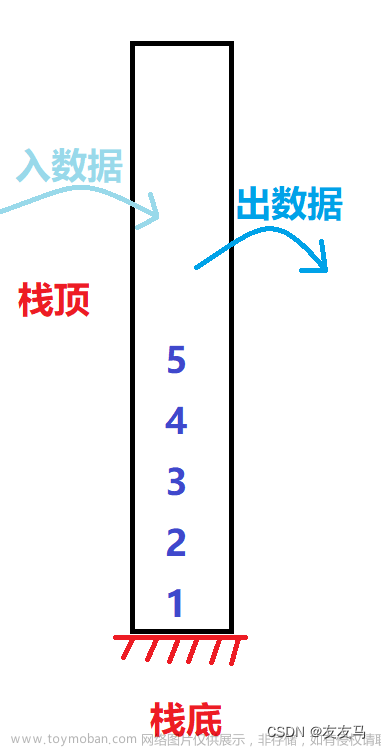
栈的工作原理

栈的工作原理可以类比成一个物理上的堆叠，就像一叠盘子。最先放入的盘子位于底部，最后放入的盘子位于顶部，而取盘子的时候总是从顶部开始取。这种特性决定了栈的后进先出的行为。具体来说，栈支持以下两个基本操作：

入栈（Push）
将元素放入栈的顶部。新元素会成为栈顶，而原来的栈顶元素会下移一个位置。
出栈（Pop）
从栈的顶部取出栈顶元素。取出后，栈顶下移一个位置。

这里笔者用字符画生动的做了一个图来供大家理解原理

初始状态:   栈为空

入栈操作:
1. 将元素A入栈
   栈顶
   ------
   |  A |
   ------

2. 将元素B入栈
   栈顶
   ------
   |  B |
   ------
   |  A |
   ------

3. 将元素C入栈
   栈顶
   ------
   |  C |
   ------
   |  B |
   ------
   |  A |
   ------

出栈操作:
1. 执行出栈操作
   栈顶
   ------
   |  B |
   ------
   |  A |
   ------

2. 再次执行出栈操作
   栈顶
   ------
   |  A |
   ------

3. 执行出栈操作后，栈为空
   栈为空

栈还通常提供一个**查看栈顶（Peek）**的操作，用于查询当前栈顶的元素而不将其移出栈。

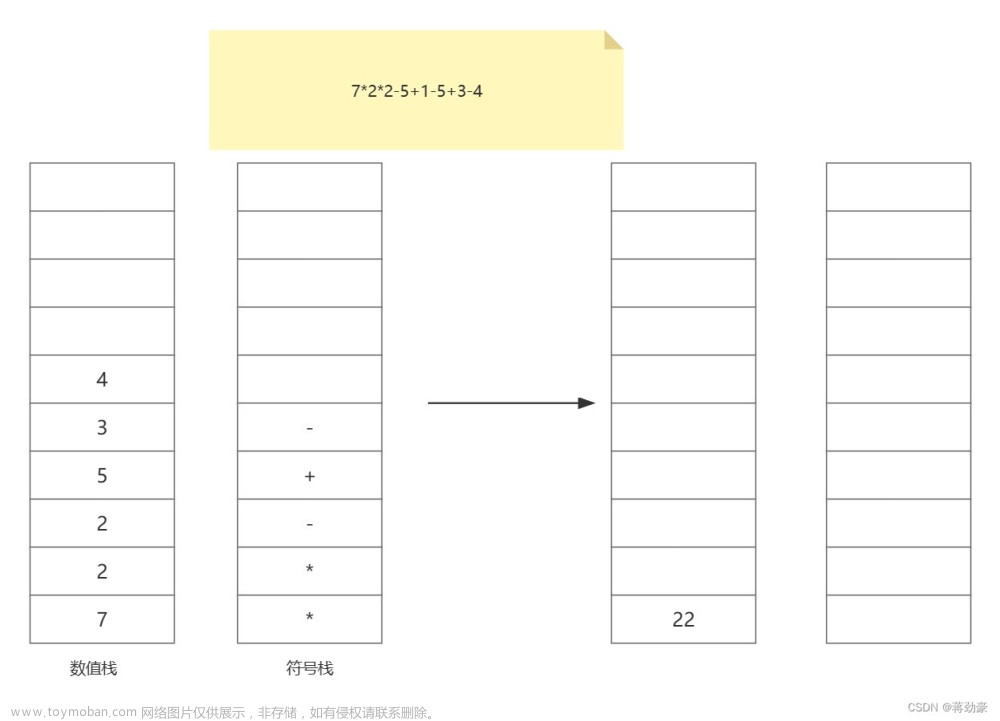
栈的应用示例：表达式求值

考虑一个实际应用的例子：数学表达式的求值。我们要解析一个数学表达式并计算其结果。这里我们以中缀表达式为例，中缀表达式是我们通常使用的数学表达式，例如 "3 + 5 * ( 2 - 8 )". 我们可以通过栈来实现表达式的求值。

操作数栈（Operand Stack）
我们使用一个栈来存储操作数，即数字。当解析到一个数字时，将其入栈。
运算符栈（Operator Stack）
我们使用另一个栈来存储运算符。当解析到一个运算符时，需要根据运算符的优先级和结合性来判断是否需要进行计算。

例如，考虑表达式 "3 + 5 * ( 2 - 8 )"：

遇到 "3"，将其入操作数栈。
遇到 "+"，由于运算符栈为空，直接入栈。
遇到 "5"，将其入操作数栈。
遇到 ""，由于 "" 的优先级高于 "+"，将其入运算符栈。
遇到 "("，将其入运算符栈。
遇到 "2"，将其入操作数栈。
遇到 "-"，由于 "-" 的优先级低于 ""，弹出 "" 运算符并进行计算，结果入操作数栈。
遇到 "8"，将其入操作数栈。
遇到 ")"，弹出运算符栈中的 "("，弹出 "*" 运算符并进行计算，结果入操作数栈。
弹出运算符栈中的 "+" 运算符并进行计算，得到最终结果。

通过使用栈，我们可以按照正确的顺序解析表达式并计算出结果。

浏览器进退（使用栈）

想象你正在使用一个浏览器浏览网页，每当你访问一个新的网页时，浏览器会将该网页的信息存储在一个栈中，表示你的浏览历史。如果你想后退，浏览器会从栈中弹出当前网页，然后显示前一个网页。如果你想前进，浏览器可以从另一个栈中弹出被后退时移出的网页，然后显示它。下面笔者用一个C++代码来实现这个功能

#include <iostream>
#include <stack>
#include <string>

class Browser {
private:
    std::stack<std::string> backStack;  // 后退栈
    std::stack<std::string> forwardStack;  // 前进栈
    std::string currentURL;  // 当前网页的URL

public:
    Browser() {
        currentURL = "about:blank";  // 默认打开空白页面
    }

    void visit(const std::string& url) {
        backStack.push(currentURL);
        currentURL = url;
        while (!forwardStack.empty()) {
            forwardStack.pop();  // 访问新页面后，前进栈被清空
        }
    }

    bool canGoBack() {
        return !backStack.empty();
    }

    bool canGoForward() {
        return !forwardStack.empty();
    }

    void goBack() {
        if (canGoBack()) {
            forwardStack.push(currentURL);
            currentURL = backStack.top();
            backStack.pop();
        }
    }

    void goForward() {
        if (canGoForward()) {
            backStack.push(currentURL);
            currentURL = forwardStack.top();
            forwardStack.pop();
        }
    }

    std::string getCurrentURL() {
        return currentURL;
    }
};

int main() {
    Browser browser;

    browser.visit("https://www.example.com");
    std::cout << "当前页面：" << browser.getCurrentURL() << std::endl;

    browser.visit("https://www.openai.com");
    std::cout << "当前页面：" << browser.getCurrentURL() << std::endl;

    if (browser.canGoBack()) {
        browser.goBack();
        std::cout << "后退后页面：" << browser.getCurrentURL() << std::endl;
    }

    if (browser.canGoForward()) {
        browser.goForward();
        std::cout << "前进后页面：" << browser.getCurrentURL() << std::endl;
    }

    return 0;
}