融合正余弦和柯西变异的麻雀搜索算法(Matlab代码实现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了融合正余弦和柯西变异的麻雀搜索算法(Matlab代码实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

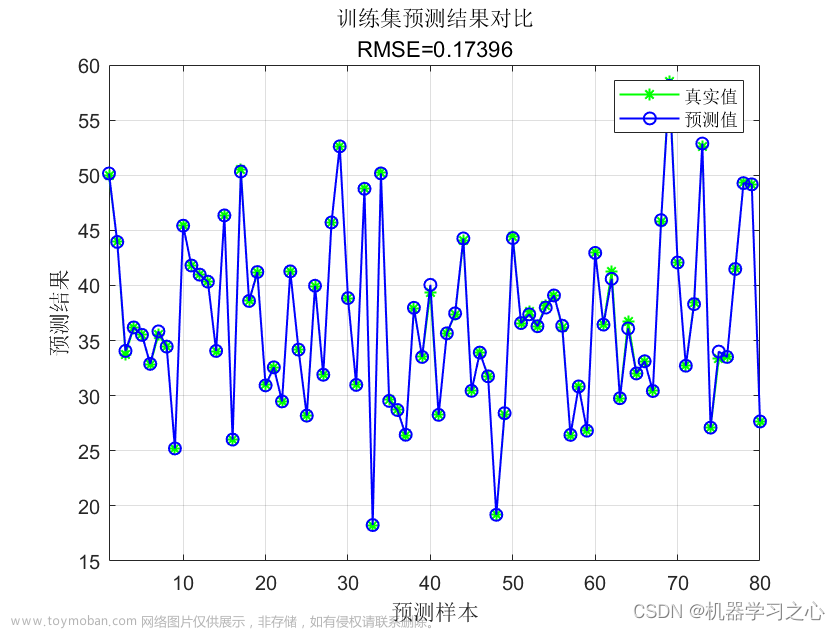
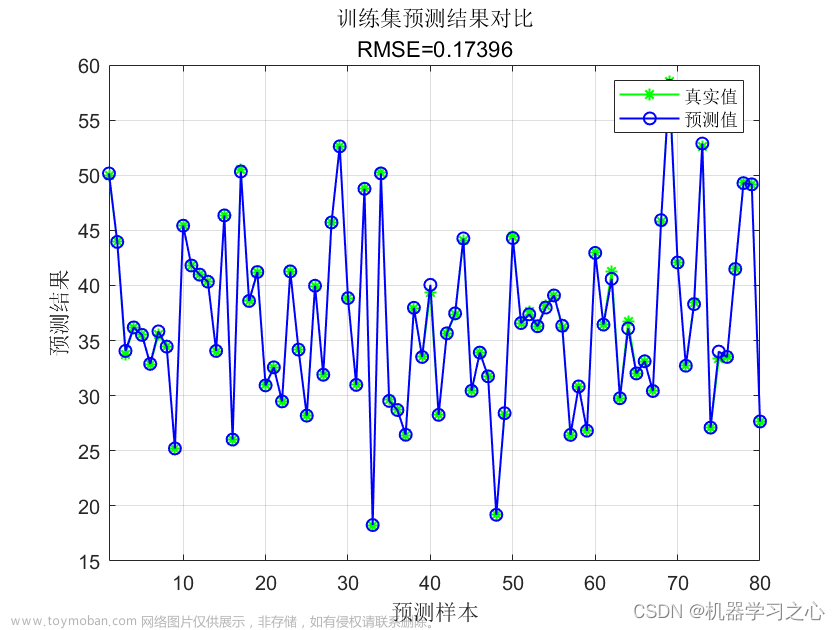
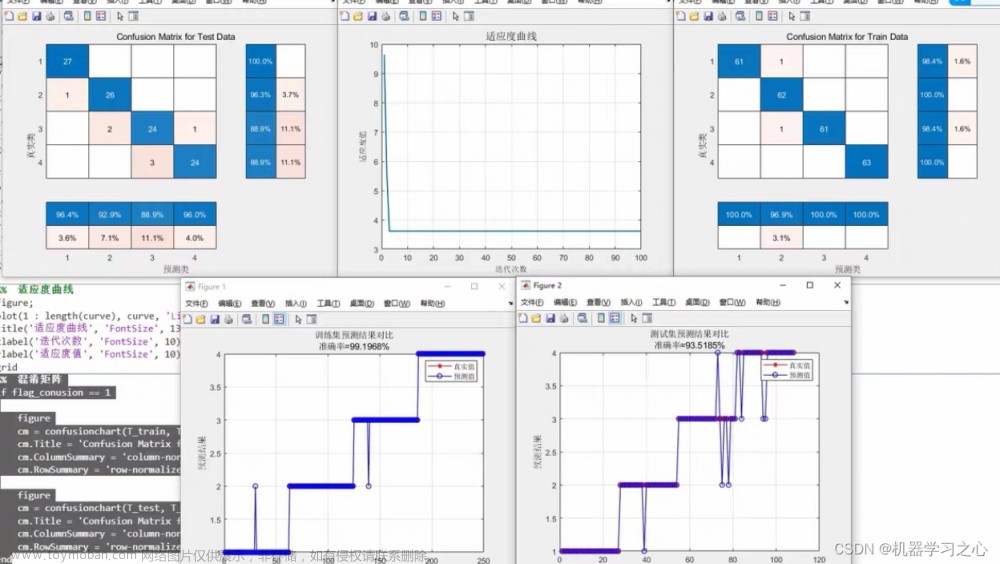
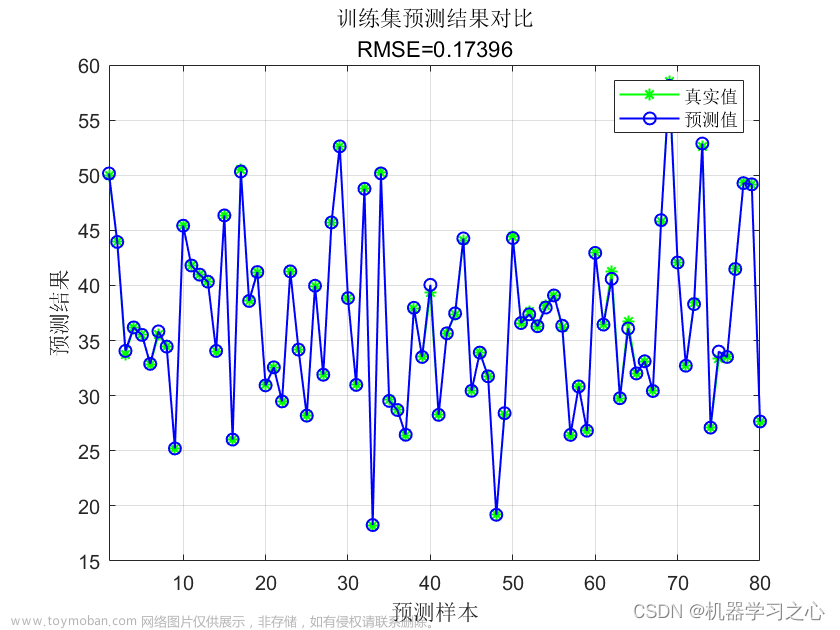
📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

麻雀搜索算法（sparrow search algorithm，SSA）是薛建凯等[1] 在2020年提出的一种新型优化算法，主要通过模拟麻雀捕食和反捕食的行为特征进行数学建模。麻雀搜索算法具备结构简单、控制参数少、求解精度高等优点。尽管出现时间较短，但在实际工程应用也逐步增加，Liu 等[2] 针对现有的脑瘤诊断算法存在成功率不足，以及在治疗过程中不能及时跟踪进程，引进了 SSA进行优化，增强了检测能力。Zhu 等[3] 使用 SSA 对聚合物电解质燃料电池（PEMFC）堆的辨识参数进行优化，成功地降低了电池中电压误差，提高了电能转换效率。

针对SSA算法在寻优后期出现群体多样性损失，造成落入局部极值的几率升高，引发收敛精度不足问题，本文采用一种折射反向学习机制对麻雀种群初始化。反向学习是 Tizhoosh 提出的一种优化策略[9] ，基本思想是通过计算当前解的反向解来扩大搜索范围，借此找出给定问题更好的备选解。文献[10-11]将智能算法与反向学习结合，均能有效提高算法求解精度。同时反向学习仍存在一定的不足，在寻优早期引进反向学习能够加强算法的收敛性能，但在后期易使算法陷入早熟收敛。

因此在反向学习策略中引进一种折射原理[12] 以降低算法在搜索后期陷入早熟收敛的几率。折射反向学习原理如图1所示。

融合正余弦和柯西变异的麻雀搜索算法(Matlab代码实现）,matlab,数学建模,开发语言

📚2 运行结果

融合正余弦和柯西变异的麻雀搜索算法(Matlab代码实现）,matlab,数学建模,开发语言

部分代码：

%% Figure
figure1 = figure('Color',[1 1 1]);
G1=subplot(1,2,1,'Parent',figure1);
func_plot(Function_name)
title(Function_name)
xlabel('x')
ylabel('y')
zlabel('z')
subplot(1,2,2)
G2=subplot(1,2,2,'Parent',figure1);
CNT=35;
k=round(linspace(1,iter,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:iter;
semilogy(iter(k),PSO_curve(k),'k-','linewidth',1);
hold on
semilogy(iter(k),GWO_Convergence_curve(k),'r-','linewidth',1);
hold on
semilogy(iter(k),SSA_Convergence_curve(k),'c-','linewidth',1);
hold on
semilogy(iter(k),SCSSA_Convergence_curve(k),'m-','linewidth',1);
grid on;
title('收敛曲线')
xlabel('迭代次数');
ylabel('适应度值');
box on
legend('PSO','GWO','SSA','SCSSA')
set (gcf,'position', [300,300,800,320])