二叉树的构建及遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树的构建及遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

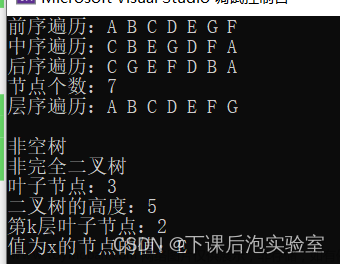
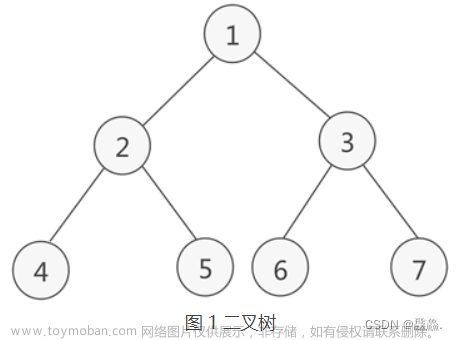
二叉树的构建及遍历

题目要求

二叉树的构建及遍历,刷题,笔记,c语言
题目链接

示例

解答

方法一、

先构建二叉树，再中序遍历。

实现思路

按照给出的字符串创建二叉树，先依次访问字符串中的字符，如果遇到不为’#'的字符，就将该结点的值赋值为该字符，然后再创建两个新结点，分别为该结点的左孩子和右孩子，然后递归调用方法，使左孩子和右孩子进行同样操作。如果遇到#字符，就将该结点堆顶值赋值为#,然后直接退出函数，即不再创建该结点的左右孩子结点。

时间复杂度和空间复杂度

代码

#include <stdio.h>
#include <stdlib.h>
typedef char BTDataType;
//定义二叉树的结点
typedef struct BinaryTreeNode
{
    BTDataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

void CreateBinaryTree(BTNode* root, char** arr)
{
    //如果**arr为'\0'，则说明字符串已经结束
    if (*(*arr) == '\0')
    {
        return;
    }
    //如果**arr不为#，就将该结点的值为**arr，同时让(*arr)++
    //此时arr里面存的还是*arr的地址，但是(*arr)++后，*arr中存的地址已经为字符串中下一个字符的地址。
    if (*(*arr) != '#')
    {
        root->data = *(*arr);
        (*arr)++;
    }
    //如果**arr为#,就将该结点的值为#,然后同样将*arr中存的地址向后移一位。
    else
    {
        root->data=*(*arr);
        (*arr)++;
        return;
    }
    //如果该结点不为空结点，就创建两个结点，来当作该结点的左右孩子。
    BTNode* left = (BTNode*)malloc(sizeof(BTNode));
    BTNode* right = (BTNode*)malloc(sizeof(BTNode));
    root->left = left;
    root->right = right;
    //然后递归使该结点的左右孩子完成上述同样操作。
    CreateBinaryTree(root->left, arr);
    CreateBinaryTree(root->right, arr);
}
void InOrder(BTNode* root)
{
    //如果root结点的值为#,就说明该结点为空结点，不需要打印，直接退出函数
    if (root->data=='#')
    {
        return;
    }
    //先遍历该结点的左子树
    InOrder(root->left);
    //然后再打印该节点的值
    printf("%c ", root->data);
    //然后再遍历该结点的右子树
    InOrder(root->right);
}
int main() {
    char arr[100] = { 0 };
    scanf("%s", arr);
    //创建二叉树的根节点
    BTNode* bt = (BTNode*)malloc(sizeof(BTNode));
    //将字符串中第一个字符的地址赋值给pa
    char* pa = &arr[0];
    //将指针pa的地址赋给ppa,即ppa为二级指针，通过*ppa就可以得到pa，即得到字符串中第一个字符的地址。
    //当*ppa+1时，即*ppa+1指向字符串的第二个字符的地址，所以可以通过*ppa++来访问字符串的每个字符
    char** ppa = &pa;
    //将二叉树根节点和ppa当作实参
    CreateBinaryTree(bt, ppa);
    InOrder(bt);
    return 0;
}

方法二、

比第一种方法更简洁易懂

实现思路

和第一种方法相似，都是先按照给出的先序遍历的顺序创建二叉树，然后进行中序遍历。文章来源地址https://www.toymoban.com/news/detail-683890.html

时间复杂度和空间复杂度

代码

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef char BTDataType;
//定义二叉树的结点
typedef struct BinaryTreeNode
{
    BTDataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

//创建一个二叉树结点并返回
BTNode* BuyBTNode(BTDataType x)
{
    BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
    newNode->data=x;
    newNode->left=NULL;
    newNode->right=NULL;
    return newNode;
}

BTNode* CreateBinaryTree(char* arr,int* count)
{
    //如果现在访问的字符为#,则说明该结点为NULL，让(*count)++，即访问下一个字符，然后返回NULL
    if(arr[*count]=='#')
    {
        (*count)++;
        return NULL;
    }
    //如果现在访问的字符不为#,将该字符存入到新创建的结点中，
    BTNode* root = BuyBTNode(arr[(*count)++]);
    //然后再将该结点的左孩子和右孩子递归调用该函数
    //如果该结点有左孩子，则会返回创建的新结点
    //如果该结点没有左孩子，则会返回NULL
    root->left = CreateBinaryTree(arr, count);
    root->right = CreateBinaryTree(arr, count);
    //然后将根结点返回
    return root;
}
void InOrder(BTNode* root)
{
    if(root==NULL)
    {
        return ;
    }
    InOrder(root->left);
    printf("%c ",root->data);
    InOrder(root->right);
}
int main()
{
    char arr[100]={0};
    scanf("%s",arr);
    int count = 0;
    //CreateBinaryTree函数会返回创建的二叉树的根节点
    BTNode* bt = CreateBinaryTree(arr, &count);
    InOrder(bt);
}