1 介绍
1.1 概述
概率论是与概率有关的数学分支。虽然有几种不同的概率解释,但概率论通过一组公理来表达该概念,以严格的数学方式对待该概念。通常,这些公理用概率空间形式化概率,将取值在 0 到 1 之间的度量(称为概率度量)分配给称为样本空间的一组结果。样本空间的任何指定子集称为事件。概率论的中心主题包括离散和连续随机变量、概率分布和随机过程(提供非确定性或不确定过程或测量量的数学抽象,这些量可能是单次出现的,也可能随时间以随机方式演变)。尽管不可能完美地预测随机事件,但关于它们的行为可以说很多。描述这种行为的概率论的两个主要成果是大数定律和中心极限定理。
作为统计学的数学基础,概率论对于许多涉及数据定量分析的人类活动至关重要。概率论方法也适用于仅给出部分状态知识的复杂系统的描述,如统计力学或序贯估计。二十世纪物理学的一个伟大发现是量子力学中描述的原子尺度物理现象的概率本质。
1.2 概率论发展历史
- 人类认识到随机现象的存在是很早的。 从太古时代起,估计各种可能性就一直是人类的一件要事。 早在古希腊哲学家就已经注意到必然性与偶然性问题; 我国春秋时期也已有可考词语(辞海)。
- 1494年,意大利数学家帕乔利(L. pacioli) 出版的《算术》一书中就有以下问题:两人进行赌博,规定谁先获胜 6 场谁为胜者。 一次 ,当甲已获胜 5 场 ,乙也获胜 2 场时,比赛因故中断。那么,赌注该如何分配呢?所给答案为将赌注分成 7 份,按 5 :2 分给甲乙两人。
- 1560年代,卡尔达诺在其著作《Liber de ludo aleae》中系统地研究了概率论,他将胜算定义为赢和输的结果次数之比。
- 1654年,帕斯卡 Pascal 和费马 Fermat 在互通书信时讨论了概率论,可以视作是概率论的开端。数学期望的概念在这次讨论中诞生。
- 1657 年,荷兰数学家惠更斯 Huygens,出版了《De ratiociniis in ludo aleae》(《论赌博中的计算》)一书。其到巴黎的时候,听说帕斯卡与费马在研究概率问题,便也参与进来。其书中给出了第一批概率论概念和定理(如加法定理、乘法定理)。
- 费马、帕斯卡和惠更斯,三人提出的解法中,都首先涉及了数学期望(mathematical expectation)这一概念,并由此奠定了古典概率的基础。
- 1710年代,瑞士数学家 伯努利 Bernoulli 发现了大数定律,并著有《Ars Conjectandi》(《猜度术》)。
- 1733年,法国数学家 棣莫弗 De Moivre 独立引进了正态分布。给出了中心极限定理的特殊形式,并编写了《The Doctrine of Chances》。
- 1777年,蒲丰(G.L.L Buffon) 提出了投针问题的几何概率;
- 1809年,德国数学家 高斯 Gauss 也独立引进了正态分布,创立了误差理论,特别地,创立了最小二乘的基本方法。
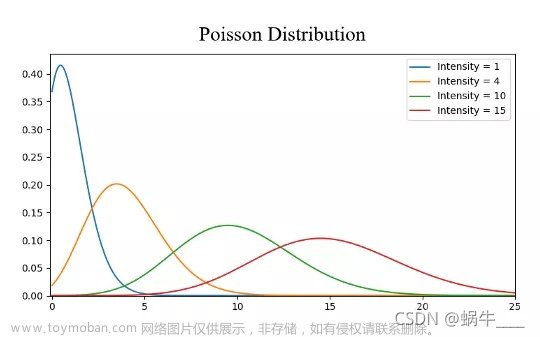
- 1837年,法国数学家 泊松陈述了泊松大数定律,其将伯努利大数定律做了推广,研究得出了一种新的分布,就是泊松分布。
- 1812年,法国数学家 拉普拉斯(P. S.Laplace ,1749 —1827) 出版的《概率的分析理论》以强有力的分析工具处理概率论的基本内容,使以往零散的结果系统化.。拉普拉斯的著作实现了从组合技巧向分析方法的过渡,开辟了概率论发展的新时期。该著作棣莫弗的成果由受到了关注。因此,棣莫弗-拉普拉斯定理以他们的名字命名。正是在这部著作中,拉普拉斯给出了概率的古典定义:
事件 A 的概率 P( A) 等于一次试验中有利于事件A的可能结果数与该试验中所有可能结果数之比。 - 1866年,俄国数学家切比雪夫 (п. л.чеъыщев,1821 —1894) 建立了关于独立随机变量序列的大数定律,使伯努利定理和泊松大数定理成为其特例。切比雪夫还将 棣莫弗–拉普拉斯 极限定理推广为更一般的中心极限定理。
- 切比雪夫的成果后又被他的学生马尔可夫 Markov( А. А. маркоъ,1856 —1922)发扬光大,推进了 20 世纪概率论发展的进程。马尔可夫对概率论的重大贡献之一是创立了概率论的一个分支:研究相依随机变量的理论,称为“马尔可夫过程”。为证明概率论的中心极限定理,Chebyshev 与 Markov 利用的是矩方法,而 Lyapunov 利用了特征函数方法。极限定理的后续发展表明特征函数方法是一种强大的解析工具。
- 1901年,概率论中心极限定理被严格的证明了,数学家们利用这一定理第一次科学地解释了为什么实际中遇到的许多随机变量近似服从以正态分布。
- 1902年,勒贝格在他论文中确立了测度论的基础。
- 1909年,博雷尔在勒贝格影响下,给出了无数次抛硬币的强大数定律。这一成果被豪斯道夫,哈代,李特尔伍德,Steinhaus等人进一步发展。在这些研究的基础上,辛钦给出了重对数律。
- 1933年,科尔莫戈罗夫 Kolmogorov 以德文出版了经典性著作著《Foundations of the Theory of Probability》(《概率论基础》)。从20 世纪20 年代中期起,科尔莫戈罗夫开始从测度论途径探讨整个概率论理论的严格表述。1926年,他推导了弱大数定律成立的主要条件,后又对博雷尔提出的强大数定律问题给出了一般的结果,推广了切比雪夫不等式,提出了科尔莫戈罗夫不等式,创立了可数集马尔可夫链理论。科尔莫戈罗夫是莫斯科函数论学派领导人鲁金 (н. н.Λузин,1883 —1950) 的学生,对实函数论的运用可以说是炉火纯青。他在这部著作中建立起集合测度与事件概率的类比、积分与数学期望的类比、函数正交性与随机变量独立性的类比 ……,等等。这种广泛的类比终于赋予了概率论以演绎数学的特征。科尔莫戈罗夫的公理系统逐渐获得了数学家们的普遍承认,由于公理化,概率论成为一门严格的演绎科学,取得了与其他数学分支同等的地位。




1.3 统计学发展历史
统计学发展的概貌,大致可划分为古典记录统计学、近代描述统计学和现代推断统计学三种形态。
- 1560年代,卡尔达诺在其著作《Liber de ludo aleae》中系统地研究了概率论,他将胜算定义为赢和输的结果次数之比。
- 1654年,帕斯卡 Pascal 和费马 Fermat 在互通书信时讨论了概率论,可以视作是概率论的开端。数学期望的概念在这次讨论中诞生。
- 1662年,英国统计学家J.格兰特组织调查伦敦的人口死亡率,并发表专著《从自然和政治方面观察死亡统计表》,格兰特还对保险统计、经济统计进行了数学研究,称其学问为“政治算术”。他发现人口出生率与死亡率相对稳定,提出了“大数恒静定律”,之后统计学的数学性质逐渐加重。
- 1710年代,瑞士数学家 伯努利 Bernoulli 发现了大数定律,并著有《Ars Conjectandi》(《猜度术》)。
- 1733年,法国数学家 棣莫弗 De Moivre 独立引进了正态分布。给出了中心极限定理的特殊形式,并编写了《The Doctrine of Chances》。
-
- 1763年,英国统计学家贝叶斯(T.Bayes)发表《论机会学说问题的求解》,给出“贝叶斯定理”,从结果去对原因进行后验概率的计算,可视为最早的数学化的统计推断。
- 1777年,蒲丰(G.L.L Buffon) 提出了投针问题的几何概率;
- 1809年,德国数学家 高斯 Gauss 也独立引进了正态分布,创立了误差理论,特别地,创立了最小二乘的基本方法。
- 1837年,法国数学家 泊松陈述了泊松大数定律,其将伯努利大数定律做了推广,研究得出了一种新的分布,就是泊松分布。
- 1812年,法国数学家 拉普拉斯(P. S.Laplace ,1749 —1827) 出版的《概率的分析理论》以强有力的分析工具处理概率论的基本内容,使以往零散的结果系统化.。拉普拉斯的著作实现了从组合技巧向分析方法的过渡,开辟了概率论发展的新时期。该著作棣莫弗的成果由受到了关注。因此,棣莫弗-拉普拉斯定理以他们的名字命名。正是在这部著作中,拉普拉斯给出了概率的古典定义:
事件 A 的概率 P( A) 等于一次试验中有利于事件A的可能结果数与该试验中所有可能结果数之比。 - 在19世纪末和20世纪初,英国统计学家卡尔·皮尔逊(Karl Pearson)提出方差和标准差的概念。卡尔·皮尔逊是现代统计学的创始人之一。并在1895年首次提出「偏态(skewness)」。
- 19世纪下半叶,俄罗斯的彼得堡学派引入「随机变量」。这标志着概率论由古典概率时期进入到近代概率。
- 1899年,高尔顿出版数理统计著作《自然的遗传》,引入回归分析方法,他给出回归直线和相关系数的重要概念。
- 1908年,英国统计学家哥赛特(Gosset)在Biometrics杂志上以笔名Student发表了使他名垂统计史册的论文:均值的或然误差。在这篇文章中,提出了「t分布」。t分布的发现在统计学史上具有划时代的意义,打破了正态分布一统天下的局面,开创了小样本统计推断的新纪元。后来,费希尔注意到他证明中的漏洞,并于1922年给出了此问题的完整证明,并编制了t分布的分位数表。
- 1909年-1920年,丹麦数学家、电气工程师A.K.Erlang用概率论方法研究电话通话问题,开创了「排队论」。
- 1920年,为了更准确地估计随机序列发展变化的规律,从20世纪20年代开始,学术界利用数理统计学原理分析时间序列。研究的重心从总结表面现象转移到分析序列值内在的关系上,由此开辟了一门应用统计学科——「时间序列分析」。
- …
1.4 概率论演化

2 在线学习
在线 概率与统计 视觉化学习 – 布朗大学
A visual introduction to probability and statistics
何志坚老师的数理统计讲义
何志坚,华南理工大学数学学院教授
鸢尾花书–统计至简
https://github.com/Visualize-ML/Book5_Essentials-of-Probability-and-Statistics文章来源:https://www.toymoban.com/news/detail-686575.html
参考
1、wiki–Probability theory
2、wiki–Theory of Probability and Mathematical Statistics
3、布朗大学 – A visual introduction to probability and statistics
4、何志坚,华南理工大学数学学院教授
5、生姜DrGinger
6、华中科技大学 – 统计学的历史
7、从博弈问题到方法论学科–概率论发展史研究
8、概率论与数理统计的前世今生
9、赵永红 – 概率论的起源、发展、应用
10、wiki – 概率论史
11、显著性检验、假设检验与零假设显著性检验
12、徐传胜 – 临沂师范学院数学系
13、概率论的历史简介
14、抽样分布篇之五:卡尔•皮尔逊和卡方分布
15、正态分布的发展与历史
16、显著性检验、假设检验与零假设显著性检验
17、从零开始学统计 03 | 均值,方差,标准差
18、数学基础–均值、方差、标准差、协方差文章来源地址https://www.toymoban.com/news/detail-686575.html
到了这里,关于概率论与数理统计发展历史简介的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!