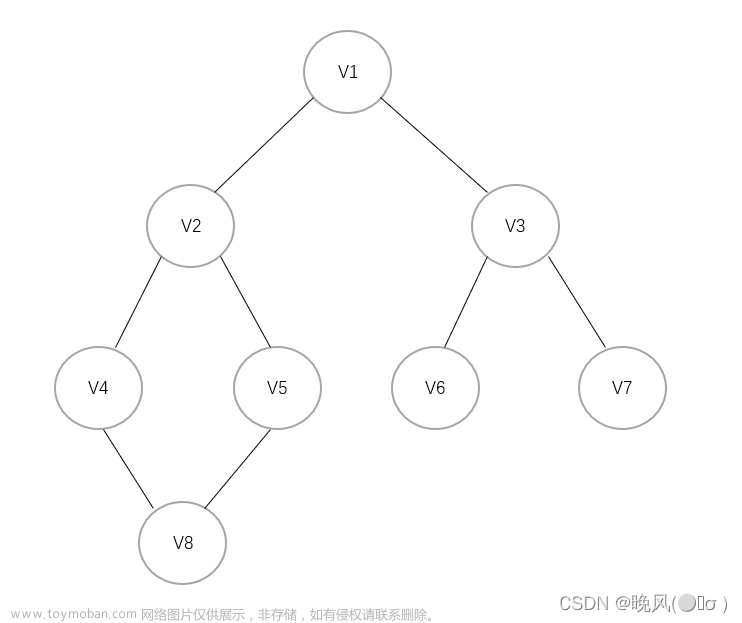
1.与树的深度优先遍历之间的联系
图的深度优先遍历类似于树的先根遍历(递归)。
树的先根遍历:
//树的先根遍历
void PreOrder(TreeNode *R) {
if (R != NULL) {
visit(R);
//访问根节点
while (R还有下一个子树T)//新找到的相邻结点一定是没有访问过的结点
Pre0rder(T);//先根遍历下一棵子树
}
}
2.算法实现
图的深度优先遍历
使用的逻辑结构是栈。
如果是非连通图,依旧无法遍历完所有结点。
所以,需要在遍历完一轮结点后,扫描未被标记的结点。
visited数组防止重复访问。
代码实现:
bool visited[MAX_VERTEX_NUM];//访问标记数组
void DFSTraverse(Graph G) {//对图G进行深度优先遍历
for (v = 0; v < G.vexnum; ++V)
visited[v] = FALSE;//初始化已访问标记数据
for (v = 0; v < G.vexnum; ++v)//本代码中是从v=0开始遍历
if (!visited[v])
DFS(G, v);
}
void DFS(Graph G, int v) { //从顶点v出发,深度优先遍历图G
visit(v);//访问顶点v
visited[v] = TRUE;//设已访问标记
for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighor(G, v, w))
if (!visited[w]) {// w为u的尚未访问的邻接顶点
DFS(G, w);
}
}
3.复杂度分析
1.空间复杂度
来自函数调用栈,最坏情况,递归深度为O(|V|)。最好情况,O(1)。
2.时间复杂度
时间复杂度=访问各结点所需时间+探索各条边所需时间。
- 邻接矩阵存储的图: 访问|V|个顶点需要O(V)的时间,查找每个顶点的邻接点都需要O(V)的时间,而总共有|V|个顶点时间复杂度=O(IV|2)。
- 邻接表存储的图:访问|V|个顶点需要O(|V|)的时间,查找各个顶点的邻接点共需要O(|E|)的时间,时间复杂度=O(|V|+|E|)。
4.深度优先生成树
每一个连通分量就是一颗深度优先生成树。文章来源:https://www.toymoban.com/news/detail-686774.html
- 同一个图的邻接矩阵表示方式唯一,因此深度优先遍历序列唯一,深度优先生成树也唯一。
- 同一个图邻接表表示方式不唯一,因此深度优先遍历序列不唯一,深度优先生成树也不唯一。
调用多次DFS后,就是深度优先生成森林。文章来源地址https://www.toymoban.com/news/detail-686774.html
5.图的遍历和图的连通性
1.对于无向图
- 调用BFS/DFS函数的次数=连通分量数。
- 对于连通图,只需调用1次BFS/DFS。
2. 对于有向图
- 调用BFS/DFS函数的次数要具体问题具体分析。
- 若起始顶点到其他各顶点都有路径,则只需调用1次BFS/DFS 函数。
- 对于强连通图,从任一结点出发都只需调用1次BFS/DFS。
到了这里,关于深度优先遍历(DFS)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!