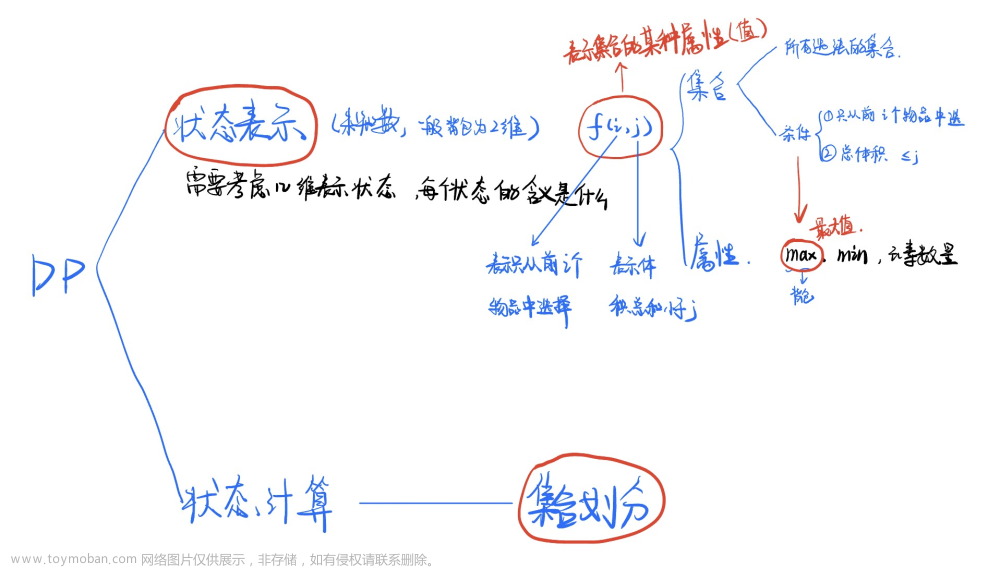
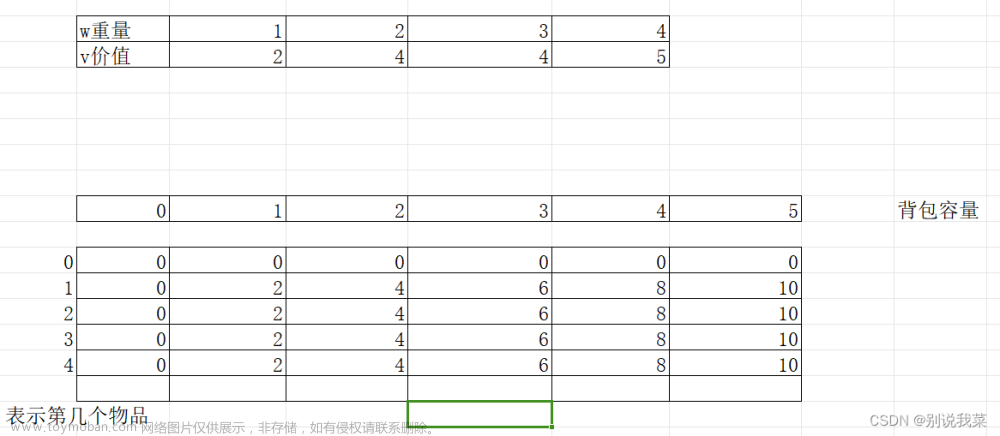
1.【模板】完全背包_牛客题霸_牛客网
你有一个背包,最多能容纳的体积是V。
现在有n种物品,每种物品有任意多个,第i种物品的体积为vivi ,价值为wiwi。
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
输入描述:
第一行两个整数n和V,表示物品个数和背包体积。
接下来n行,每行两个数vivi和wiwi,表示第i种物品的体积和价值。
1≤n,V≤10001≤n,V≤1000
输出描述:
输出有两行,第一行输出第一问的答案,第二行输出第二问的答案,如果无解请输出0。
示例1
输入:
2 6 5 10 3 1输出:10 2示例2
输入:
3 8 3 10 9 1 10 1输出:20 0说明:
无法恰好装满背包。示例3
输入:
6 13 13 189 17 360 19 870 14 184 6 298 16 242输出:596 189说明:
可以装5号物品2个,达到最大价值298*2=596,若要求恰好装满,只能装1个1号物品,价值为189.
#include <iostream>
#include <string.h>
using namespace std;
int main()
{
int n, V;
cin >> n >> V;
int v[n];
int w[n];
for (int i = 0; i < n; i++) cin >> v[i] >> w[i];
int dp[n + 1][V + 1];
//初始化
memset(dp, 0, sizeof dp);
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= V; j++)
{
//动态转移方程
dp[i][j] = dp[i - 1][j];
if (j - v[i - 1] >= 0) dp[i][j] = max(dp[i][j], dp[i][j - v[i - 1]] + w[i - 1]);
}
}
cout << dp[n][V] << endl;
memset(dp, 0, sizeof dp);
for (int i = 1; i <= V; i++) dp[0][i] = -1;
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= V; j++)
{
dp[i][j] = dp[i - 1][j];
if (j - v[i - 1] >= 0 && dp[i][j - v[i - 1]] != -1) dp[i][j] = max(dp[i][j], dp[i][j - v[i - 1]] + w[i - 1]);
}
}
cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;
return 0;
}2.零钱兑换 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回
-1。你可以认为每种硬币的数量是无限的。
示例 1:文章来源:https://www.toymoban.com/news/detail-687072.html
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1示例 2:
输入:coins =[2], amount =3输出:-1示例 3:
输入:coins = [1], amount = 0 输出:0
class Solution {
public:
int coinChange(vector<int>& coins, int amount)
{
int n=coins.size();
vector<int> dp(amount+1);//创建dp表
for(int i=1;i<=amount;i++) dp[i]=0x3f3f3f3f;//初始化,寻找最小值
for(int i=1;i<=n;i++)
{
for(int j=coins[i-1];j<=amount;j++)
{
if(j-coins[i-1]>=0)
{
dp[j]=min(dp[j],dp[j-coins[i-1]]+1);//动态转移方程
}
}
}
return dp[amount]>=0x3f3f3f3f?-1:dp[amount];//返回值
}
};3.零钱兑换二 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个整数数组
coins表示不同面额的硬币,另给一个整数amount表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回
0。假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5] 输出:4 解释:有四种方式可以凑成总金额: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1示例 2:
输入:amount = 3, coins = [2] 输出:0 解释:只用面额 2 的硬币不能凑成总金额 3 。示例 3:
输入:amount = 10, coins = [10] 输出:1
class Solution {
public:
int change(int amount, vector<int>& coins)
{
int n=coins.size();
vector<int> dp(amount+1);
dp[0]=1;//初始化
for(int i=1;i<=n;i++)
{
for(int j=coins[i-1];j<=amount;j++)
{
dp[j]+=dp[j-coins[i-1]];//动态转移方程
}
}
return dp[amount];//返回值
}
};4.完全平方数 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个整数
n,返回 和为n的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,
1、4、9和16都是完全平方数,而3和11不是。示例 1:
输入:n =12输出:3 解释:12 = 4 + 4 + 4示例 2:文章来源地址https://www.toymoban.com/news/detail-687072.html
输入:n =13输出:2 解释:13 = 4 + 9
class Solution {
public:
int numSquares(int n)
{
int m=sqrt(n);
vector<int> dp(n+1,0x3f3f3f3f);//初始化
dp[0]=0;
for(int i=1;i<=m;i++)
{
for(int j=i*i;j<=n;j++)
{
dp[j]=min(dp[j],dp[j-i*i]+1);//动态转移方程
}
}
return dp[n];
}
};到了这里,关于C++--完全背包问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!