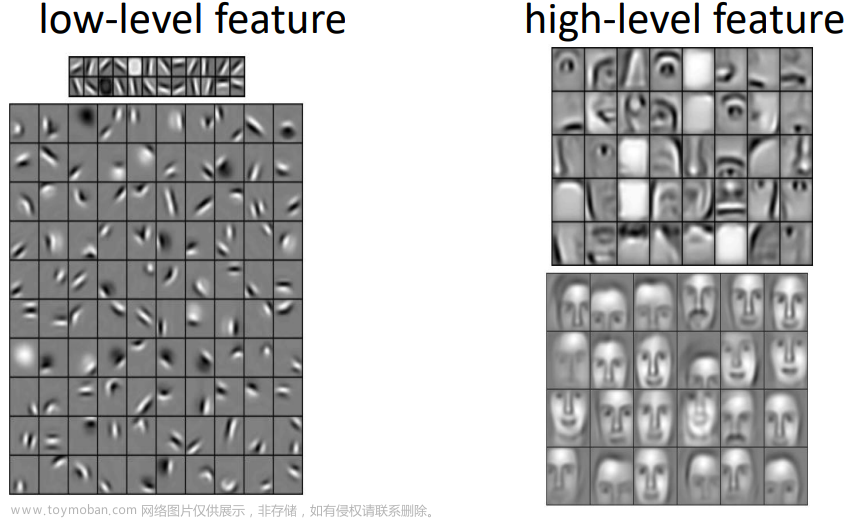
经过卷积神经网络(Convolutional Neural Network,CNN)处理后,图片的尺寸会发生变化,这是由于卷积层、池化层等操作引起的。计算图片经过卷积神经网络后的尺寸变化通常需要考虑卷积核大小、步幅(stride)、填充(padding)以及池化操作等因素。以下是计算过程的一般步骤:
假设输入图片的尺寸为 H in × W in H_{\text{in}} \times W_{\text{in}} Hin×Win,卷积核大小为 K × K K \times K K×K,步幅为 S S S,填充为 P P P。卷积操作会导致输出尺寸的变化,计算公式如下:
输出高度 H out = H in + 2 P − K S + 1 H_{\text{out}} = \frac{H_{\text{in}} + 2P - K}{S} + 1 Hout=SHin+2P−K+1
输出宽度 W out = W in + 2 P − K S + 1 W_{\text{out}} = \frac{W_{\text{in}} + 2P - K}{S} + 1 Wout=SWin+2P−K+1
填充可以是VALID(不填充)、SAME(填充以保持输入输出尺寸一致)等,步幅表示卷积核在输入上滑动的步长。
对于池化层,通常使用最大池化或平均池化。假设池化操作的大小为 P pool × P pool P_{\text{pool}} \times P_{\text{pool}} Ppool×Ppool,步幅为 S pool S_{\text{pool}} Spool,池化操作会导致输出尺寸的变化,计算公式如下:
池化后的输出高度 H out = H in − P pool S pool + 1 H_{\text{out}} = \frac{H_{\text{in}} - P_{\text{pool}}}{S_{\text{pool}}} + 1 Hout=SpoolHin−Ppool+1
池化后的输出宽度 W out = W in − P pool S pool + 1 W_{\text{out}} = \frac{W_{\text{in}} - P_{\text{pool}}}{S_{\text{pool}}} + 1 Wout=SpoolWin−Ppool+1文章来源:https://www.toymoban.com/news/detail-687732.html
这些计算方式可以用来预测经过卷积和池化操作后图片尺寸的变化。需要注意的是,不同层之间的尺寸变化会影响特征图的深度和尺寸,这在设计神经网络架构时需要仔细考虑。文章来源地址https://www.toymoban.com/news/detail-687732.html
到了这里,关于经过卷积神经网络之后的图片的尺寸如何计算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!