数学建模：层次分析法-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模：层次分析法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🔆 文章首发于我的个人博客：欢迎大佬们来逛逛

层次分析法

步骤描述

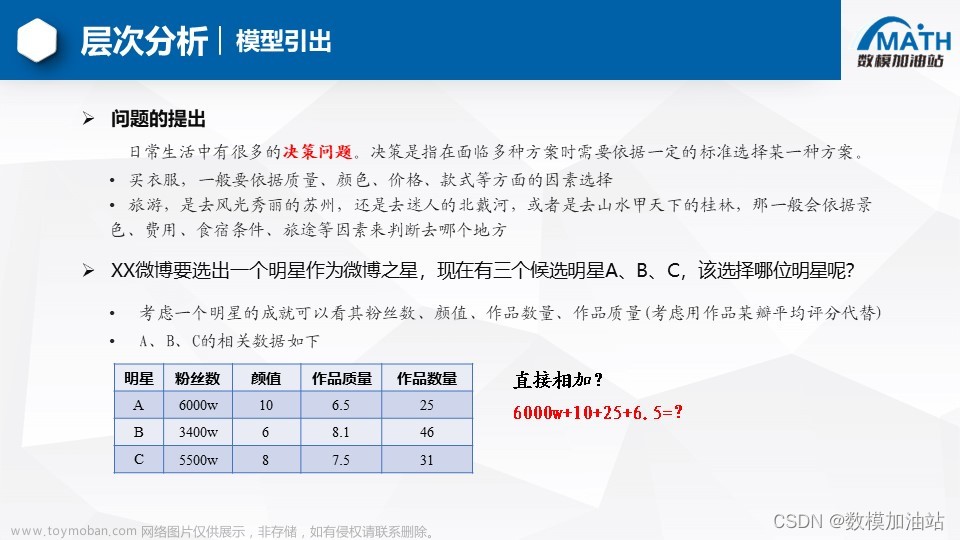
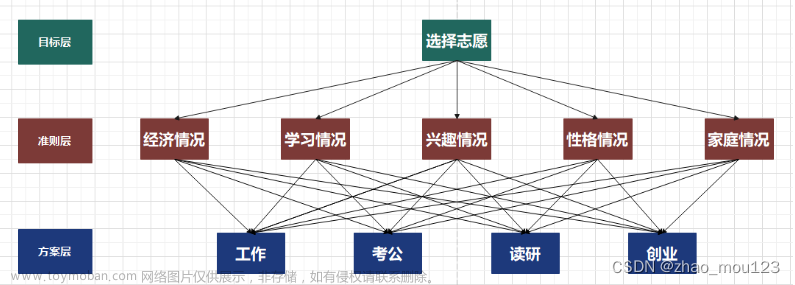
将问题条理化，层次化，构建出一个有层次的结构模型。层次分为三类：目标层，准则（指标）层，方案层。
比较指标层中不同指标之间的相对重要程度，并且构建一个成对比较矩阵。
1. 自行判断两个不同指标的相对重要程度。
2. 如果指标1重要程度大于指标2，并且赋予一个重要程度为3，因此得到其指标1的值为3，
3. 同理指标2的重要程度小于指标1（不能存在矛盾），因此相对的指标2的值为 $\frac{1}{3}$
4. 因此任意两个指标重要度之间存在的关系为： $a_{ij}>0，a_{ij} = \frac{1}{a_{ji}}，i,j\in(1,2,3,...n)$
5. 接着构建出所有两个指标的这种关系，就可以得到一个关于所有指标两两之间的成对比较矩阵 $A_{nn}$ ，其中 $n$ 为指标的数量。
在单一准则下计算指标相对排序的权重，以及进行判断矩阵（成对比较矩阵）的一致性检验
计算方案层中对于目标层的总排序权重，从而得到评价后的结果。

算法流程

通过分层与条理化后，我们得到了两两指标之间的成对比较矩阵（判断矩阵）：

$\left|\begin{array}{cccc}1 & 3 & 1 & 1 / 3 \\1 / 3 & 1 & 1 / 2 & 1 / 5 \\1 & 2 & 1 & 1 / 3 \\3 & 5 & 5 & 1\end{array}\right|$

首先得到判断矩阵的最大特征值对应的特征向量T：

$T=\begin{bmatrix}t_1&t_2&\cdots&t_n\end{bmatrix}$

得到权重向量W：

$\begin{gathered}W=\begin{bmatrix}w_1&w_2&\cdots&w_n\end{bmatrix}\\\\w_i=\frac{t_i}{\sum_{i=1}^nt_i}\end{gathered}$

计算一致性指标 $C I$

$I=\frac{\lambda_{\max }-n}{n-1}$

查找相应的随机平均一致性指标 $R I$ ：如果 $n = 5$ 则表示有五个指标，则 $R I = R I (1, 5) = 1.12$

数学建模：层次分析法,数学建模,MATLAB,数学建模

计算**一致性比例CR：**当 $CR < 0.10$ 时，一致性接受，否则改矩阵应该适当修改参数。

$\frac{CI}{RI}$

计算评价对象的得分：其中 $P$ 为归一化后的原始数据， $W$ 为权重向量

$\cdot W$

完整代码

function [Score,W] = mfunc_levelAnalysis(A,data)
    % 层次分析法：求解每个评价对象的综合得分与对应权重
    % paramts: 
    %      A: 两两指标之间的自定义的成对对角矩阵 Shape: (n,n)
    %      data: 原始数据矩阵,(m,n) m为评价对象，n为评价指标
    % returns:
    %      Score：每个评价对象的综合得分
    %      W: 所有指标的权重
    
    % 成对对角矩阵：A判别矩阵
    % A=[1,3,1,1/3;
    %     1/3,1,1/2,1/5;
    %     1,2,1,1/3;
    %     3,5,3,1];
    [n,~]=size(data);
    %Z=zscore(X);
    Z = data ./ repmat(sum(data.*data) .^ 0.5, n, 1); %矩阵归一化
    
    [n,~]=size(A);
    %求特征值特征向量,找到最大特征值对应的特征向量
    [V,D]=eig(A);
    tzz=max(max(D));     %找到最大的特征值
    c1=find(D(1,:)==tzz);%找到最大的特征值位置
    T=V(:,c1);%最大特征值对应的特征向量
    %赋权重
    W=zeros(n,1);
    for i=1:n
    W(i,1)=T(i,1)/sum(T);
    end
    %一致性检验
    CI=(tzz-n)/(n-1);
    RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
    %判断是否通过一致性检验
    CR=CI/RI(1,n);
    if CR>=0.1
       fprintf('没有通过一致性检验\n');
    else
      fprintf('通过一致性检验\n');
    end
     score=Z*W;
     Score=100*score/max(score);
end