目录
1 从颜色说起
1.1 用简单的枚举 → 一一映射到某种颜色
1.1.1 自然语言里的颜色对应
1.1.2 举个例子：VB里的colorindex
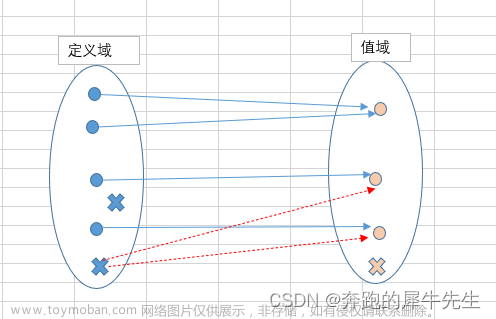
1.1.3 接下来的关键问题就是：如何对应更多的颜色，无限穷举么?
1.2 升级版的颜色映射思路：RGB颜色
1.2.1 RGB颜色大家都明白原理
1.2.2 表达方式1：用一个16*6的矩阵来表示颜色
1.2.3 表达方式2： 用(red,green,blue) 这3个维度组成一个向量来表示颜色
1.2.4 总结，RGB颜色就是用矩阵的形式来表示颜色了
1.2.5 附属知识
(1) 十六进制
(2) 颜色的RGB值
（3） 一些颜色的其他概念
1.3 从RGB颜色向量组，引出向量空间的基
2 向量空间的基（basis）：向量空间的的基础 / 轴
2.1 什么样的向量可以做基？
2.2 基的分类
2.2.1 不同空间的基---向量组的数量可能不同
2.2.2 自然基
2.2.3 正交基
2.2.4 标准正交基
2.2.5 基和向量/矩阵
3 基变换
（1）基不变，坐标变换
（2）坐标不变，基变换
3.1.6 基变换和坐标变换的公式 （待完成）
1 从颜色说起
- 如何显示颜色，以前的人有过很多的尝试
- 最简单的思路就是枚举和映射，1种颜色对应1个代码/数字，其实和密码也差不多
1.1 用简单的枚举 → 一一映射到某种颜色
1.1.1 自然语言里的颜色对应
其中举例最简单的就是语言
- red--红色--1
- green---绿色---2
- blue--红色--3
- yellow--黄色色--4
- 。。。
1.1.2 举个例子：VB里的colorindex
- colorindex是EXCEL的颜色代码，一共就56个颜色
- 但实际上VBA里还有RGB颜色代码 color=rgb(,,) ， TextBox1.BackColor=rgb()
Sub test_color()
Range("i6:i19")).Interior.ColorIndex
For Each i In Range("B1:H19")
i.Offset(0, 1).Interior.ColorIndex = i.Value
Next
'第一次想到的这种思路不行Union(Range("c6:c19"), Range("E6:E19"), Range("G6:G19"))
End Sub
1.1.3 接下来的关键问题就是：如何对应更多的颜色，无限穷举么?
- 自然语言里的颜色，一般也就十来种，几十种都够难记难用了
- 像VBA里的colorindex() 的56种颜色，虽然已经够多了，但是实际上专业的人还是觉得不够用
- 所以，枚举加到几百，上千去？
1.2 升级版的颜色映射思路：RGB颜色
1.2.1 RGB颜色大家都明白原理
- 实际上就是 red, green,blue 这3元色来生成其他颜色
- RGB颜色有2种数字化 表示方式
- 比如 ffffff 000000 ，这个是16进制数字来表示颜色
- 使用RGB的向量值来表示其他颜色的，比如 黑色是(0,0,0) ,白色是(255,255,255), 而后面这种方法，就是向量和矩阵的方法
1.2.2 表达方式1：用一个16*6的矩阵来表示颜色
- 其实ffffff这种，表面也是用一个维度的一串数字来表示不同的颜色
- 但是和前面不同的就是，只有固定的6位
- 所以要表示多种颜色，相当于其列向量=6个，行向量=16，可以看成一个A16*6 的矩阵。
- 这个矩阵A16*6，最大容量16^6=16777216
1.2.3 表达方式2： 用(red,green,blue) 这3个维度组成一个向量来表示颜色
- RGB值从0-255，实际这个数字代表亮度
- RGB=(0,0,0) ,RGB=(100,100,100),这种形式是很明显的向量了
- 这个矩阵A256*3，即256*256*256种，颜色最大容量256^3=16777216
1.2.4 总结，RGB颜色就是用矩阵的形式来表示颜色了
- 本质都是用矩阵/向量组来表示颜色
1.2.5 附属知识
(1) 十六进制
（常用数字0、1、2、3、4、5、6、7、8、9和字母A、B、C、D、E、F（a、b、c、d、e、f）表示，其中:A~F表示10~15，这些称作十六进制数字。）
(2) 颜色的RGB值
RGB色彩模式是工业界的一种颜色标准，是通过对红（R）、绿（G）、蓝（B）三个颜色通道的变化以及它们相互之间的叠加来得到各式各样的颜色的，RGB即是代表红、绿、蓝三个通道的颜色，这个标准几乎包括了人类视力所能感知的所有颜色，是运用最广的颜色系统之一。
- RGB值从0-255，实际这个数字代表亮度
- 总共有256*256*256种，
| 颜色名称 |
红色值 Red |
绿色值 Green |
蓝色值 Blue |
||||
| 黑色 |
0 |
0 |
0 |
||||
| 蓝色 |
0 |
0 |
255 |
||||
| 绿色 |
0 |
255 |
0 |
||||
| 青色 |
0 |
255 |
255 |
||||
| 红色 |
255 |
0 |
0 |
||||
| 亮紫色（洋红色） |
255 |
0 |
255 |
||||
| 黄色 |
255 |
255 |
0 |
||||
| 白色 |
255 |
255 |
255 |
||||
（3） 一些颜色的其他概念
一些颜色显示的
- 16位色的发色总数是65536色，也就是2的16次方；
- 24位色被称为真彩色，它可以达到人眼分辨的极限，发色数是16777216色，也就是2的24次方。32位色就并非是2的32次方的发色数，它其实也是16777216色，不过它增加了256阶颜色的灰度也就是8位透明度，发色数其实2的24次方，但是增加了8位透明度，就规定它为32位色。
- 少量显卡能达到36位色，它是24位发色数再加512阶颜色灰度。
1.3 从RGB颜色向量组，引出向量空间的基
- 用RGB的第2种表示方法，用red,green,blue这3种颜色来生成其他所有颜色的向量空间
- 使用RGB的向量值来表示其他颜色的，比如 黑色是(0,0,0) ,白色是(255,255,255), 而后面这种方法，就是向量和矩阵的方法
- 实际上 RGB 是三原色，也就是 颜色空间/ 可以看成一个3维空间的基
- 其中 red 是 green 是 ，blue是
- 任意一种颜色都可以写成 red,green,blue的线性组合
- 也就是red,green,blue 是这个向量空间的一组 最大线性无关向量组，也是一组基。
- 而且因为red,green,blue这3个向量选择的特殊性，这3个向量组的基，还是自然基，也是正交基！
2 向量空间的基（basis）：向量空间的的基础 / 轴
2.1 什么样的向量可以做基？
向量空间的基的严格定义：向量空间中的某组向量 A= {a1,a2.....an} ，这些向量如果是这个向量空间的最大线性无关组，那么这组向量A就是这个空间的一组基。
总结可以做基的特征
A= {a1,a2.....an} 这组向量，或这个向量组
- 必须是线性无关的。
- 而且必须是这个空间的最大线性无关组。
理论上，颜色空间的基有无数组，但是很多向量组也不能作为基本
举例
- 比如RG这2种颜色构成的向量组，不能称为RGB空间的一组基，因为RG组成不了所有颜色
- 比如线性相关的3组向量: 深绿色(0,255,0)，标准绿色(0,100,0) 和蓝色(0,0,255)不能作为颜色空间的基的，因为3个线性相关的颜色基，无法组成所有颜色。
2.2 基的分类
2.2.1 不同空间的基---向量组的数量可能不同
- （a1,a2）是2维的，对应2个基底e1,e2
- （a1,a2,a3）是3维的，对应3个基底e1,e2,e3
- （a1,a2,a3... ... an）是n维的, 对应n个基底e1,e2.....en
2.2.2 自然基
- 自然基本特指这种
- 自然基，比然是正交基，也是标准正交基
2.2.3 正交基
- 基这组向量里的每个向量都是互相 垂直/正交的
2.2.4 标准正交基
- 基这组向量里的每个向量都是互相 垂直/正交的
- 且长度都为1
- 标准正交基有很多，并不只是只有自然基那一组！
2.2.5 基和向量/矩阵
- 比如一个向量(3,2,5) 就可以认为是，这个向量的3个元素分别在3个基上的长度/伸缩度
- 向量(3,2,5) 在第1个基，(1,0,0) 上的长度/伸缩度是3，
- 向量(3,2,5) 在第2个基，(0,1,0) 上的长度/伸缩度是2，
- 向量(3,2,5) 在第3个基，(0,0,1) 上的长度/伸缩度是5，
3 基变换
- 矩阵的 基 / 基底 是可以改变的
- 实际上Ax=y 就可以看作 基变换
- Ax=y 有两种方法，要么坐标变，要么坐标不变，基变化
文章来源：https://www.toymoban.com/news/detail-689247.html
（1）基不变，坐标变换
- 假设我们有A是e1,e2,e3 等 自然基下的向量x
- 计算 A*x=y
- 一般我们计算 A*x=y 其实都是将 向量x 经过矩阵A变换后，生成了新的向量y，而新的向量y实际就是原向量的坐标发生了变化，其仍然是e1,e2。。。等 自然基下的向量y
（2）坐标不变，基变换
- 假设我们有A是e1,e2。。。等自然基下的向量x
- 而A的列向量分别是 α1,α2 ....
- 计算 A*x=y
- 我们可以保持x向量的坐标还是老的，但是基不再用e1,e2。。。等，而是用A的列向量α1,α2 ....作为新的基.
3.1.6 基变换和坐标变换的公式 （待完成）
文章来源地址https://www.toymoban.com/news/detail-689247.html
到了这里，关于线性代数的学习和整理17：向量空间的基，自然基，基变换等（未完成）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
