（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述-Toy模板网

这篇具有很好参考价值的文章主要介绍了（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

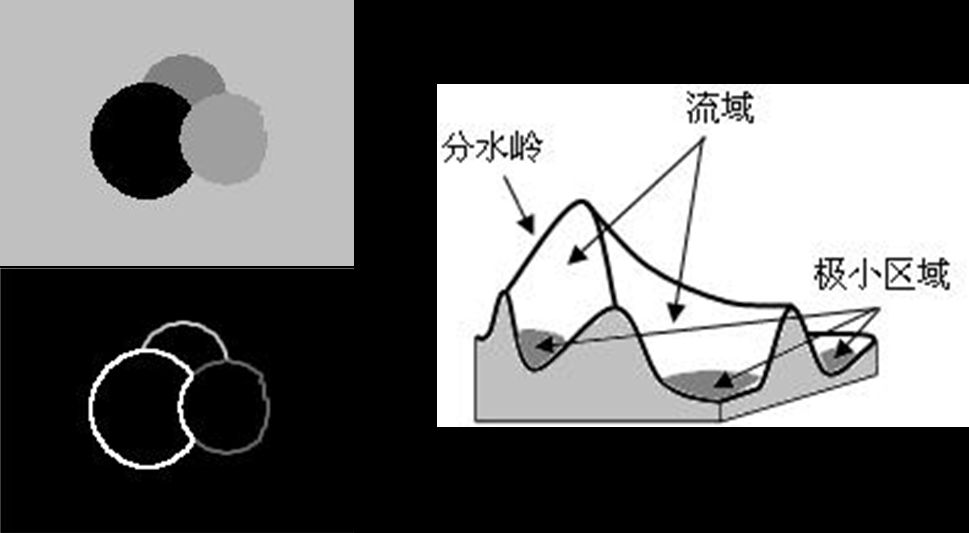
一：边界描述

（1）边界链码

A：概述

边界链码：是一种用于图像处理和计算机视觉领域的技术，主要用于描述二进制图像中物体的轮廓。边界链码通过将轮廓转化为一系列有序的连续像素点来表示。边界链码的基本思想是从图像中选择一个起始点，然后按照一定的顺序遍历相邻像素，将它们连接起来形成一个闭合的轮廓。这些相邻像素的连接方式可以根据具体的算法不同而有所差异，常见的有4邻域链码和8邻域链码

（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述,MATLAB+Python数字图像处理教程,matlab,python,图像处理

如下图，以左下角0点为起始点，设其坐标为（0,3），4方向和8方向链码表示区域边界，则

4方向链码：（0,3）0 0 0 1 1 1 2 3 2 3 2 3
8方向链码：（0,3）0 0 0 2 2 2 4 5 5 6

（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述,MATLAB+Python数字图像处理教程,matlab,python,图像处理

边界链码特点如下

由于表示一个方向数比表示一个坐标值所需比特数少，而且对每一个点又只需一个方向数就可以代替两个坐标值，因此链码表达可大大减少边界表示所需的数据量
可以很方便地获取相关几何特征，如区域的周长
隐含了区域边界的形状信息

边界链码缺点如下

码串比较长
噪声等干扰会导致小的边界变化，从而使链码发生与目标整体形状无关的较大变动
目标平移时，链码不变，但目标旋转时，链码会发生变化

B：边界链码改进

多重网格采样：对原边界以较大的网格重新采样，并把与原边界点最接近的大网格点定为新的边界点。也可用于消除目标尺度变化链码的影响

（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述,MATLAB+Python数字图像处理教程,matlab,python,图像处理

边界链码的起点：起点不同，链码不同。把链码归一化可解决这个问题

给定一个从任意点开始产生的链码，把它看作一个由各方向数构成的自然数
将这些方向数依一个方向循环，以使它们所构成的自然数的值最小；
将转换后所对应的链码起点作为这个边界的归一化链码的起点

一阶差分链码：链码中相邻两个方向数按反方向相减（后一个减前一个），目标发生旋转时，一阶差分链码不发生变化

（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述,MATLAB+Python数字图像处理教程,matlab,python,图像处理

C：程序

如下，统计边界链码，并利用链码重构目标区域边界

（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述,MATLAB+Python数字图像处理教程,matlab,python,图像处理

matlab：

clear,clc,close all;
image=imread('morphplane.jpg');
figure,imshow(image),title('ÔÍ¼');
BW=im2bw(image);
[B,L]=bwboundaries(1-BW);
len=length(B);
chain=cell(len,1);
startpoint=zeros(len,2);
for i=1:len
    boundary=B{i};
    everylen=length(boundary);
    startpoint(i,:)=boundary(1,:);
    for j=1:everylen-1
        candidate=[0 1;-1 1;-1 0;-1 -1;0 -1;1 -1;1 0;1 1];
        y=boundary(j+1,1)-boundary(j,1);
        x=boundary(j+1,2)-boundary(j,2);       
        [is,pos]=ismember([y x],candidate,'rows');     
        chain{i}(j)=pos-1;             
    end    
end
figure,imshow(L),title('»æÖÆÁ´Âë');
hold on
for i=1:len
    x=startpoint(i,2);
    y=startpoint(i,1);
    plot(x,y,'r*','MarkerSize',12);
    boundary=chain{i};
    everylen=length(boundary);
    for j=1:everylen
        candidate=[y x+1;y-1 x+1;y-1 x;y-1 x-1;y x-1;y+1 x-1;y+1 x;y+1 x+1];
        next=candidate(boundary(j)+1,:);
        x=next(2);y=next(1);
        plot(x,y,'g.');
    end
end

python：

import numpy as np
import matplotlib.pyplot as plt
from skimage import io, color, measure

# 读取图像
image = io.imread('morphplane.jpg')
plt.imshow(image)
plt.title('原始图片')
plt.show()

# 图像二值化处理
bw = color.rgb2gray(image) > 0.5

# 提取边界
boundaries = measure.find_boundaries(1 - bw)

# 获取边界链码
chain = []
startpoints = []

for boundary in measure.find_contours(boundaries, 0.5):
    startpoint = boundary[0].astype(int)
    startpoints.append(startpoint)
    
    chain_segment = []
    for i in range(len(boundary)-1):
        y = boundary[i+1, 0] - boundary[i, 0]
        x = boundary[i+1, 1] - boundary[i, 1]
        
        candidate = np.array([[0, 1], [-1, 1], [-1, 0], [-1, -1], [0, -1], [1, -1], [1, 0], [1, 1]])
        pos = np.where((candidate == [y, x]).all(axis=1))[0][0]
        
        chain_segment.append(pos)
    
    chain.append(chain_segment)

# 显示边界链码
fig, ax = plt.subplots()
ax.imshow(boundaries)
ax.set_title('边界链码')
for i in range(len(startpoints)):
    startpoint = startpoints[i]
    ax.plot(startpoint[1], startpoint[0], 'r*', markersize=12)
    boundary = chain[i]
    y, x = startpoint
    
    for j in range(len(boundary)):
        candidate = np.array([[y, x+1], [y-1, x+1], [y-1, x], [y-1, x-1], [y, x-1], [y+1, x-1], [y+1, x], [y+1, x+1]])
        next_point = candidate[boundary[j]]
        x, y = next_point
        ax.plot(x, y, 'g.')

plt.show()

（2）傅里叶描绘子

A：概述

傅里叶描绘子：是一种常用于形状描述和图像处理的数学方法。它利用傅里叶变换的思想，将一个封闭曲线或轮廓分解为一系列频谱成分，从而对形状进行表示和比较。傅里叶描绘子的基本原理是将曲线表示为一系列复数，每个复数代表了曲线上的一个点。通过对这些复数进行傅里叶变换，可以得到频谱信息。在傅里叶变换中，高频成分表示了曲线的细节和局部特征，低频成分表示了曲线的整体形状。其计算步骤如下

对封闭曲线或轮廓进行采样，获取一系列坐标点
将坐标点转换为复数形式，即将每个点的 $x$ 和 $y$ 坐标看作是实部和虚部构成的复数
对复数序列进行离散傅里叶变换（DFT），得到频域表示
根据需要选择保留的频率成分，可以通过截断高频成分来降低数据量或者提取感兴趣的特征
对保留的频率成分进行逆傅里叶变换（IDFT），得到原始坐标点的复数表示
将复数表示转换为实部和虚部，得到重建后的坐标点

通过傅里叶描绘子，可以对形状进行压缩、匹配和比较。由于傅里叶变换具有平移、旋转和尺度不变性，因此傅里叶描绘子也具有这些不变性，使得它在形状识别、目标跟踪和图像检索等领域有广泛应用

B：程序

如下，分割图像，计算各区域边界点的傅里叶描绘子并重建边界

（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述,MATLAB+Python数字图像处理教程,matlab,python,图像处理

matlab：

Image=rgb2gray(imread('bricks.jpg'));
figure,imshow(Image),title('原始图像');
T=graythresh(Image);                     %获取阈值T
result=im2bw(Image,T);                   %二值化图像
S=zeros(size(Image));
[B,L]=bwboundaries(1-result);
for k=1:length(B) 
    N=length(B{k});
    if N/2~=round(N/2)
        B{k}(end+1,:)=B{k}(end,:);
        N=N+1;
    end
    z=B{k}(:,2)+1i*B{k}(:,1);    
    for m=[N/2 N*24/32 N*60/64 N*126/128]
        Z=fft(z);
        [Y,I]=sort(abs(Z));
        for count=1:m
            Z(I(count))=0;
        end
        zz=ifft(Z);
        figure,imshow(S);
        hold on;
        plot(real(zz),imag(zz),'w');
    end
end

python：

import numpy as np
import matplotlib.pyplot as plt
from skimage import io, color, filters

# 读取图像并转为灰度图像
image = color.rgb2gray(io.imread('bricks.jpg'))
plt.imshow(image, cmap='gray')
plt.title('原始图像')
plt.show()

# 二值化图像
threshold = filters.threshold_otsu(image)
result = image > threshold

# 初始化画布
S = np.zeros_like(image)

# 获取边界
boundaries = color.label2rgb(result, image, kind='overlay')
contours = measure.find_contours(result, 0.5)

# 绘制傅里叶描绘子
for contour in contours:
    N = len(contour)
    if N % 2 != 0:
        contour = np.append(contour, [contour[-1]], axis=0)
        N += 1
    
    z = contour[:, 1] + 1j * contour[:, 0]
    
    for m in [N/2, N*24/32, N*60/64, N*126/128]:
        Z = np.fft.fft(z)
        I = np.argsort(np.abs(Z))
        
        for count in range(int(m)):
            Z[I[count]] = 0
        
        zz = np.fft.ifft(Z)
        
        plt.imshow(S, cmap='gray')
        plt.hold(True)
        plt.plot(np.real(zz), np.imag(zz), 'w')
        plt.show()

二：矩描述

（1）矩

A：几何矩

几何矩：是一种用于描述图像或形状的数学特征。它们通过对图像或形状的像素值及其位置进行加权求和来计算，提供了关于形状的位置、大小、方向以及形态特征的信息。几何矩的计算基于图像或形状的二维坐标系，并使用不同的权重函数来表示不同的特征

一阶几何矩：是形状的质心（centroid），它表示形状的位置信息
二阶几何矩：包括中心距（central moments），可以获得形状的尺寸和形态特征，例如面积、面积矩、最大、最小轴长和方向等
三阶几何矩和高阶几何矩：提供了更丰富的形态信息，如形状的对称性、弯曲程度等

几何矩计算公式如下

零阶几何矩（面积）： $M_{00} = \sum \sum I(x, y)$
一阶几何矩（质心）： $M_{10} = \sum \sum x \cdot I(x, y), \quad M_{01} = \sum \sum y \cdot I(x, y)$
二阶几何矩（中心矩）： $\mu_{20} = \sum \sum (x - x_c)^2 \cdot I(x, y), \quad \mu_{02} = \sum \sum (y - y_c)^2 \cdot I(x, y), \quad \mu_{11} = \sum \sum (x - x_c)(y - y_c) \cdot I(x, y)$

B：不变矩组

不变矩组：是一种用于图像处理和模式识别的特征描述方法。它基于几何矩的概念，通过对图像或形状的几何矩进行归一化和旋转不变性的处理，生成一组具有唯一性和稳定性的特征向量，用于表示和比较图像或形状。计算步骤如下

将图像或形状转换为灰度图像，并对其进行二值化处理
计算二值化图像的几何矩，包括零阶、一阶和二阶矩
根据几何矩计算归一化中心矩，将几何矩除以零阶矩的幂次来消除尺度的影响
根据归一化中心矩计算不变矩，通过对几何矩进行线性组合和归一化得到一组不变矩
对不变矩进行平移、旋转和缩放等操作，使其具有平移和旋转不变性

（2）与矩相关的特征

A：二阶矩

二阶矩：也称为方差（Variance），是统计学中常用的描述数据分布离散程度的指标。在图像处理和模式识别中，二阶矩被广泛应用于描述图像的纹理特征和灰度分布特性。对于一维数据集，二阶矩定义为每个数据点与数据集均值之差的平方的平均值。对于二维数据集或图像，二阶矩是对数据点与数据集均值之差的平方的期望

$\left\{\begin{array}{l}M_{20}=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} x^{2} f(x, y) \\M_{02}=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} y^{2} f(x, y)\end{array}\right.$

B：主轴

主轴：是指图形、形状或区域的特征轴线，它描述了形状的主要方向和旋转情况。主轴通常使用惯性矩阵来计算，通过分析图像或形状在不同方向上的质量分布来确定主轴的方向和长度

（数字图像处理MATLAB+Python）第十一章图像描述与分析-第五、六节：边界描述和矩描述,MATLAB+Python数字图像处理教程,matlab,python,图像处理

C：等效椭圆

等效椭圆：是用于描述图形或形状的一种几何模型，它能够近似地表示原始图形的外形和尺寸。等效椭圆通常是通过对图形的边界进行拟合得到的，使得椭圆与图形的形状最相似

$\left\{\begin{array}{l}\left.a=\left[\frac{2\left(\mu_{20}+\mu_{02}+\sqrt{\left(\mu_{20}-\mu_{02}\right)^{2}+4 \mu_{11}^{2}}\right)^{\frac{1}{2}}}{\mu_{00}}\right]^{\frac{1}{2}}\right]^{\frac{1}{2}} \\b=\left[\frac{2\left(\mu_{20}+\mu_{02}-\sqrt{\left(\mu_{20}-\mu_{02}\right)^{2}+4 \mu_{11}^{2}}\right.}{\mu_{00}}\right]^{\frac{1}{2}}\end{array}\right.$