动态规划之连续乘积最大子数组 & 连续和最大子数组-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划之连续乘积最大子数组 & 连续和最大子数组。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一. 连续和最大子数组

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组是数组中的一个连续部分。
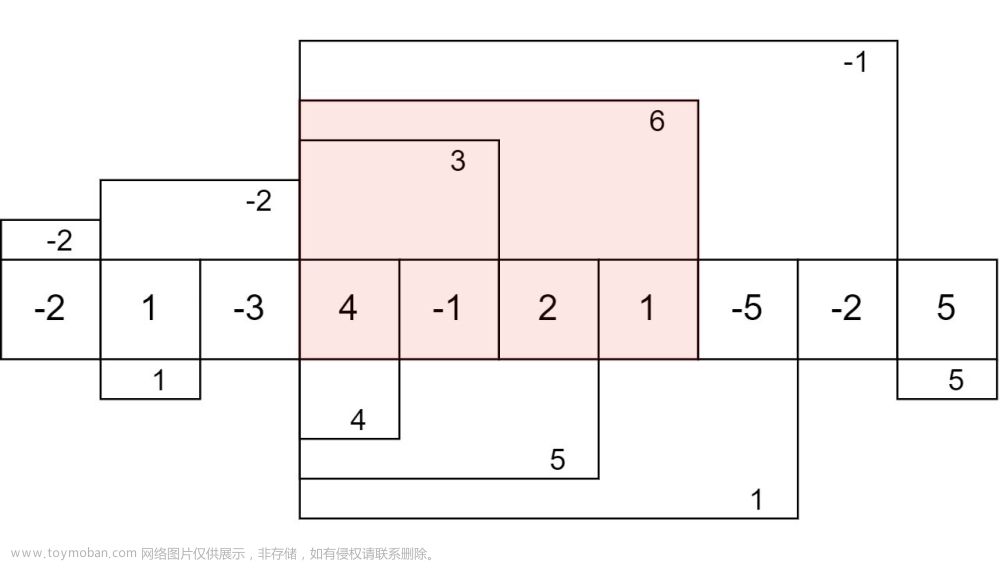
示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

1.1 怎么想到使用动态规划？

当然是题目给的建议。

题目中讲，求最大和。
题目中讲，返回最大和。

我们要做的是求一个目标值（通常最大，最小），不要求过程，只要结果。对于这种题目，我们通常使用动态规划。

1.2 动态规划第一步该做什么？

首先明确几个关键点。

最大连续子数组，与子序列区别开，即数组下标连续。
和最大，针对每个【i】怎么计算子问题。

当然就是找到状态转移方程啊！

$=\left\{ \begin{aligned} f(i-1) + i (i <= f(i-1) + i) \\ i (i > f(i-1) + i) \end{aligned} \right.$

求和的状态转移方程很简单。当我们有了 i - 1位置的结果，去求 i位置的连续子数组和，当然就是用 $f (i - 1) + i 和 i$ 比较一下，拿最大的呀

仔细想想，这不对吧？
动态规划之连续乘积最大子数组 & 连续和最大子数组,刷题笔记,动态规划,算法
这有什么不对的呢？

动态规划之连续乘积最大子数组 & 连续和最大子数组,刷题笔记,动态规划,算法
明显，前4个最大连续和是 1 + 2 + 3 = 6。

所以错在哪里了呢？或者说，我们怎么计算能得到6呢？

…

很简单，return 2 > 6 ? 2 : 6 不就行了吗

我们的函数计算的值是以当前坐标为结尾的数组的最大子数组。
动态规划的子问题和整体问题求的目标是一致的，只有状态再更迭，此处的状态就是下标index。

计算得到函数要与旧的最大值进行比较取最大。

fun maxSubArray(nums []int) int {
	pre, res := 0, nums[0]
	for _, v := range nums {
		pre = max(pre + v, v)
		res = max(res, pre)
	}
	return res
}

二. 连续乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位整数。
子数组是数组的连续子序列。

示例 1:

输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:

输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

2.1 这个题目使用什么方法？

乘积最大。
返回乘积。
连续子数组。

这俩题目，是不是一样的。先想一想差别。

求最大值，返回结果，那使用动态规划没什么问题。

2.2 直接写代码

fun maxSubArray(nums []int) int {
	pre, res := 1, nums[0]
	for _, v := range nums {
		pre = max(pre * v, v)
		res = max(res, pre)
	}
	return res
}

因为乘法，所以pre初始值改为1 。

会有问题吗？

动态规划之连续乘积最大子数组 & 连续和最大子数组,刷题笔记,动态规划,算法
明显的错误…

只是加法变乘法，原来的方案就行不通了。

问题就在于，乘法遇到负数，从最大变成了最小，-4 * 3 = -12

所以我们需要对这个负号进行一下特殊的处理。

2.3 状态该怎么变化呢？

如果遇到负数，我们希望使用一个最小的值与其做乘积运算，期望得到一个最大的值；反之遇到正数，我们要用一个最大的值进行乘积运算。

所以，我们需要记两个值，分别是一个最大的preMax 和一个最小的preMin.

$preMax = f(i)_{max} \\ preMin = f(i)_{min}\\ preMax = Max(f(i-1)_{max}*num[i], f(i-1)_{min} * num[i], num[I])\\ preMin= Min(f(i-1)_{min}*num[i], f(i-1)_{max} * num[i], num[I])$

代码就比较简单了

func maxProduct(nums []int) int {
    preMax,preMin, res := 1,1, nums[0]
    for _,v := range nums {
    	mn,mx := preMin,preMax
    	preMax = max(mx * v, max(mn * v,v))
    	preMin = min(mn * v, min(mx * v,v))
    	res = max(preMax,res)
    }
    return res