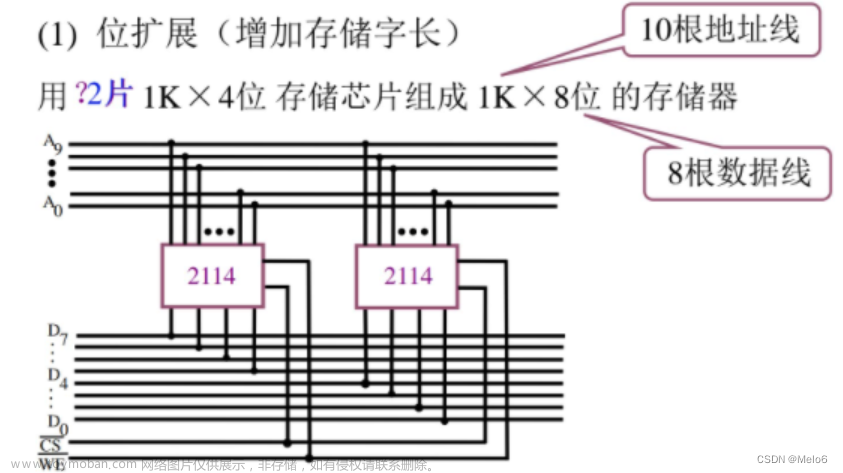
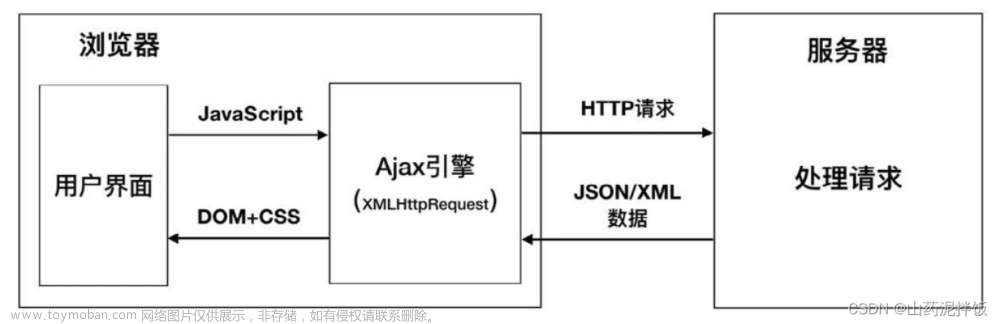
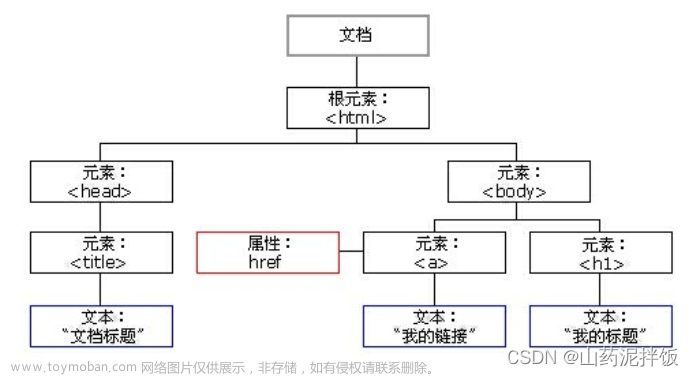
本章主要考察方法性的技巧，对于某些理论性的概念，建议在练习中加强理解，不定积分的要义在于不断练习、不断拓宽眼界
一.不定积分的概念
二.原函数存在定理
三.不定积分的定义
四.基本积分表
五.不定积分的性质
六.一类换元法
七.二类换元法
八.换元法的常用公式
九.分部积分法
十.有理函数的积分
十一.可化为有理函数的积分
十二.积分表的应用
根据牛顿-莱布尼茨公式，许多函数的定积分的计算就可以简便地通过求不定积分来进行。这里要注意不定积分与定积分之间的关系：定积分是一个数，而不定积分是一个表达式，它们仅仅是数学上有一个计算关系。一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。连续函数，一定存在定积分和不定积分；若在有限区间[a,b]上只有有限个间断点且函数有界，则定积分存在；若有跳跃、可去、无穷间断点，则原函数一定不存在，即不定积分一定不存在。
求函数f(x)的不定积分，就是要求出f(x)的所有的原函数，由原函数的性质可知，只要求出函数f(x)的一个原函数，再加上任意的常数C就得到函数f(x)的不定积分。
虽然很多函数都可通过如上的各种手段计算其不定积分，但这并不意味着所有的函数的原函数都可以表示成初等函数的有限次复合，原函数不可以表示成初等函数的有限次复合的函数称为不可积函数。利用微分代数中的微分Galois理论可以证明，如：xx ，sinx/x这样的函数是不可积的。
考研数学一大纲中对这一章的要求如下：
1.理解原函数的概念，理解不定积分和定积分的概念.
2.掌握不定积分的基本公式，掌握不定积分和定积分的性质及定积分中值定理，掌握换元积分法与分部积分法.
3.会求有理函数、三角函数有理式和简单无理函数的积分.
4.理解积分上限的函数，会求它的导数，掌握牛顿-莱布尼茨公式.
5.理解反常积分的概念，了解反常积分收敛的比较判别法，会计算反常积分.
6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值~
4.1不定积分的定义and积分表的使用
- 承前启后：作为求导的逆运算存在，且无上下限，添加后为定积分
- 原函数存在定理：连续一定有原函数——不同的原函数之间只相差常数C~
- 几何意义：一组上下变化的曲线簇~
- 对1积分，结果即为积分变量本身~
- secx求导为：tanx*secx
- cscx求导为：-cotx*cscx（一定要熟记~）
- 不定积分的加减可以拆分，乘除是无法拆分的
- secx的平方求导为tanx平方+1
- 二倍角公式，积化和差、和差化积，这些都是解决三角函数积分中最重要的公式，一定不能偷懒~
4.2第一类换元积分法
- 核心思想：微分号d之前的某一部分求出原函数直接拿到d的里面去（过程的本质即为连用两次微分公式~）
- d的里面可以任意地加减常数~
4.3第二类换元积分法
- 与一类换元的区别：一类积分朝外拿，二类求导朝里拿！
- 常用于凑出根号下的平方项，将根号消去~
- 常见的根号换元有3种：x=a*sint，x=a*sect，x=a*tant
- 常见的三角函数及其平方项的积分最好可以记住答案~
4.4分部积分法
- 构造函数时的重点是：U选择和V函数的选择~
- 通常情况下：要求V要容易取得，且VdU比UdV更容易求出~
- 选V的顺序：三角函数=指数函数>幂函数>对数函数>反函数 （ex的优先级最高~）
- 有时分布积分要使用2次起步~
- 要点在于越化简越简单
4.5有理函数的积分
- 待定系数法
- 可化为有理式的积分
文章来源：https://www.toymoban.com/news/detail-690711.html
文章来源地址https://www.toymoban.com/news/detail-690711.html
到了这里，关于高等数学啃书汇总重难点（四）不定积分的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
