目录
一、邻接矩阵（无向图）
二、邻接矩阵（有向图）
三、邻接矩阵（网）
四、邻接表（无向图）
五、邻接表（有向图）
——图的存储结构相比较线性表与树来说就复杂很多
——对于线性表来说，是一对一的关系，所以用数组或者链表均可简单存放。
树结构是一对多的关系，所以我们要将数组和链表的特性结合在一起才能更好的存放。
——我们的图，是多对多的情况，另外图上的任何一个顶点都可以被看作第一个顶点，任一顶点的邻接点之间不存在次序关系。
——因为任意两个顶点之间都可能存在联系，因此无法以数据元素在内存中的物理位置来表示元素之间的关系（内存物理位置是线性的，图的元素关系是平面的）
一、邻接矩阵（无向图）
考虑到图是由顶点和边或弧两部分组成，合在一起比较困难，那就是很自然地考虑到分为两个结构来分别存储。
顶点因为不区分大小、主次，所以用一个一维数组来存储是很不错地选择。
而边或弧由于是顶点与顶点之间的关系，一维数组肯定就搞不定了，那我们不妨考虑用一个二维数组来存储。
1、图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图的边或弧的信息。
我们可以设置两个数组，顶点数组为vertex[4] = {V0，V1，V2，V3}，边数组arc[4][4]为对称矩阵（0表示不存在顶点间的边，1表示顶点间存在边）。
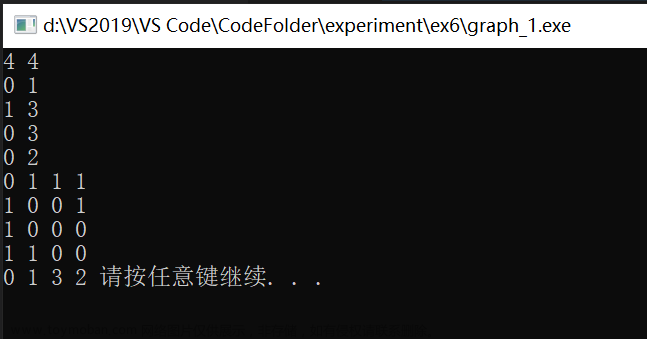
二、邻接矩阵（有向图）
可见顶点数组vertex[4]= {V0，V1，V2，V3}，弧数组arc[4][4]也是一个矩阵，但因为是有向图，所以这个矩阵并不对称，例如由V1到V0有弧，得到arc[1][0] = 1，而V0到V1没有弧，因此arc[0][1]=0。
另外有向图也是有讲究的，要考虑入度和出度，顶点V1的入度（横为出，竖为入）为1，正好是第V1列的个数之和，顶点V1的出度为2 ，正好是第V2行的个数之和。
三、邻接矩阵（网）
在图的术语中，我们提到了网这个概念，事实上也就是每条边上带有权的图就叫网。
这里 “∞” 表示一个计算机允许的，大于所有边上权值的值。
四、邻接表（无向图）
把数组与链表结合一起来存储，这种方式在图结构也适用，我们称为邻接表（AdjacencyList）。
邻接表的处理方法是：
1、图中顶点用一个一维数组存储，当然顶点也可以用单链表来存储，不过数组可以较为容易的读取顶点信息，更加方便。
2、图中每个顶点Vi的所有邻接点构成一个线性表，由于邻接点的个数不确定，所以我们选择用单链表来存储。文章来源：https://www.toymoban.com/news/detail-690819.html
五、邻接表（有向图）
邻接表结构类似无向图的。文章来源地址https://www.toymoban.com/news/detail-690819.html
到了这里，关于数据结构--5.0.1图的存储结构的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
