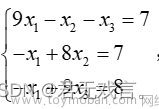求解线性方程组的G-S迭代法
// 运行不成功啊
function [x,k,index]= Gau_Seid(A,b,ep,it_max)
% 求解线性方程组的G-S迭代法,其中
% A为方程组的系数矩阵
% b为方程组的右端项
% ep为精度要求,省缺为1e-5
% it_max为最大迭代次数,省缺为100
% x为方程组的解
% k为迭代次数
if nargin <4 it_max = 100; end
if nargin <3 ep = 1e-5; end
n = length(A);
k = 0;
x = zeros(n,1);
y = zeros(n,1);
index = 1;
while 1
y = x;
for i = 1:n
z = b(i);
for j = 1:n
if j~=i
z = z-A(i,j)*x(j);
end
end
if abs(A(i,j))<1e-10 | k==it_max
index = 0;
return;
end
z = z/A(i,j);
x(i) = z;
end
if norm(y-x,inf)<ep
break;
end
k = k+1;
end
matlab中调用上述函数结果显示:
哪里出问题了啊?文章来源地址https://www.toymoban.com/news/detail-690864.html
文章来源:https://www.toymoban.com/news/detail-690864.html
到了这里,关于【学习笔记】求解线性方程组的G-S迭代法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!