R语言随机波动模型SV：马尔可夫蒙特卡罗法MCMC、正则化广义矩估计和准最大似然估计上证指数收益时间序列-Toy模板网

这篇具有很好参考价值的文章主要介绍了R语言随机波动模型SV：马尔可夫蒙特卡罗法MCMC、正则化广义矩估计和准最大似然估计上证指数收益时间序列。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

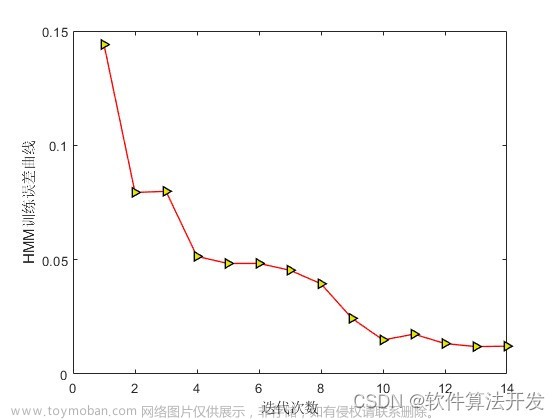
文章还展示了如何绘制上证指数收益时间序列图、散点图、自相关图与偏自相关图，并对数据进行了深入的分析。
本文做SV模型，选取马尔可夫蒙特卡罗法(MCMC)、正则化广义矩估计法和准最大似然估计法估计。

模拟SV模型的估计方法：

sim <- svsim(1000,mu=-9, phi = 0.97, sigma = 0.15)

print(sim)

summary(sim)

文章来源地址https://www.toymoban.com/news/detail-691694.html

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

plot(sim)

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

绘制上证指数收益时间序列图、散点图、自相关图与偏自相关图

我们选取上证指数5分钟高频数据：

data=read.csv("上证指数-5min.csv",header=TRUE)
#open：开盘价  close：收盘价 vol：成交量 amount：成交额
head(data,5)  #观察数据的头5行
tail(data,5)  #观察数据的最后5行
Close.ptd<-data$close
Close.rtd<-diff(log(Close.ptd))  #指标一：logReturn
rets=diff(data$close)/data$close[-length(data$close)]  #指标二：Daily Returns，我们选择Daily Returns
library(tseries)
adf.test(rets)

## 绘制上证指数收益时间序列图、散点图、自相关图与偏自相关图
Close.ptd.ts<-ts(Close.ptd,start=c(2005,1,4),freq=242)  
plot(Close.ptd.ts, type="l",main="(a) 上证指数日收盘价序列图",

acf(Close.rtd,main='',xlab='Lag',ylab='ACF',las=1)    
title(main='(b) 上证指数收益率自相关检验',cex.main=0.95)

pacf(Close.rtd,main='',xlab='Lag',ylab='PACF',las=1)               
title(main='(c) 上证指数收益率偏自相关检验',cex.main=0.95)
def.off

## Q-Q图、经验累积分布ecdf图、密度图、直方图 
qqnorm(Close.rtd,main="(a) 上证指数收益率Q-Q图",cex.main=0.95,
       xlab='理论分位数',ylab='样本分位数')            
qqline(Close.rtd)                                 
#经验累积分布ecdf图
plot(ECD,lwd = 2,main="(b) 上证指数收益率累积分布函数图",cex.main=0.95,las=1) 
xx <- unique(sort(c(seq(-3, 2, length=24), knots(ECD))))         
abline(v = knots(ECD), lty=2, col='gray70')                           
x1 <- c((-4):3)             # 设定区间范围
lines(x1,pnorm(x1,mean(Close.rtdC[1:10]),sd(Close.rtd[1:10])))  
#密度图
plot(D, main="(c) 上证指数核密度曲线图 ",xlab="收益", ylab='密度',
     xlim = c(-7,7), ylim=c(0,0.5),cex.main=0.95)       
polygon(D, col="gray", border="black")                 
curve(dnorm,lty = 2, add = TRUE)                        

lines(x2,dnorm(x2,mean=0,sd=1))      
abline(v=0,lty = 3)                                     
legend("topright", legend=c("核密度","正态密度"),lty=c(1,2),cex=0.5)
#直方图
hist(Close.rtd[1:100],xaxt='n',main='(d) 上证指数收益率直方图',
     xlab='收益/100',ylab='密度', freq=F,cex.main=0.95,las=1)        
lines(x2,dnorm(x2,mean(Close.rtd[1:100]),sd(Close.rtd[1:100]))) 
axis(1,at=axTicks(1),labels = as.integer(axTicks(1))/100 )

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

点击标题查阅往期内容

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

【视频】随机波动率SV模型原理和Python对标普SP500股票指数预测|数据分享

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

左右滑动查看更多

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

SV模型

{
  N <- length(logReturn)
  mu <- (1/N)*sum(logReturn)
  sqrt((1/N) * sum((logReturn - mu)^2))
}

  return=-1.5*log(h)-y^2/(2*h)-(log(h)-mu)^2/(2*sigma2)
}

马尔可夫链蒙特卡罗估计

该模型使用了Kastner和Fruhwirth-Schnatter所描述的算法。使用的R代码是：

###Markov Chain Monte Carlo

summary(mcmc)

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

准最大似然估计

SV模型可以用QML方法在R中用许多不同的状态空间和Kalman滤波包来估计。

a0=c(parm[1])

  P0=matrix(parm[3]^2/(1-parm[2]^2))

  dt=matrix(parm[1]*(1-parm[2]))

  ct=matrix(-1.27)

  Tt=matrix(parm[2])

  Zt=matrix(1)

  HHt=matrix(parm[3]^2)

  GGt=matrix(pi^2/2)

  ans<-fkf(a0=sp$a0,P0=sp$P0,dt=sp$dt,ct=sp$ct,Tt=sp$Tt,Zt=sp$Zt,HHt=sp$HHt,GG

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列

正则化广义矩阵

在R函数中定义矩条件，然后估计参数0。

moments <- c (

    m1 = sqrt(2/pi)*exp(mu/2 + sig2h/8),

    m2 = exp(mu +  sig2h/2 ) ,

    m3 = 2*sqrt ( 2/pi ) * exp( 3*mu/2 + 9*sig2h/8 ) ,
    gmm(g = sv.moments , x =rets , t0=c(mu=-10, phi=0.9,sigmaeta= 0.2),

随机波动模型SV,马尔可夫蒙特卡罗法MCMC,正则化广义矩估计,准最大似然估计,上证指数收益时间序列