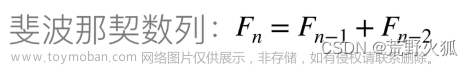我们一路奋战,
不是为了改变世界,
而是为了不让世界改变我们。

目录
我们一路奋战,
不是为了改变世界,
而是为了不让世界改变我们。
动态规划——DP算法(Dynamic Programing)
一、🏔斐波那契数列(递归VS动态规划)
1、🐒斐波那契数列——递归实现(python语言)——自顶向下
2、🐒斐波那契数列——动态规划实现(python语言)——自底向上
二、🏔动态规划算法——思想简介
1、🐒DP算法思想
2、🐒DP算法——解决问题的基本特征
3、🐒DP算法——解决问题的基本步骤
4、🐒求解例子——求阶乘 n!
三、🏔动态规划——常见例题
1、🐒求解最长不降子序列
2、🐒求解最长的公共子序列
获取源码?私信?关注?点赞?收藏?
动态规划——DP算法(Dynamic Programing)
一、🏔斐波那契数列(递归VS动态规划)

1、🐒斐波那契数列——递归实现(python语言)——自顶向下
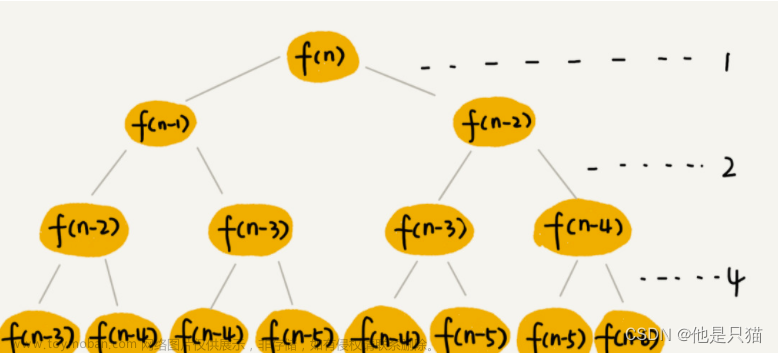
递归调用是非常耗费内存的,程序虽然简洁可是算法复杂度为O(2^n),当n很大时,程序运行很慢,甚至内存爆满。
def fib(n):
#终止条件,也就是递归出口
if n == 0 or n == 1:
return 1
else:
#递归条件
return (fib(n-1) + fib(n - 2))2、🐒斐波那契数列——动态规划实现(python语言)——自底向上
动态规划——将需要重复计算的问题保存起来,不需要下次重新计算。对于斐波那契数列,算法复杂度为O(n)。
def dp_fib(n):
#初始化一个数组,用于存储记录计算的结果。
res = [None] * (n + 1)
#前两项设置为1。
res[0] = res[1] = 1
#自底向上,将计算结果存入数组内。
for i in range(2, (n + 1)):
res[i] = res[i-1] + res[i-2]
return res[n]3、🐒方法概要
(1)构造一个公式,它表示一个问题的解是与它的子问题的解相关的公式:

(2)为这些子问题做索引,以便于它们能够在表中更好的存储与检索(用数组存储)。
(3)以自底向上的方法来填写这个表格;首先填写最小的子问题的解。
(4)这就保证了当我们解决一个特殊的子问题时,可以利用比它更小的所有可利用的子问题的解。
总之,因为在上世纪40年代(计算机普及很少时),这些规划设计是与“列表”方法相关的,因此被称为动态规划——Dynamic Programing。
二、🏔动态规划算法——思想简介
1、🐒DP算法思想
(1)将待求解的问题分解称若干个子问题,并存储子问题的解而避免计算重复的子问题,并由子问题的解得到原问题的解。
(2)动态规划算法通常用于求解具有某种最有性质的问题。
(3)动态规划算法的基本要素:最优子结构性质和重叠子问题。
最优子结构性质:问题的最优解包含着它的子问题的最优解。即不管前面的策略如何,此后的决策必须是基于当前状态(由上一次的决策产生)的最优决策。
重叠子问题:在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些问题被反复计算多次。对每个子问题只解一次,然后将其解保存起来,
以后再遇到同样的问题时就可以直接引用,不必重新求解。
2、🐒DP算法——解决问题的基本特征
(1)动态规划一般求解最值(最优、最大、最小、最长)问题;
(2)动态规划解决 的问题一般是离散的,可以分解的(划分阶段的)。
(3)动态规划结局的问题必须包含最优子结构,即可以有(n-1)的最优推导出n的最优。
3、🐒DP算法——解决问题的基本步骤
动态规划算法的四个步骤:
(1)刻画最优解的结构特性。(一维、二维、三维数组);
(2)递归的定义最优解。(状态转移方程)
(3)以自底向上的方法来计算最优解。
(4)从计算得到的解来构造一个最优解。
4、🐒求解例子——求阶乘 n!


#递归实现求阶乘
def multiply(n):
if n == 0 or n == 1:
return 1
return n * multiply(n -1)
#动态规划实现求阶乘
def dp_multiply(n):
temp = [None] * (n + 1)
temp[0] = 1
temp[1] = 1
for i in range(2, n + 1):
temp[i] = i * temp[i - 1]
return temp[n]三、🏔动态规划——常见例题
1、🐒求解最长不降子序列

(1)方法一:普通方法,算法复杂度为O(n^2)。
假设原始的数列为数组 a
分析:
刻画结构特性:用F[ i ] 表示前 i 项最长不下降子序列的长度;
状态转移方程:如果a [ i ] >=a [ j ], F[i] = max(F[i], F[j] + 1) 其中,0 <= j < i
数据存储:自底向上求解最小子结构最优解存入数组
其中,pre[ i ]表示以元素a [ i ] 为结尾的最长不降序列的前一个元素索引(也就是以a[i]结尾的最长不降序列的倒数第二个元素)。存储这个值是为了方便输出最长的不降序列。


def Longest_Increaseing(a):
F = [1] * len(a)
pre = [0] * len(a)
for i in range(1, len(a)):
for j in range(i):
if a[i] >= a[j]:
F[i] = max(F[i], F[j] + 1)
pre[i] = j
return F, pre
a = [5,2,8,6,3,6,9,7]
F, pre = Longest_Increaseing(a)
#这里只是能获得两个数组,其中F[i]的最大值就是最长不降序列的长度。接下来,输出最长的不降序列的元素值,请看下面的代码:
2、🐒求解最长的公共子序列








求解最长公共子序列代码如下(python语言):
import numpy as np
def LCS(str1, str2):
#获取两个序列的长度
m = len(str1)
n = len(str2)
#生成一个存储计算子问题的二位矩阵,并将元素初始化为0。
#这个矩阵的尺寸比两个序列的尺寸分别大1个单位。
#对于这个矩阵,第一行和第一列元素值必然为0。
#C[i][j]的含义是:Xi = (x1, x2, x3,..., xi)和Yj = (y1, y2, x3,..., yj)的最长公共子序列
C = np.zeros((m+1, n+1), dtype=int)
b = np.zeros((m+1, n+1), dtype=int)
for i in range(1, m+1):
for j in range(1, n+1):
#请注意这里为什么是i-1和j-1,因为其实C[1][1]表示的是
# 两个序列的首个元素的最长公共子序列,对应的是str1[0]和str2[0]
if str1[i-1] == str2[j-1]:
C[i][j] = C[i-1][j-1] + 1
b[i][j] = 1 #表示对角线方向
else:
if C[i][j-1] <= C[i-1][j]:
b[i][j] = 2 #表示朝上方向
else:
b[i][j] = 3 #表示朝左方向
C[i][j] = max(C[i][j-1], C[i-1][j])
return C, b
test1 = ['b', 'd','c', 'a', 'b', 'a']
test2 = ["a","b","c","b","d","a","b"]
a, b = LCS(test2, test1)
print(a)
#矩阵a存储的是公共子序列的长度,最大值就是最大公共子序列的长度
[[0 0 0 0 0 0 0]
[0 0 0 0 1 1 1]
[0 1 1 1 1 2 2]
[0 1 1 2 2 2 2]
[0 1 1 2 2 3 3]
[0 1 2 2 2 3 3]
[0 1 2 2 3 3 4]
[0 1 2 2 3 4 4]]
print(b)
#这里: 1表示对角线方向、2表示朝上、3表示朝左,主要是为了求具体的子序列用的。
[[0 0 0 0 0 0 0]
[0 2 2 2 1 3 1]
[0 1 3 3 2 1 3]
[0 2 2 1 3 2 2]
[0 1 2 2 2 1 3]
[0 2 1 2 2 2 2]
[0 2 2 2 1 2 1]
[0 1 2 2 2 1 2]]
接下来是输出最长公共子序列:
import numpy as np
def LCS(str1, str2):
#获取两个序列的长度
m = len(str1)
n = len(str2)
#生成一个存储计算子问题的二位矩阵,并将元素初始化为0。
#这个矩阵的尺寸比两个序列的尺寸分别大1个单位。
#对于这个矩阵,第一行和第一列元素值必然为0。
#C[i][j]的含义是:Xi = (x1, x2, x3,..., xi)和Yj = (y1, y2, x3,..., yj)的最长公共子序列
C = np.zeros((m+1, n+1), dtype=int)
b = np.zeros((m+1, n+1), dtype=int)
for i in range(1, m+1):
for j in range(1, n+1):
#请注意这里为什么是i-1和j-1,因为其实C[1][1]表示的是
# 两个序列的首个元素的最长公共子序列,对应的是str1[0]和str2[0]
if str1[i-1] == str2[j-1]:
C[i][j] = C[i-1][j-1] + 1
b[i][j] = 1 #表示对角线方向
else:
if C[i][j-1] <= C[i-1][j]:
b[i][j] = 2 #表示朝上方向
else:
b[i][j] = 3 #表示朝左方向
C[i][j] = max(C[i][j-1], C[i-1][j])
return C, b
def Print_Lcs(b, X, i , j):
if i == 0 or j == 0:
return
if b[i][j] == 1:
Print_Lcs(b, X, i-1, j-1)
print(X[i-1]) #为什么是i-1,因为b矩阵的行比X的行长一个单位,而且只输出相等的值,表示公共元素。
elif b[i][j] == 2:
Print_Lcs(b, X, i-1, j)
else:
Print_Lcs(b, X, i, j-1)
if __name__ == '__main__':
test1 = ['b', 'd','c', 'a', 'b', 'a']
test2 = ["a","b","c","b","d","a","b"]
a, b = LCS(test2, test1)
Print_Lcs(b, test2, 7, 6)
#输出的结果是: b、c、b、a 。(请注意这里结果不唯一,因为最长子序列长度为4, 存在三个序列长度为4的子序列)
好了,这篇博客到这就结束了,感谢大家的阅读!
2023年第二十九期,希望得到大家的喜欢🙇
也是新的系列,将会持续更新,🙇
希望大家有好的意见或者建议,欢迎私信
以上就是本篇文章的全部内容了
~ 关注我,点赞博文~ 每天带你涨知识!
1.看到这里了就 [点赞+好评+收藏] 三连 支持下吧,你的「点赞,好评,收藏」是我创作的动力。
2.关注我 ~ 每天带你学习 :各种前端插件、3D炫酷效果、图片展示、文字效果、以及整站模板 、HTML模板 、C++、数据结构、Python程序设计、Java程序设计、爬虫等! 「在这里有好多 开发者,一起探讨 前端 开发 知识,互相学习」!
3.以上内容技术相关问题可以相互学习,可 关 注 ↓公 Z 号 获取更多源码 !
获取源码?私信?关注?点赞?收藏?
👍+✏️+⭐️+🙇文章来源:https://www.toymoban.com/news/detail-691987.html
有需要源码的小伙伴可以 关注下方微信公众号 " Enovo开发工厂 "🙇文章来源地址https://www.toymoban.com/news/detail-691987.html
到了这里,关于Python—数据结构与算法---动态规划—DP算法(Dynamic Programing)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!