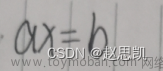目录
armadillo库功能介绍
armadillo库安装
vs中添加步骤
测试
armadillo库功能介绍
在c++编程中,我们在进行一些算法运算经常会面对矩阵计算,c++的标准库中是没有关于矩阵运算的库的,在面对矩阵计算我们只能自己编写相关代码进行计算,十分复杂,增加代码量,故出现了armadillo库,在armadillo库中我们只需输入armadillo库的相关函数,便可进行矩阵运算。(armadillo函数大部分等同于matlab中的矩阵函数。在安装包中也有对应的PDF进行功能介绍)
armadillo库安装
安装环境:vs2013
安装链接(百度云)
链接:https://pan.baidu.com/s/1yvXpqq6XTQLxQTtmqxqS8Q
提取码:vrvy
解压压缩包

vs中添加步骤
1.解压压缩包后打开vs,新建项目,点击生成,配置管理器,将平台改为x64


2. 打开项目属性页,在vc++目录内,将包含目录->编辑->添加解压后的include文件夹的路径


注意:是添加includ文件夹的路径!

提示:下图界面内地址

文章来源地址https://www.toymoban.com/news/detail-692217.html
3.库目录编辑->添加examples文件夹下lib_win64文件夹的路径(提示:下图界面的文件地址)

4.在C/C++中,附加包含目录->编辑->添加include文件路径

5.点击链接器->常规->附加库目录->编辑->添加examples下lib_win64路径

6.选择链接器->输入,将附加依赖项里添加exmples中lib_win64文件夹内两个lib文件


7.点击确定,推出配置,点击重新生成解决方案

8.将examples中lib_win64的两个.dll文件复制到新建项目的x64,debug下

测试
最后测试代码,在examples下exmple1.cpp内代码复制到新建的cpp项目下,运行程序

测试成功,安装结束
文章来源:https://www.toymoban.com/news/detail-692217.html
到了这里,关于armadillo库安装教程的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!