OFDM多径传输时域和频域模型，以及循环前缀的作用-Toy模板网

这篇具有很好参考价值的文章主要介绍了OFDM多径传输时域和频域模型，以及循环前缀的作用。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

文章来源地址https://www.toymoban.com/news/detail-693355.html

1、多径信道传输模型

从信号传输的基本模型入手。考虑如下式所示的线性时不变系统，
$\int h(\tau) x(t- \tau) d\tau = \int h(t-\tau) x(\tau) d\tau \quad \quad (1)$

其中， $x (t)$ 表示输入信号， $h (t)$ 表示信道冲激响应， $y (t)$ 表示接收信号。则离散形式为
$\sum_{l=0}^{L-1} h(l) x(n-l) \quad \quad (2)$

式（2）是多径信道下的信号传输模型。 $L$ 表示多径信道的阶数。

2、OFDM循环前缀的作用

对于OFDM来说，发射信号 $x (n)$ 由IFFT运算（有效信号）和添加循环前缀（CP）得到，其中有效信号可以表示为
$\frac{1}{\sqrt{N}} \sum_{k=1}^{N} X(k) e^{j 2\pi \frac{nk}{N}}, n=1, \ldots, N, k = 1, \ldots, N \quad \quad (3)$

式中， $X (k)$ 为第 $k$ 个子载波上的发射信号， $N$ 为IFFT的点数（也是一个OFDM符号时域有效信号 $x (n)$ 的样点数目)。

对于单个OFDM符号，接收信号（2）的矩阵形式如下：
$\begin{bmatrix} y(-N_{CP}) \\ \vdots \\ y(-1) \\ y(0) \\ y(1) \\ y(2) \\ \vdots \\ y(N-2) \\ y(N-1) \end{bmatrix} = \begin{bmatrix} h(0)& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \vdots & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ h(L-1) & \cdots & h(0) & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & h(L-1) & \cdots & h(0) & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \ddots & \vdots & h(0) & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & h(L-1) & & h(0) & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \ddots & & \ddots & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \ddots & & h(0) & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & h(L-1) & \cdots & h(0) \end{bmatrix} \begin{bmatrix} x(-N_{CP}) \\ \vdots \\ x(-1) \\ x(0) \\ x(1) \\ x(2) \\ \vdots \\ x(N-2) \\ x(N-1) \end{bmatrix} \quad \quad (4)$

式中， $N_{CP}$ 表示CP的长度。

CP的第一个作用：避免符号间干扰。 由于多径的作用，前一时刻的信号会对当前时刻的信号造成影响。因此，为了保证上一个OFDM不会对当前OFDM符号造成影响，CP的长度必须满足 $N_{CP} \geq L-1$ 。在式（4）中， $N_{CP} = L$ 。

CP的第二个作用：消除子载波间干扰。 这一部分不容易直观理解，需要经过一部分推导。

3、CP如何消除子载波间干扰

为了说明这个问题，继续观察式（4）。从CP的定义出发，循环前缀指的是将发射信号的后面一部分信号复制，并添加到前面，即 $\ldots, x(-N_{CP}) = x(N-N_{CP})$ 。在接收端去除CP，并利用这个性质，可以将式（4）表示为
$\begin{bmatrix} y(0) \\ y(1) \\ y(2) \\ \vdots \\ y(N-2) \\ y(N-1) \end{bmatrix} = \begin{bmatrix} 0 & h(L-1) & \cdots & h(0) & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \ddots & \vdots & h(0) & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & h(L-1) & & h(0) & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \ddots & & \ddots & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \ddots & & h(0) & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & h(L-1) & \cdots & h(0) \end{bmatrix} \begin{bmatrix} x(-N_{CP}) \\ \vdots \\ x(-1) \\ x(0) \\ x(1) \\ x(2) \\ \vdots \\ x(N-2) \\ x(N-1) \end{bmatrix} \quad \quad (5)$
$\begin{bmatrix} y(0) \\ y(1) \\ y(2) \\ \vdots \\ y(N-2) \\ y(N-1) \end{bmatrix} = \begin{bmatrix} h(0) & 0 & 0 & 0 & h(L-1) & h(1) \\ \vdots & h(0) & 0 & 0 & 0 & h(L-1) \\ h(L-1) & & h(0) & 0 & 0 & 0 \\ 0 & \ddots & & \ddots & 0 & 0 \\ 0 & 0 & \ddots & & h(0) & 0 \\ 0 & 0 & 0 & h(L-1) & \cdots & h(0) \end{bmatrix} \begin{bmatrix} x(0) \\ x(1) \\ x(2) \\ \vdots \\ x(N-2) \\ x(N-1) \end{bmatrix} \quad \quad (6)$

也就是说，由于CP性质，可以将式（5）中信道矩阵的左上角元素，搬移到式（6）中信道矩阵的右上角，且完全不会改变等号的成立。即，CP-OFDM将线性卷积运算转换为了循环卷积运算。

将（6）写为矩阵形式，即
$\mathbf{y} = \mathbf{G} \mathbf{x} \quad \quad (7)$

其中， $\mathbf{G} \in \mathbb{C}^{N \times N}$ 为时域信道矩阵。根据OFDM接收端的操作，需要对接收信号进行FFT运算，可以得到频域信号形式，即
$\mathbf{r} = \mathbf{F} \mathbf{y} = \mathbf{F} \mathbf{G} \mathbf{F}^{H} \mathbf{s} \quad \quad (8)$

式中， $\mathbf{F} \in \mathbb{C}^{N \times N}$ 表示傅里叶矩阵， $\mathbf{s} = [X(1), \ldots, X(k), \ldots, X(N)]^{T} \in \mathbb{C}^{N \times 1}$ 表示频域发射信号（见式（3））。

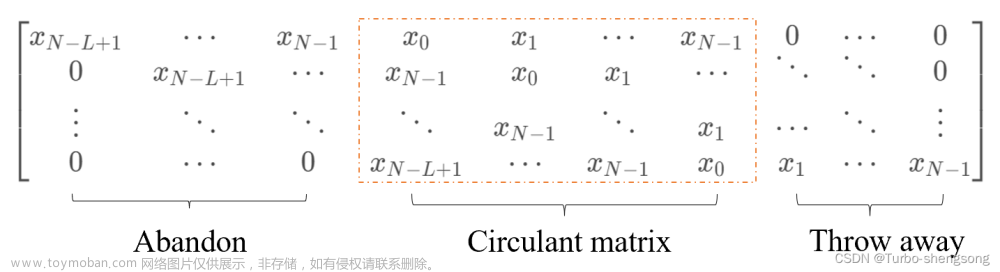
注意： 式（7）中 $\mathbf{G}$ 是一个Toeplitz矩阵，具有循环移位特性，如下图所示。
ofdm循环前缀,算法
定义 $\mathbf{H} = \mathbf{F} \mathbf{G} \mathbf{F}^{H}$ ，利用托普利兹矩阵_百度百科的性质，则 $\mathbf{H}$ 是一个对角矩阵，式（8）可以表示为
$\begin{bmatrix} r(0) \\ r(1) \\ r(2) \\ \vdots \\ r(N-1) \end{bmatrix} = \begin{bmatrix} H(0) & & & & \\ & \ddots & & & \\ & & H(k) & & \\ & & & \ddots & \\ & & & & H(N-1) \end{bmatrix}\begin{bmatrix} X(0) \\ \vdots \\ X(k) \\ \vdots \\ X(N-1) \end{bmatrix} \quad \quad (9)$

式中， $H (k)$ 表示 $\mathbf{H}$ 的第 $k$ 个对角线元素。从式（9）可以看到，每一个子载波的接收信号与发射信号一一对应，且其他子载波的信号对当前子载波完全没有影响。也就是说，子载波之间不会产生任何干扰，即消除了子载波间干扰。OFDM结合循环前缀，可以使信道均衡、信号解调等在频域并行处理，大大降低了系统复杂度。

此外，上面的过程解释了OFDM时域传输模型以及频域传输模型的等价关系。

4、OFDM频域与时域信道系数的关系

现在还有一个问题，如何确定频域信道系数 $H (k)$ 与时域信道系数 $h (l)$ 之间的关系呢？

为了解决这个问题，考察特征值和特征向量。

根据 $\mathbf{H} = \mathbf{F} \mathbf{G} \mathbf{F}^{H}$ ，可知 $H (k)$ 是Toeplitz矩阵 $\mathbf{G}$ 的特征值，相应的特征向量为 $\mathbf{F}^{H}$ 的第 $k$ 列。为什么呢？因为 $\mathbf{F}^{H} \mathbf{H} = \mathbf{G} \mathbf{F}^{H}$ 。
考虑矩阵两边的第 $k$ 个列向量，可得 $\mathbf{G} \mathbf{f}_{k} = H(k) \mathbf{f}_{k}$ ，其中 $\mathbf{f}_{k}$ 是 $\mathbf{F}^{H}$ 的第 $k$ 列，也就是 $\mathbf{F}$ 的第 $k$ 行。这与特征值和特征向量的表达式完全相同。基于以上讨论，我们下面来说明如何计算 $H (k)$ 。

定义： $W_{N} = e^{-\frac{j 2\pi}{N}}$ ，以及 $\mathbf{G} \mathbf{f}_{k} = H(k) \mathbf{f}_{k}$ 的等价形式，即
$\frac{1}{\sqrt{N}} \begin{bmatrix} p_{0} & p_{1} & p_{2} & \cdots & p_{N-1} \\ p_{N-1} & p_{0} & p_{1} & \cdots & p_{N-2} \\ p_{N-2} & p_{N-1} & p_{0} & \cdots & p_{N-3} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ p_{1} & p_{2} & p_{3} & \cdots & p_{0} \end{bmatrix} \begin{bmatrix} W_{N}^{0} \\ W_{N}^{-k} \\ W_{N}^{-2k} \\ \vdots \\ W_{N}^{-(N-1)k} \end{bmatrix} = \frac{1}{\sqrt{N}} H(k) \begin{bmatrix} W_{N}^{0} \\ W_{N}^{-k} \\ W_{N}^{-2k} \\ \vdots \\ W_{N}^{-(N-1)k} \end{bmatrix} \quad \quad \quad (10)$

为了计算 $H (k)$ 的表达式，我们观察式（6）和（10）中的Toeplitz矩阵 $\mathbf{G}$ 和 $\mathbf{P}$ ，
有 $\mathbf{P}_{m,n} = p_{(n-m) \text{mod} N}$ ， $p_{l} = h_{(N-l) \text{mod} N}$ ，其中 $\ldots, N-1.$ 。
因此，式（10）等号左边：矩阵 $\mathbf{P}$ 的第 $(m + 1)$ 行与IDFT矩阵第 $k$ 列的内积有
$\frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} p_{(n-m)_N} W_{N}^{-nk} = \frac{1}{\sqrt{N}} W_{N}^{-mk} \sum_{n=0}^{N-1} p_{(n-m)_N} W_{N}^{-(n-m)_{N}k} = \frac{1}{\sqrt{N}} W_{N}^{-mk} \sum_{l=0}^{N-1} p_{l} W_{N}^{- l k} \quad \quad (11)$

式中，第1个等号利用了性质 $W_{N}^{-(n-m)k} = W_{N}^{-(n-m)_{N} k}$ ，（以 $N$ 为周期的周期性）。
为进一步计算式（11）的求和项，我们定义 $H_{k} = \sum_{l=0}^{N-1} p_{l} W_{N}^{- l k}$ ，即
$H_{k} = \sum_{l=0}^{N-1} p_{l} W_{N}^{- l k} = \sum_{l=0}^{N-1} h_{(N-l)_{N}} W_{N}^{- l k} = \sum_{l=0}^{N-1} h_{(N-l)_{N}} W_{N}^{(N - l)_{N} k} = \sum_{l'=0}^{N-1} h_{l'} W_{N}^{l' k} \quad \quad (12)$

式中，第3个等号利用了性质 $W_{N}^{N k} = 1$ ， $W_{N}^{(N - l) k} = W_{N}^{(N - l)_{N} k}$ 。
可以看到，频域信道系数 $H_{k}$ 恰巧是时域信道系数 $h_{l'}, l' = 0,1,\ldots,N-1$ 的傅里叶变换！
（注意 $L,\ldots, N-1$ 时 $h_{l'} = 0$ ），上式可以进一步表示为 $H_{k} = \sum_{l=0}^{L-1} h_{l} e^{-\frac{j 2\pi }{N}l k}$ 。

因此，我们可以得出公式（9）中，频域信道系数与时域信道系数之间的关系，以及验证了时域传输模型（6）和频域传输模型（9）之间的等价性。

参考资料：
CP是如何将多径信道的线性卷积变成循环卷积的？_张力_通信之美_新浪博客
https://blog.51cto.com/u_15127585/2669966
OFDM系统中的信道估计基础知识_逸凌Time的博客-CSDN博客_ofdm信道估计
给“小白”图示讲解OFDM的原理_码懂的博客-CSDN博客_ofdm小白
OFDM系统中的信道估计基础知识_逸凌Time的博客-CSDN博客_ofdm信道估计

到了这里，关于OFDM多径传输时域和频域模型，以及循环前缀的作用的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！