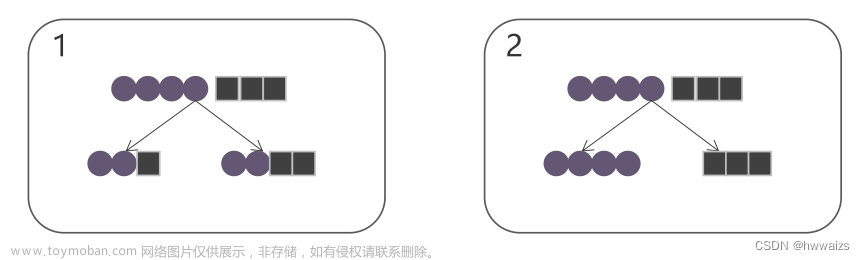
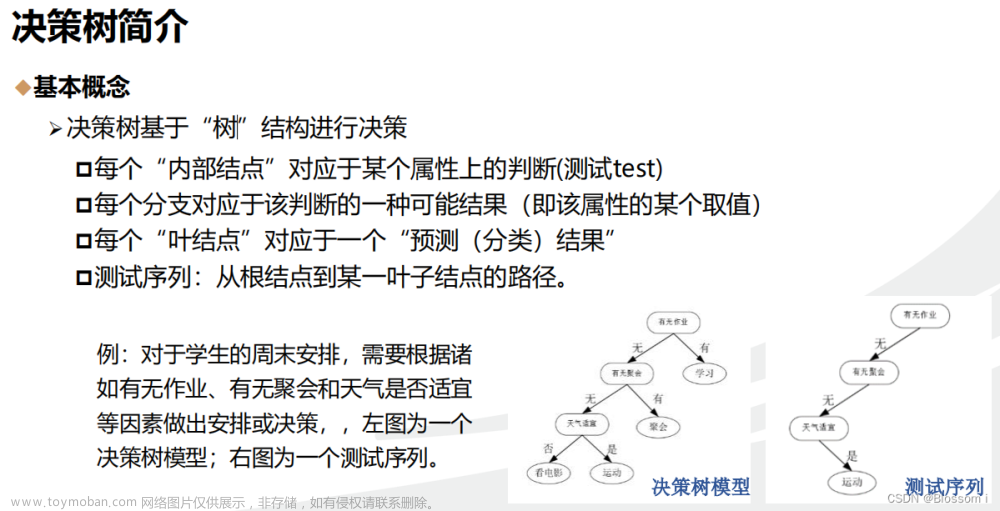
1.信息增益和基尼系数的异同点
信息增益和基尼系数都是用于评价决策树分裂节点的指标,它们有以下主要的相同点和不同点:
相同点:
- 都用于测度数据集的无序程度(impurity),可以评价分裂后的无序程度减少量
- 取值范围都在0到1之间,0表示完全有序
- 都遵循同一思路,优先选择造成无序程度最大减少的特征进行分裂
不同点:
- 计算方式不同
- 信息增益基于香农熵,衡量分裂前后信息的变化量
- 基尼系数基于数据集标记的概率分布,衡量分裂前后不确定性变化量
- 信息增益更倾向选择取值较多的特征
- 基尼系数在小数据集上表现更稳定
综合来说,两者都可以有效指导决策树的特征选择,但计算和偏好上有一定差异。需要根据数据集和问题领域选择合适的指标。一般来说,分类问题使用信息增益,回归问题使用基尼系数的情况较多。
2.如何判断是使用的信息增益还是基尼指数
决策树在选择特征时使用的指标,决定使用信息增益还是基尼系数主要取决于以下两个因素:
算法实现
不同的决策树算法实现会有默认的指标选择。例如:
- scikit-learn中的DecisionTreeClassifier默认使用基尼系数
- CART算法通常默认使用基尼系数
- ID3算法默认使用信息增益
- 需要查看具体的算法实现来确认默认使用的是哪个指标。
参数设定
一些算法实现同时支持信息增益和基尼系数两种指标,可以通过参数进行设定。
例如scikit-learn中的DecisionTreeClassifier,可以通过criterion参数设定:
- criterion='gini' 使用基尼系数
- criterion='entropy' 使用信息增益
所以综合以上两点,可以查看算法的具体实现,以及参数配置,来判断该算法是否使用信息增益或基尼系数作为划分特征的评价指标。大多数实现会有默认的指标,也支持通过参数进行修改。理解算法的原理可以帮助我们做出正确的判断。
3.各个算法的默认参数
常见的几种决策树算法的参数默认使用的特征划分指标如下:
- ID3算法:默认使用信息增益(information gain)
- C4.5算法:默认使用信息增益
- CART算法:默认使用基尼系数(Gini impurity)
- Scikit-Learn的DecisionTreeClassifier:默认使用基尼系数
- Scikit-Learn的DecisionTreeRegressor:默认使用均方差(mean squared error)
- Spark MLlib的DecisionTree:默认使用基尼系数
- XGBoost: 默认使用基尼系数
- LightGBM: 默认使用基尼系数
所以信息增益更多地在ID3、C4.5中被作为默认指标。
而基尼系数被更多地应用于CART、Scikit-Learn中的决策树,以及集成算法(随机森林、GBDT等)中。
当然,许多算法实现也提供了通过参数修改指标的功能。
正确理解并配置算法的参数,可以帮助我们构建出有效的决策树模型。
4.与默认指标不同的设定
LightGBM也可以使用信息增益作为决策树划分的指标。
LightGBM默认使用基尼系数来选择划分特征,但也提供了使用信息增益的功能选项。
具体来说,在LightGBM的算法参数中,有一个名为"metric"的参数,它决定了评价特征划分的指标。默认值为"None",表示使用基尼系数。
如果设置metric='entropy',则会使用信息增益来选择特征,所以虽然此时假如不设定具体的参数会默认使用基尼指数来进行特征划分,但是也可以通过修改参数来使用信息增益进行特征选择。
import lightgbm as lgb
params = {'metric': 'entropy'}
model = lgb.train(params, lgb_dataset)所以您看到的LightGBM使用信息增益(entropy),很可能是通过指定了这个metric参数来实现的。
尽管默认是基尼系数,但LightGBM提供了灵活的指标选择,我们可以根据问题需要进行配置。
5.根据不同的情况选择特征
在决策树算法中,根据不同的情况选择使用信息增益或基尼系数的一些经验准则如下:文章来源:https://www.toymoban.com/news/detail-693935.html
- 分类问题更倾向使用信息增益,回归问题更倾向使用基尼系数。
- 如果特征取值范围差异很大,信息增益更适合,因为它偏向选择取值范围广的特征。
- 如果样本量少于50,基尼系数表现更稳定。
- 类别不均衡的数据集建议使用信息增益,因为基尼系数容易偏向主要类别。
- 需要快速构建模型,基尼系数计算上更有优势。
- 对训练时间敏感的大数据集,基尼系数更高效。
- 喜好树的结构简单的情况,基尼系数可能更合适。
- 想要获得可解释性强的树,信息增益更适合。
总结一下,信息增益偏向分类问题,基尼系数偏向回归;信息增益适用于取值范围差异大和类别不均衡的数据;基尼系数在小样本和大数据集上表现更好。可以根据数据集统计特点和问题需求进行选择。也可以尝试两者,看分类准确率或回归效果哪个指标更优。文章来源地址https://www.toymoban.com/news/detail-693935.html
importances = svr.coef_
sorted_idx = np.argsort(np.abs(importances))[::-1]到了这里,关于importance中信息增益和基尼系数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!