Propositional SAT Solving：DPLL算法求解CNF SAT 与 数独求解程序(C++ 实现)

Ⅰ、前置知识

1. 文字（literal）：原子命题及其否定称为文字。其可以使用布尔变量进行表示，其值为真 或 假。e.g. $literalp,r,q和\neg p,\neg r,\neg q$ 其都是文字

2. 子句（clause） 子句可以是简单析取式：仅由有限个文字构成的析取式称为子句或简单析取式。e.g.$p\vee q\vee \neg r$ 即为一个子句。

3. 合取范式（Conjunctive Normal Form, CNF）：仅由有限个简单析取式构成的合取式称为合取范式。e.g. $(-x1\vee -x2\vee x3)\wedge (-x3\vee x4)$

对于三者的关系，Handbook of Model Checking 给出的定义为：
A literal is a variable x or its complement ¬x，A clause c is a non-tautologous disjunction of literals，A CNF formula F is a conjunction of clauses.
翻译为，literal 为一个 变量 或者 它的非；clause 是非同义的 多个 literal 的析取；一个 CNF 公式为多个子句的合取。

可满足性问题（Satisfiability） 是用来解决给定的真值方程式，是否存在一组变量赋值，使问题为可满足。布尔可满足性问题（Boolean satisfiability problem SAT）属于决定性问题，也是第一个被证明属于NP完全的问题。

• 有的问题无法通过直接的算式计算（比如质因数分解）得到，只能通过间接的猜算来得到结果，这就是非确定性问题。
• 而且可以告知你"猜算"的答案正确与否的算法，假如其可以在多项式时间内算出来，其就是NP问题。
• 如果这个问题的所有可能答案，都可以在多项式的时间内进行正确与否的演算，即（Non-deterministic Polynomial Complete）NPC问题。

Ⅱ、算法介绍

DPLL（Davis-Putnam-Logemann-Loveland）算法，是一种完备的、以回溯为基础的算法，用于解决在合取范式（CNF）中命题逻辑的布尔可满足性问题；也就是解决CNF-SAT问题。

DPLL算法是一种搜索算法，思想与DFS十分相似，其类似于上述我们设想的“暴力”算法：搜索所有可能的赋值排列。

算法思想

简单地讲，算法会在公式中选择一个变量（literal），将其赋值为True，化简赋值后的公式，如果简化的公式是可满足的（递归地判断），那么原公式也是可满足的。否则就反过来将该变量赋值为False，再执行一遍递归的判定，若也不能满足，那么原公式便是不可满足的，回溯回到上一个可以排定为真的情况，继续选择下一个变量。

根据上述思想，在最坏的情况下，其回溯会导致一次复杂度为指数时间的计算。而为了避免这种情况，DPLL引入了单位传播。

单位传播

单位传播（Unit Propagation）UP 或 布尔约束传播（Boolean Constraint Propagation, BCP）是一个能够简化合取范式的方法。

定义 单位子句（unit clause） 为只有一个文字的子句，例如 $p或者\neg p$。如果一个CNF为真，则在其每个子句内，至少有一个变量为真。假如出现了单位子句的情况，而单位子句又只有一个变量，所以这个变量也必须为真。如果一个合取范式包含一个单位子句$p$，那么该CNF中的其他子句就可以被$p$化简。具体做法如下：

1. 如果某个子句中含有$p$，那么就把这个子句移除。因为此时这个子句已经为真了，其他变量的取值已经不重要。e.g.
   $$((p\vee q\vee r)\wedge (x\vee y)\wedge r)$$如上面的式子，有单位子句r，则 r 的值一定为 真 ，则CNF的第一个子句也必须为真。经过UP得到$$((x\vee y)\wedge r)$$
2. 如果某个子句中含有$\neg p$，那么就把这个子句中的$\neg p$ 移除。因为这个子句如果为真，其取值已经不取决于$\neg p$，因此删掉。
   $$((p\vee q\vee \neg r)\wedge (x\vee \neg r)\wedge r)$$如上面的式子，有单位子句r，则 r 的值一定为 真 ，则CNF的第一个子句中的 非r 不影响其子句为真的情况，可以移除，同理对第二个子句进行同样的操作。经过UP得到$$((p\vee q)\wedge x\wedge r)$$

伪代码和实现

DPLL是一种基于回溯的算法，其核心就是单位传播（CDCL也是如此，CDCL 对于算法的升级不在此处）。一个朴素的回溯算法可能会尝试每种可能的赋值，直到找到一组成真赋值为止。而DPLL可以利用单位传播来进行“更聪明”的猜测，从而减小搜索树的大小（可以将单位传播看成一种剪枝策略）。将 指数级的复杂度 简化成了 多项式。

在尝试进行赋值（猜测）时，也可以对其进行优化，朴素的回溯算法是按顺序对出现的变量进行赋值，我们可以对变量出现的次数进行排序，每次赋值时都将出现次数最大的变量首先赋值，这样影响到的子句更多，更有可能回出现单位子句。

在求解的过程中，如果我们发现某个子句的真值为真，就删除这个子句；如果发现某个文字的真值为假，就在子句中删除这个变量。

这样，最后发现CNF为空，就说明所有子句都满足了，即该CNF是可满足的；如果发现CNF中有一个子句为空，则表示了此次赋值尝试是失败的。如果每次赋值（即猜测）都出现了这种情况，那么该CNF就是不可满足的。

伪代码：

DPLL(CNF):
  对CNF进行单元传播.
  if: CNF为空, return True.
  if: CNF存在空子句, return False.
  else :
  	选择下一个进行赋值（猜测）的变量
    Return DPLL(with that variable True) || DPLL(with that variable False)

部分关键代码：

int SATSolverDPLL::unit_propagation(Formula &f) {//单元传播
  bool unit_clause_found = false;
  if (f.clauses.size() == 0) {
    return Cat::satisfied;
  }
  do {
    unit_clause_found = false;
    for (int i = 0; i < f.clauses.size(); ++i) {
      if (f.clauses[i].size() == 1) {//其子句的长度为1 则其为单元子句
        unit_clause_found = true;
        f.literals[f.clauses[i][0] / 2] = f.clauses[i][0] % 2;
        //0 - if true, 1 - if false, set the literal
        f.literals_frequency[f.clauses[i][0] / 2] = -1;
        int result = apply_transform(f, f.clauses[i][0] / 2);//进行传播
        if (result == Cat::satisfied or result == Cat::unsatisfied) {
          return result;
        }
        break;
      } else if (f.clauses[i].size() == 0) {
        return Cat::unsatisfied;
      }
    }
  } while (unit_clause_found);
  return Cat::normal;
}

int SATSolverDPLL::DPLL(Formula f) {
  int result = unit_propagation(f);//进行单元传播
  if (result == Cat::satisfied) {
    if (type == 1) {
      show_result1(f, result);
    } else if (type == 2) {
      show_result2(f, result);
    }
    return Cat::completed;
  } else if (result == Cat::unsatisfied) {
    return Cat::normal;
  }
  int i = distance(f.literals_frequency.begin(), max_element(f.literals_frequency.begin(), f.literals_frequency.end()));
  // 找到出现次数最多的变量 
  for (int j = 0; j < 2; ++j) {
    Formula new_f = f;
    if (new_f.literal_polarity[i] > 0) {//此处考虑了出现变量的正负，选定的变量如果正的多，先猜测 其为 p，反之 再猜测其值为 非p。
      new_f.literals[i] = j;
    } else {
      new_f.literals[i] = (j + 1) % 2;
    }
    new_f.literals_frequency[i] = -1;
    // reset the frequency to -1 to ignore in the future
    int transform_result = apply_transform(new_f, i);
    if (transform_result == Cat::satisfied) {
      if (type == 1) {
        show_result1(new_f, transform_result);
      } else if (type == 2) {
        show_result2(new_f, transform_result);
      }
      return Cat::completed;
    } else if (transform_result == Cat::unsatisfied) {
      continue;
    }
    int dpll_result = DPLL(new_f);
    if (dpll_result == Cat::completed) {
      return dpll_result;
    }
  }
  return Cat::normal;
}

运行结果如图所示，输入的例子即为下面网址中的一个，
$$\begin{gathered} C1=\neg x2\vee \neg x3\vee \neg x4\vee x5 \\ C2=\neg x1\vee \neg x5\vee x6 \\ C3=\neg x5\vee x7 \\ C4=\neg x1\vee \neg x6\vee \neg x7 \\ C5=\neg x1\vee \neg x2\vee x5 \\ C6=\neg x1\vee \neg x3\vee x5 \\ C7=\neg x1\vee \neg x4\vee x5 \\ C8=\neg x1\vee x2\vee x3\vee x4\vee x5\vee \neg x6 \\ f=C1\wedge C2\wedge C3\wedge C4\wedge C5\wedge C6\wedge C7\wedge C8\wedge \end{gathered}$$输入的CNF 有7个变量，8个子句。
最终的结果为第一个变量为 false，第5 ， 7 个变量必须为true 其余随意。

对算法的理论部分已经介绍完毕，为加深其理解可以看这个University of Washington | CSE 442。其中有该算法和 其升级版的CDCL的可视化交互操作与讲解，更加便于理解。

Ⅲ、应用于数独

lz也是在阅读了上面的讲解后，加深了理解。开篇有个例子，就是数独，其也是NPC问题，便希望将数独用 CDLL 算法求解出来。再阅读了多篇GitHub后，写出了自己的代码，并且自认为其是正确的解法（为什么是自认为，因为在GitHub上我用心去看的都是错误的。。。有小bug，也有理解就出现错误的，所以说，如果我错了，希望各位可以dd我，指正我）。

生成数独

首先是生成合法的9×9数独，对于需要求解的问题数独将已经生成的合法的数独挖去几个方块，就生成了数独问题。

那么生成数独的策略即为先随机生成第一行，再根据数独的要求一个个填充剩下的9×9方格的空缺。数独的合法性要求如下：

1. 行不能出现重复的数字
2. 列不能出现重复的数字
3. 在3×3的子方格中也不能出现重复的数字

实现代码

#include "Global.h"
using namespace std;

void ShowProblem(int a[][9]) {
  for (int i = 0; i < 9; ++i) {
    for (int j = 0; j < 9; ++j) {
      if (a[i][j] != 0) {
        printf("%d ", a[i][j]);
      } else {
        printf("_ ");
      }
    }
    printf("\n");
  }
}
void GenerateFirstLine(int a[]) {
  srand((unsigned) time(NULL));//设置随机数种子为 真随机 数 in English  set it for true random number
  for (int i = 0; i < 9; ++i) {
    a[i] = rand() % 9 + 1;
    int j = 0;
    while (j < i) {
      if (a[i] == a[j]) {
        a[i] = rand() % 9 + 1; //生成随机的不同的9个数字 in English generate nine random number
        j = 0;
      } else {
        j++;
      }
    }
  }
}

int CompleteSudoku(int a[][9], int x, int y) {
  if (x < 9 and y < 9) {
    int check[10];//用来表示没使用过的 即合法的 数字。0 合法 1 非法 in English: 0 is legal , 1 is illegal
    memset(check, 0, sizeof(check));
    for (int i = 0; i < y; ++i) {
      check[a[x][i]] = 1; //在第 x 行出现的数字 非法
    }
    for (int i = 0; i < x; ++i) {
      check[a[i][y]] = 1;// 在第 y 列出现的数字 非法
    }
    //在 x,y处出现的值，不能在其3×3 的小方格内出现
    for (int i = x / 3 * 3; i < x / 3 * 3 + 3; ++i) {
      for (int j = y / 3 * 3; j < y / 3 * 3 + 3; ++j) {
        if (i == x or j == y) {
          continue;
        }
        check[a[i][j]] = 1;
      }
    }
    int fl = 0;
    for (int i = 1; i <= 9 and fl == 0; ++i) {
      //从 check 中合法的值开始一个个选取
      if (check[i] == 0) {
        fl = 1;
        a[x][y] = i;
        if (y == 8 and x != 8) {
          //所选方格的赋值到了最后一列 就向下一行的第一个移动
          if (CompleteSudoku(a, x + 1, 0) == 0) {
            return 0;
          } else {
            fl = 0;
          }
        } else if (y != 8) {
          //即 如果所选方格没在最后一列时，向后移动即可
          if (CompleteSudoku(a, x, y + 1) == 0) {
            return 0;
          } else {
            fl = 0;
          }
        }
      }
    }
    if (fl == 0) {
      a[x][y] = 0;
      return 1;
    }
  }
  return 0;
}

void CreateSudoku(int a[][9]) {
  GenerateFirstLine(a[0]);
  CompleteSudoku(a, 1, 0);
}

void CreateProle(int a[][9], int b[][9], int empty_number) {
  // a 为原来完整的数独，b 为我们需要的数独问题 in English : a is the sudoku we want to generate b is the sudoku problem
  srand((unsigned) time(NULL));//设置随机数种子为 真随机 数
  for (int i = 0; i < 9; ++i) {
    for (int j = 0; j < 9; ++j) {
      b[i][j] = a[i][j];
    }
  }
  for (int i = 0; i < empty_number; ++i) {
    int x = rand() % 9;
    int y = rand() % 9;

    if (b[x][y] != 0) {
      b[x][y] = 0;
    } else {
      i--;
    }
  }
}

void CreateSudokuProblem(int empty_number) {
  int sudoku[9][9] = {0};// the sudoku we want to generate
  int sudoku_backup[9][9] = {0};// the sudoku problem we want to generate
  CreateSudoku(sudoku);
  CreateProle(sudoku, sudoku_backup, empty_number);
  ShowProblem(sudoku_backup);
  string path = "..\\sudoku.cnf";
  Sudoku2CNF(path, sudoku_backup, empty_number);
}

数独 to CNF

生成数独后，由于我们的SAT Solver只能处理CNF，因此如何将数独转化成CNF才是这个问题中最困难的点。

首先我们需要确立变量的表示， $X_{111}^{}$为一个变量，表示第一行第一列的方块的值为1，那么同理$X_{558}^{}$表示第5行第5列的方块的值为8。

有了数独如何表示成变量后，那么构建CNF的规则如何制定呢。上述华盛顿大学的文章中，在末尾处其实已经提到了。其也就是我们生成数独时需要遵守的规则。

现在让我用专业的逻辑表达式来表示4条规则（第四条规则可能表达不太对，思想下面会解释）
$$\begin{array}{l}1.{\bigwedge }_{x=1}^9{\bigwedge }_{y=1}^9{\bigvee }_{z=1}^9{s}_{xyz}\\ 2.{\bigwedge }_{y=1}^9{\bigwedge }_{z=1}^9{\bigwedge }_{x=1}^8{\bigwedge }_{i=x+1}^9\left(\neg s_{xyz}\vee \neg s_{iyz}\right)\\ 3.{\bigwedge }_{x=1}^9{\bigwedge }_{z=1}^9{\bigwedge }_{y=1}^8{\bigwedge }_{i=y+1}^9\left(\neg s_{xyz}\vee \neg s_{xiz}\right)\\ 4.{\bigwedge }_{z=1}^9{\bigwedge }_{i=0}^2{\bigwedge }_{j=0}^2{\bigwedge }_{x=1}^3{\bigwedge }_{y=1}^3{\bigwedge }_{k=1}^{3,k\ne x}{\bigwedge }_{l=1}^{3,l\ne y}\left(\neg s_{(3i+x)(3j+y)z}\vee \neg s_{(3i+k)(3j+l)z}\right)\end{array}$$

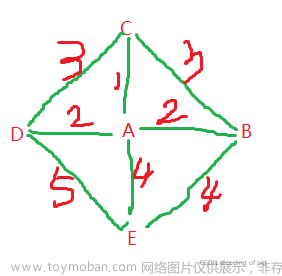
对于以上4条规则，其分别代表了每个方块只有一个取值，行不能重复，列不能重复和每个3×3的子方块不能重复这四条规则。可能最后一条规则不是很好理解，我用图的方式表示。

最后一条规则，表示了1-9的z的取值中，我们行有0-2的i ，列有0-2的j
共9 子3×3的方块，在每个方块中行有1-3的x ，列有1-3的y共9 子1×1的方块。而 k 和 l 则表示其不能和我们选中的方块在同一行或者同一列。
以下图为例，当我们的x=1 y=2时，行列不能重复的原则已经被红线所覆盖，那么我们现在就需要去完成（2，1），（3，1），（2，3），（3，3）这四个点的值不能和（1，2）一致。观察发现，（k，l）的值不可能与（x，y）所重复，因此得此规则。

再根据以上情况，我们算出转换后的CNF共有多少子句。
规则1：生成了 81 - 数独空缺的点（数独上已有的点）。
规则2：9 × 9 ×（1 + 2 + 3 +…8）= 2916
规则3：9 × 9 ×（1 + 2 + 3 +…8）= 2916
规则4：9 × 3 ×3 × 9 ×4 = 2916
所以，该CNF总共的变量为 9行 × 9列 ×9个可能的取值，729。子句个数为
8829 - 数独空缺的点。
根据以上规则编写代码如下。

void Sudoku2CNF(string path, int a[][9], int empty_number) {
  ofstream cnf_file;
  cnf_file.open(path, ios::out);//定义输入文件 in English: define the input file
  if (!cnf_file) {
    printf("can't open!\n");
  }
  cnf_file << "p" << " " << "cnf" << " " << 729 << " " << 8829 + 81 - empty_number << endl;
  //根据已有的数字进行子句的添加 in English: according to the sudoku problem add the number we already have.
  for (int i = 0; i < 9; ++i) {
    for (int j = 0; j < 9; ++j) {
      if (a[i][j] != 0) {
        cnf_file << (i + 1) * 100 + (j + 1) * 10 + a[i][j] << " " << 0 << endl;
      }
    }
  }
  //单个方块内只能出现1-9中的其中一个 in English: Cells must be filled in with a number between 1 and 9.
  for (int i = 1; i <= 9; ++i) {
    for (int j = 1; j <= 9; ++j) {
      for (int z = 1; z <= 9; ++z) {
        cnf_file << i * 100 + j * 10 + z << " ";
      }
      cnf_file << 0 << endl;
    }
  }
  //行不能出现重复的规则 in English: Rows can not have duplicate numbers.
  for (int z = 1; z <= 9; ++z) {
    for (int j = 1; j <= 9; ++j) {
      for (int i = 1; i <= 8; ++i) {
        for (int k = i + 1; k <= 9; ++k) {
          cnf_file << 0 - (i * 100 + j * 10 + z) << " " << 0 - (k * 100 + j * 10 + z) << " " << 0 << endl;
        }
      }
    }
  }
  //列不能出现重复的规则  in English: Columns can not have duplicate numbers.
  for (int z = 1; z <= 9; ++z) {
    for (int i = 1; i <= 9; ++i) {
      for (int j = 1; j <= 8; ++j) {
        for (int k = j + 1; k <= 9; ++k) {
          cnf_file << 0 - (i * 100 + j * 10 + z) << " " << 0 - (i * 100 + k * 10 + z) << " " << 0 << endl;
        }
      }
    }
  }
  //每个 3 ×3的小方格内不能有重复的数字  in English: Subsquares can not have duplicate numbers.
  for (int z = 1; z <= 9; ++z) {
    for (int i = 0; i <= 2; ++i) {
      for (int j = 0; j <= 2; ++j) {
        for (int x = 1; x <= 3; ++x) {
          for (int y = 1; y <= 3; ++y) {
            for (int k = 1; k <= 3; ++k) {
              for (int l = 1; l <= 3; ++l) {
                if (x == k or y == l) {
                  continue;
                } else {
                  cnf_file << 0 - (k * 100 + l * 10 + z) << " " << 0 - (x * 100 + y * 10 + z) << " " << 0 << endl;
                }
              }
            }
          }
        }
      }
    }
  }
  cnf_file.close();

}

注意点

之后我们存储的CNF 的变量个数为729个，但在CNF的子句中出现了999这样的数字，代表了9行9列其值为9.由于999 > 729。在程序的编写过程中，如果我们用正常的DPLL SAT来解决会出现越界的情况，因此需要对原有的DPLL SAT进行一些修改，将999 对应到 729， 将111 映射到 1。此处在程序实现上很简单不再过多赘述，提出这个点即可。

上述内容均在Github，如果对这个内容感兴趣，欢迎阅读。

Ⅳ、算法升级

对于CDLL其回溯只能到上一层，但有时候错误早已出现，回溯一层显得太疲软。如果算法能根据冲突来进行更高的回溯，那么SAT的运行效率回非常高。这就是CDCL（Conflict-Driven Clause Learning）算法。其命名就是根据冲突来推动的子句学习算法。算法的理解还是请看上面的华盛顿大学的那片文章，具体内容看这位博主的文章 合取范式可满足性问题：CDCL（Conflict-Driven Clause Learning）算法详解 或者这个 Conflict-driven clause learning (CDCL) SAT solvers文章来源地址https://www.toymoban.com/news/detail-694001.html

参考文献

1. Clarke, E.M., Henzinger, Th.A., Veith, H., Bloem, R. (Eds.). Handbook of Model Checking. 2018.
2. Conflict Driven Clause Learning University of Washington | CSE 442
3. Conflict-driven clause learning (CDCL) SAT solvers
4. Billy1900/DPLL-Algorithm
5. sukrutrao / SAT-Solver-DPLL
6. DPLL algorithm - Wikipedia
7. Unit propagation - Wikipedia

到了这里，关于Propositional SAT Solving：DPLL算法求解CNF SAT 与 数独求解程序(C++ 实现)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！