【每日一题Day316】LC449序列化和反序列化二叉搜索树

这篇具有很好参考价值的文章主要介绍了【每日一题Day316】LC449序列化和反序列化二叉搜索树 | BFS。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

序列化和反序列化二叉搜索树【LC449】

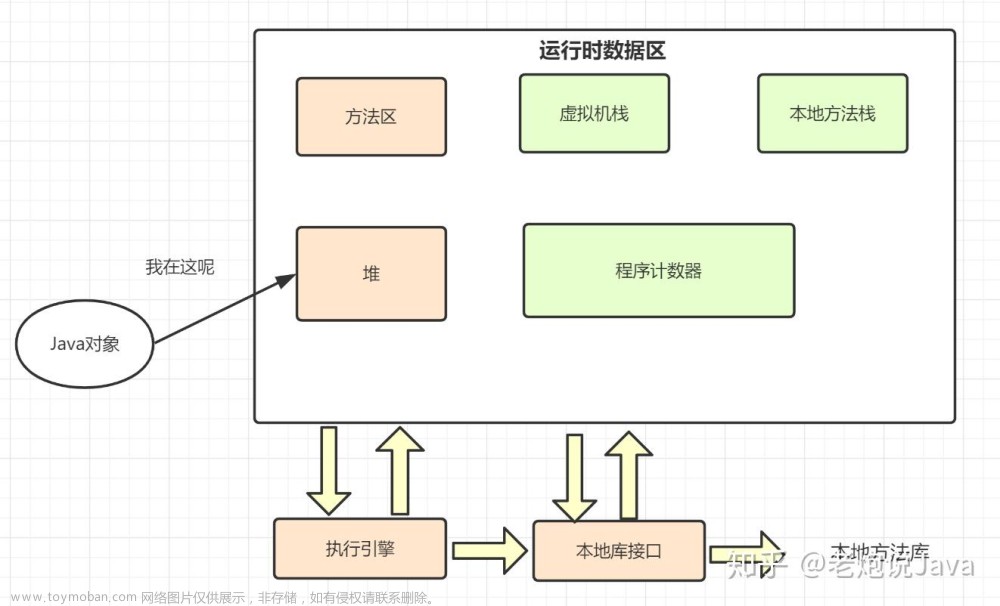
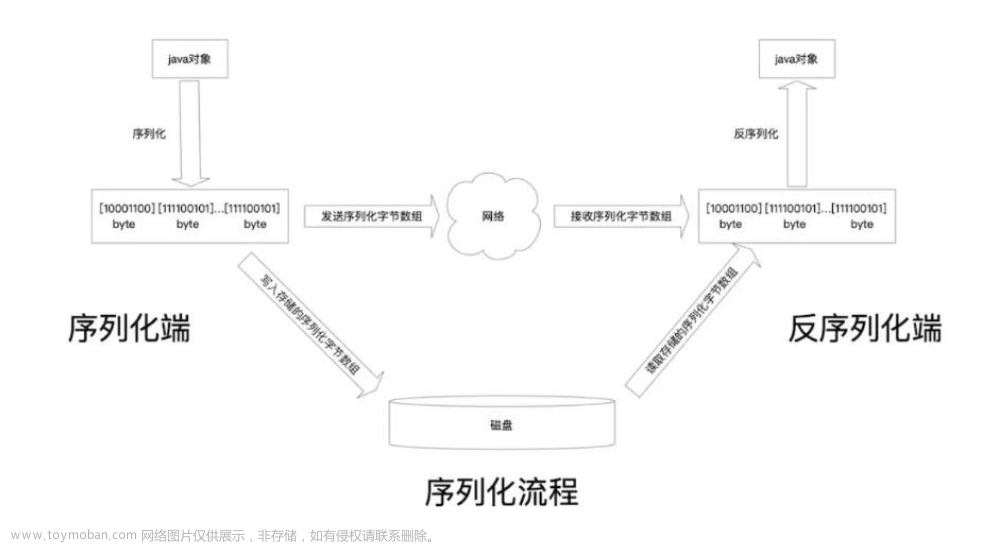
序列化是将数据结构或对象转换为一系列位的过程，以便它可以存储在文件或内存缓冲区中，或通过网络连接链路传输，以便稍后在同一个或另一个计算机环境中重建。

设计一个算法来序列化和反序列化 二叉搜索树 。对序列化/反序列化算法的工作方式没有限制。您只需确保二叉搜索树可以序列化为字符串，并且可以将该字符串反序列化为最初的二叉搜索树。

编码的字符串应尽可能紧凑。

BFS

思路
- 序列化：按照层序遍历序列化二叉搜索树，每个值以","分隔，不记录null值
- 反序列化：由于该树为二叉搜索树，满足左子树值小于根、右子树值大于根；因此对于每个节点 $i$ ，可以从根出发，找到相应的插入位置，将当前节点记为cur，插入节点值记为 $x$
  - 如果当前节点的左子节点为空，并且 $c u r . v a l > x$ ，那么插入位置为 $c u r . l e f t$
  - 如果当前节点的右子节点为空，并且 $c u r . v a l < x$ ，那么插入位置为 $c u r . r i g h t$
  - 都不满足时，选择向左或者向右遍历

实现文章来源地址https://www.toymoban.com/news/detail-694398.html

//@背书包的小白熊
public class Codec {

    // Encodes a tree to a single string.
    //java广度优先搜索层序遍历，记录所有节点的val值，用逗号隔开
    public String serialize(TreeNode root) {
        if (root == null) return "";
        Queue<TreeNode> queue = new LinkedList();
        queue.offer(root);
        StringBuilder sb = new StringBuilder();
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            sb.append(cur.val).append(",");
            if (cur.left != null) queue.offer(cur.left);
            if (cur.right != null) queue.offer(cur.right);
        }
        return sb.deleteCharAt(sb.length() - 1).toString();
    }

    // Decodes your encoded data to tree.
    //将字符串恢复成树
    public TreeNode deserialize(String data) {
        if (data.equals("")) return null;
        //将data分隔开
        String[] arr = data.split(",");
        //初始化根节点
        TreeNode root = new TreeNode(Integer.valueOf(arr[0]));
        //从第二个节点开始循环，二叉搜索树的特点是：
        //1.非空左子树的所有键值小于其根结点的键值。
        //2.非空右子树的所有键值大于其根结点的键值。
        //3.左、右子树都是二叉搜索树。
        //利用此性质，每次搜索插入节点时间复杂度为O(logn)，总体时间复杂度为O(nlogn)
        for (int i = 1; i < arr.length; i++) {
            int x = Integer.valueOf(arr[i]);
            TreeNode cur = root;
            while (cur != null) {   
                //如果左子树为空，并且x < cur.val 证明此节点就是需要插入的节点位置
                if (cur.left == null && x < cur.val) {
                    cur.left = new TreeNode(x);
                    break;
                    //如果右子树为空，并且x > cur.val 证明此节点就是需要插入的节点位置
                } else if (cur.right == null && x > cur.val) {
                    cur.right = new TreeNode(x);
                    break;
                }              
                //选择向左或向右遍历
                if (x < cur.val) cur = cur.left;
                else cur = cur.right;
            }
        }
        return root;
    }
}