【力扣】304. 二维区域和检索 - 矩阵不可变＜二维前缀和＞-Toy模板网

这篇具有很好参考价值的文章主要介绍了【力扣】304. 二维区域和检索 - 矩阵不可变＜二维前缀和＞。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【力扣】304. 二维区域和检索 - 矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和。

【力扣】304. 二维区域和检索 - 矩阵不可变＜二维前缀和＞,# 前缀和,力扣及OJ,leetcode,矩阵,算法

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
- $10^5$ <= matrix[i][j] <= $10^5$
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 $10^4$ 次 sumRegion 方法

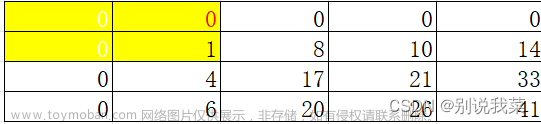
二维前缀和理论

初始化

【力扣】304. 二维区域和检索 - 矩阵不可变＜二维前缀和＞,# 前缀和,力扣及OJ,leetcode,矩阵,算法

因此二维前缀和预处理公式：

s[i][j] = s[i-1][j] + s[i][j-1] -s[i-1][j-1] + a[i][j]

计算面积

【力扣】304. 二维区域和检索 - 矩阵不可变＜二维前缀和＞,# 前缀和,力扣及OJ,leetcode,矩阵,算法

因此二维前缀和计算公式：（以（x1,y1）为左上角，（x2,y2）为右下角的子矩阵的和）

s[x2][y2] - s[x2][y1 - 1] + s[x1 - 1][y2] -s[x1 - 1][y1 - 1]

题解

都加一，数组从（0,0）开始文章来源地址https://www.toymoban.com/news/detail-694596.html

class NumMatrix {
    int[][] s;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;

        if (m > 0) {
            int n = matrix[0].length;
            s = new int[m + 1][n + 1];
            // 初始化
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    s[i + 1][j + 1] = s[i][j + 1] + s[i + 1][j] - s[i][j] + matrix[i][j];
                }
            }
        }
    }

	// 计算面积
    public int sumRegion(int x1, int y1, int x2, int y2) {
        return s[x2 + 1][y2 + 1] - s[x2 + 1][y1] - s[x1][y2 + 1]  + s[x1][y1];
    }
}