时序预测 | MATLAB实现PSO-LSSVM粒子群算法优化最小二乘支持向量机时间序列预测未来
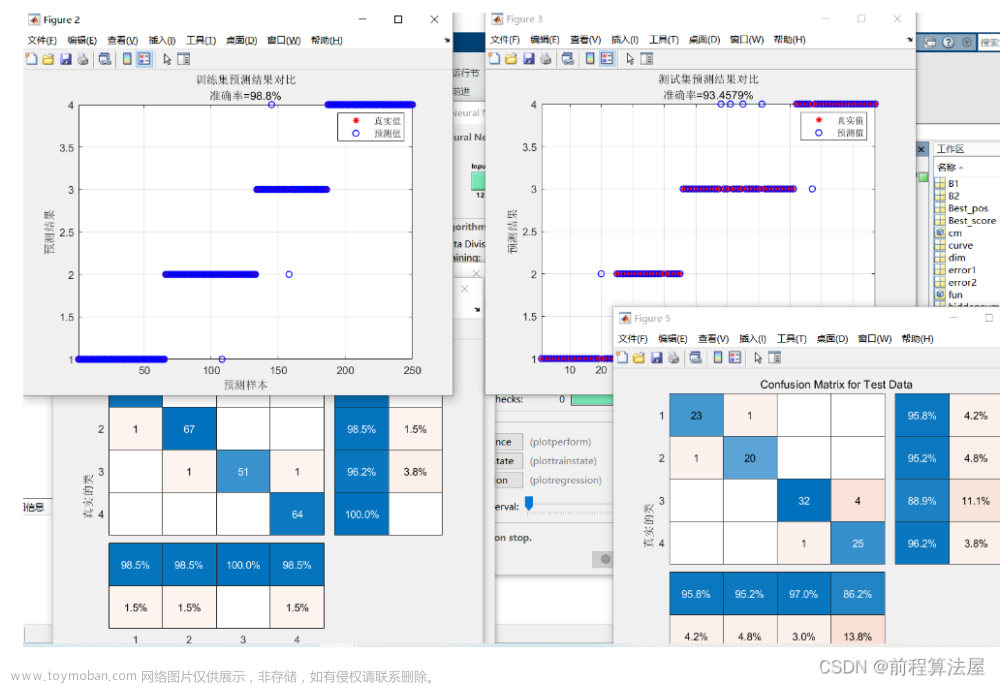
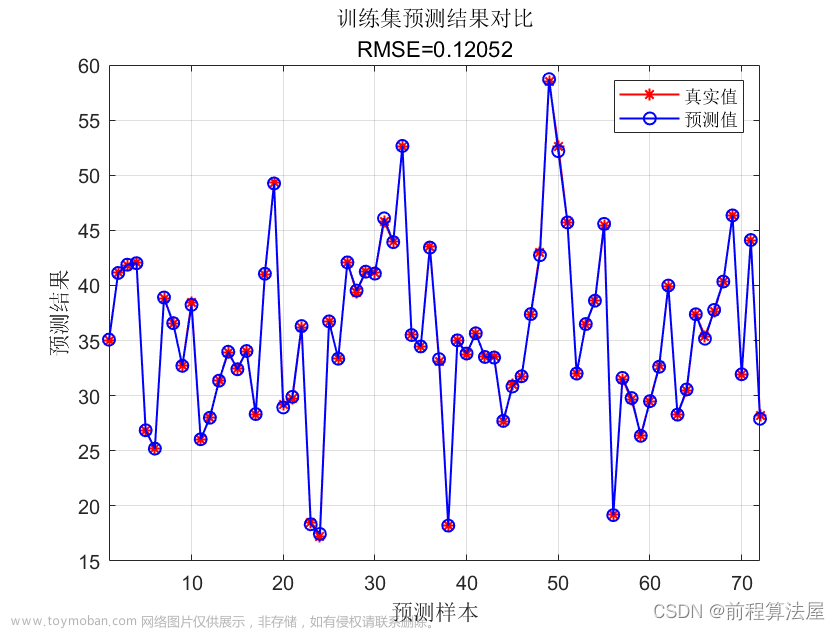
预测效果
基本介绍
1.Matlab实现PSO-LSSVM时间序列预测未来(粒子群优化最小二乘支持向量机，优化RBF核函数的gam和sig)；
2.运行环境Matlab2018及以上，data为数据集，单变量时间序列预测，运行主程序PSO_LSSVMTSF即可，其余为函数文件，无需运行；
3.递归预测未来数据，可以控制预测未来大小的数目，适合循环性、周期性数据预测；
4.命令窗口输出R2、MAE、MAPE、MBE、MSE等评价指标。
模型描述
LSSVM参数优化问题没有确定或通用的共识方法。由于智能算法在预测模型参数的选取确定方面具有稳健性和通用性，预测模型参数最优化过程中主要采用了遗传算法、果蝇优化算法、萤火虫算法、粒子群算法（ＰＳＯ）、网格搜索算法、神经网络等智能算法。粒子群算法不断调整自身和种群最优位置关系，具有更强寻优能力。因此，为进一步得到可靠的模型参数，可沿用粒子群算法进行尝试验证。
文章来源：https://www.toymoban.com/news/detail-694781.html
程序设计
- 完整程序和数据下载方式私信博主回复：MATLAB实现PSO-LSSVM粒子群算法优化最小二乘支持向量机时间序列预测未来。
%% 参数设置
pop = 5; % 种群数目
Max_iter = 50; % 迭代次数
dim = 2; % 优化参数个数
lb = [10, 10]; % 下限
ub = [1000, 1000]; % 上限
%% 优化函数
fobj = @(x)fitnessfunclssvm(x, p_train, t_train);
%% 优化
[Best_pos, Best_score, curve] = PSO(pop, Max_iter, lb, ub, dim, fobj);
%% LSSVM参数设置
type = 'f'; % 模型类型 回归
kernel = 'RBF_kernel'; % RBF 核函数
proprecess = 'preprocess'; % 是否归一化
%% 建立模型
gam = Best_score(1);
sig = Best_score(2);
model = initlssvm(p_train, t_train, type, gam, sig, kernel, proprecess);
%% 训练模型
model = trainlssvm(model);
%% 模型预测
t_sim1 = simlssvm(model, p_train);
t_sim2 = simlssvm(model, p_test);
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
%% 定义粒子群算法参数
% N 种群 T 迭代次数
%% 随机初始化种群
D=dim; %粒子维数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
w=0.8; %惯性权重
Xmax=ub; %位置最大值
Xmin=lb; %位置最小值
Vmax=ub; %速度最大值
Vmin=lb; %速度最小值
%%
%%%%%%%%%%%%%%%%初始化种群个体（限定位置和速度）%%%%%%%%%%%%%%%%
x=rand(N,D).*(Xmax-Xmin)+Xmin;
v=rand(N,D).*(Vmax-Vmin)+Vmin;
%%%%%%%%%%%%%%%%%%初始化个体最优位置和最优值%%%%%%%%%%%%%%%%%%%
p=x;
pbest=ones(N,1);
for i=1:N
pbest(i)=fobj(x(i,:));
end
%%%%%%%%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%%%%%%%%
g=ones(1,D);
gbest=inf;
for i=1:N
if(pbest(i)<gbest)
g=p(i,:);
gbest=pbest(i);
end
end
%%%%%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%%%%%%%
for i=1:T
i
for j=1:N
%%%%%%%%%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%%%%%
if (fobj(x(j,:))) <pbest(j)
p(j,:)=x(j,:);
pbest(j)=fobj(x(j,:));
end
%%%%%%%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%%%%%%%
if(pbest(j)<gbest)
g=p(j,:);
gbest=pbest(j);
end
%%%%%%%%%%%%%%%%%跟新位置和速度值%%%%%%%%%%%%%%%%%%%%%
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...
+c2*rand*(g-x(j,:));
x(j,:)=x(j,:)+v(j,:);
%%%%%%%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%%%%%%%%
if length(Vmax)==1
for ii=1:D
if (v(j,ii)>Vmax) | (v(j,ii)< Vmin)
v(j,ii)=rand * (Vmax-Vmin)+Vmin;
end
if (x(j,ii)>Xmax) | (x(j,ii)< Xmin)
x(j,ii)=rand * (Xmax-Xmin)+Xmin;
end
end
else
for ii=1:D
if (v(j,ii)>Vmax(ii)) | (v(j,ii)< Vmin(ii))
v(j,ii)=rand * (Vmax(ii)-Vmin(ii))+Vmin(ii);
end
if (x(j,ii)>Xmax(ii)) | (x(j,ii)< Xmin(ii))
x(j,ii)=rand * (Xmax(ii)-Xmin(ii))+Xmin(ii);
end
end
end
end
%%%%%%%%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%%%%%%%%%%
Convergence_curve(i)=gbest;%记录训练集的适应度值
参考资料
[1] https://blog.csdn.net/article/details/126072792?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/article/details/126044265?spm=1001.2014.3001.5502文章来源地址https://www.toymoban.com/news/detail-694781.html
到了这里，关于时序预测 | MATLAB实现PSO-LSSVM粒子群算法优化最小二乘支持向量机时间序列预测未来的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
