一.前言
在计算机科学中,排序算法是最重要的算法之一。排序算法可以将一组无序的数据按照一定的规则重新排列,使其变为有序的数据集合。排序算法的应用十分广泛,它们在计算机科学、数据结构、数据库、人工智能、机器学习等领域都扮演着重要的角色。
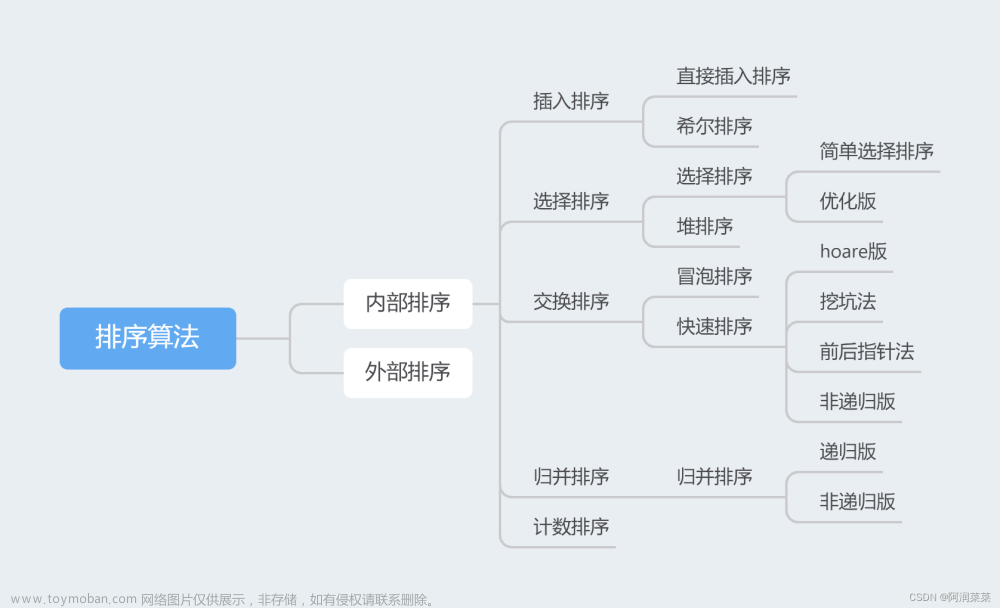
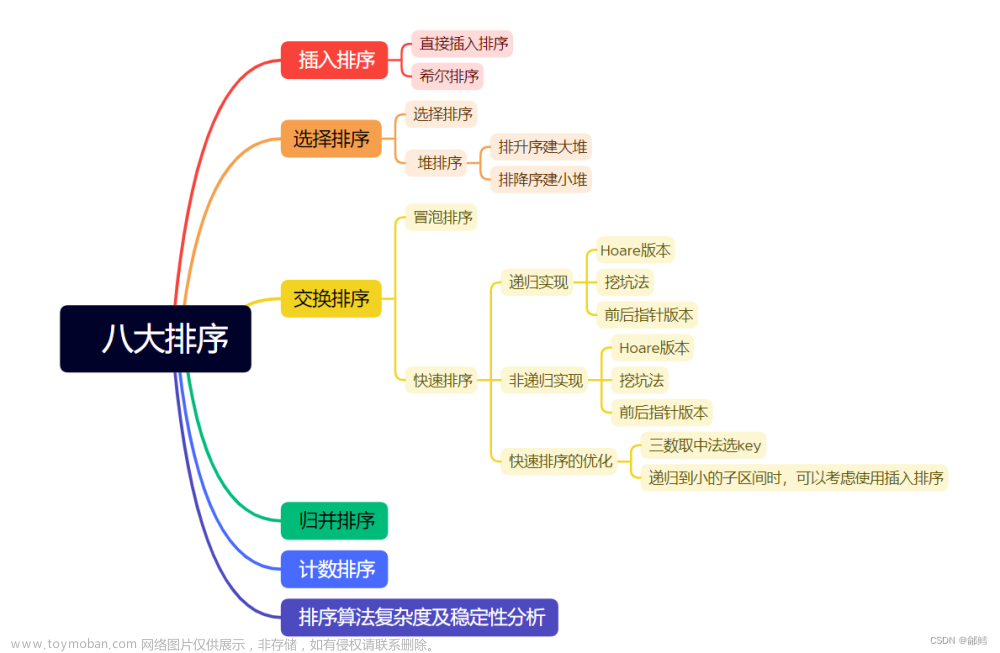
本文将介绍C++/C语言中的八大排序算法,包括冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序。这些排序算法各有优缺点,选择合适的算法可以优化程序效率,提升算法的性能。本文将对这些算法进行详细的介绍,希望读者可以通过阅读本文对排序算法有更深入的理解,同时对C++语言的使用也会有更加熟练的掌握。
二、排序的分类
插入排序:直接插入排序,希尔排序
选择排序:选择排序,堆排序
交换排序:冒泡排序,堆排序
归并排序,计数排序
三、排序实现
1.直接插入排序
(1)基本思想
将数据分为两部分,前部分为已排好数据,后一部分是待排数据,将后部分的数据逐个与前面比较大小并进行插入,直到所有的数据插入完 为止,以此得到一个有序序列。
(2)基于上述,可以设置一个end下标,以此分割两部分,[0,end]为有序序列,将end+1与[0,end]逐个进行比较,将大于end+1的数据依次往后挪动,当end+1小于某个数据或比下标0的位置的小时,就插入在该数据或下标0的位置上。
代码部分实现
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
2.希尔排序
(1)基本思想
希尔排序是基于直接插入排序的优化版,相比于前者,此算法多了一个gap用来分组,用来进行的一次排序称为预排序,使之接近有序,以下图片便是分组示例
1.gap越大,大的数可以越快到后面,小的数可以越快到前面, 但是gap越大,预排越不接近有序
2.gap越小,越接近有序,当gap为1时就是直接插入排序
通常,希尔排序的间隔首先取数组长度的一半,然后逐步减半,直到间隔为1。
这种选择间隔的方式是为了在排序过程中尽可能地减少逆序对的数量。逆序对是指在数组中,如果一个元素比它后面的元素大,那么它们就构成一个逆序对。通过选择较大的间隔,可以使得元素可以跳过一些位置直接交换,从而更快地消除逆序对。
(2)代码实现
gap可以取gap/2,也可以取gap/3+1,总之要使之能到1
void ShellSort(int* a, int n)//希尔排序
{
int gap=n;
while(gap>1)
{
gap = gap / 3+1;
for (int i = 0; i <n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
3.直接选择排序
(1)基本思想
1.首先,从待排序的序列中选择最小(或最大)的元素,将其与序列的第一个元素进行交换。
2.然后,在剩余的未排序序列中选择最小(或最大)的元素,将其与序列的第二个元素进行交换。
重复上述步骤,直到所有元素都排序完成。
(2)代码实现
void SelectSort(int* a, int n)
{
for (int i = 0; i < n- 1; i++)
{
for (int j = i + 1; j < n; j++)
{
if (a[i] > a[j])
swap(a[i],a[j]);
}
}
}
(3)代码优化
上述代码是在一次循环中只找出一个,但是可以在一次循环中找出一个最大和一个最小,放入到开头和末尾,所以就定义两个指针begin和end
(4)代码实现
特别注意要考虑到begin和mini交换时会影响到max的位置
void SelectSort2(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin; i <= end; ++i)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
swap(a[begin], a[mini]);
if (maxi == begin)//注意
{
maxi = mini;
}
swap(a[end], a[maxi]);
++begin;
--end;
}
}
4.堆排序
(1)相关概念
在了解堆排序之前应先了解如下知识点
1.堆是二叉树按层序用数组表示,堆的逻辑结构是一个完全二叉树,物理结构是一个数组
2.下标父子节点
leftchild=parent2+1;
rightchild=parent2+2;
parent=(child-1)/2;
3.大堆要求:所有父亲大于等于孩子,堆顶元素最大
小堆要求:父亲小于等于孩子 ,堆顶元素最小
(2)基本思想
构建最大堆(或最小堆):将待排序的序列构建成一个最大堆(或最小堆)。最大堆的性质是父节点的值大于等于其子节点的值,最小堆的性质是父节点的值小于等于其子节点的值。
排序:将堆顶元素与最后一个元素交换位置,然后对剩余的 n-1 个元素重新构建最大堆(或最小堆)。重复这个过程,直到所有元素都被排序。
首先先建堆
(3)建(大)堆代码实现
(注意要更新父子节点)
void AdjustDownbig(int* a, int n, int root)//左右都是大堆
{
int parent = root;
int child = parent * 2 + 1;//默认左孩子
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] >a[parent])
{
swap(a[child], a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
(4)最后代码实现
要从最后一个父节点开始建大堆
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDownbig(a, n, i);//建立堆
}
//排升序是建大堆,不是建小堆(没有效率优势,结构会全部被打乱)
//最大的数换到最后
int end = n - 1;
while (end > 0)
{
swap(a[0], a[end]);
AdjustDownbig(a, end, 0);
end--;
}
}
5.冒泡排序
(1)基本思想
1.从序列的第一个元素开始,依次比较相邻的两个元素的大小。
2.如果前一个元素大于后一个元素,就进行交换,使得较大的元素向后移动。
3.继续从第一个元素开始,重复上述比较和交换操作,直到末尾元素。
重复以上步骤,直到所有的元素都按照从小到大的顺序排列好。
(2)代码实现
void BubbleSort(int* a, int n)
{
for (int j =1; j < n; ++j)
{
int exchange = 0;
for (int i = 0; i < n-j; ++i)
{
if (a[i +1] < a[i])
{
swap(a[i +1], a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}
6.快速排序
1.挖坑法
(1)基本思路
1.选择一个key(一般选择第一个或者随机选择)作为参考。
2.从序列的右端开始,定义两个指针:begin指向左端,end指向右端。
3.不断移动指针end,直到找到一个比枢轴元素小的元素,停下来。
4.不断移动指针begin,直到找到一个比枢轴元素大的元素,停下来。
当end和begin相遇时就停止
这样比key小的就在其左边,比其大的就在其右边
(2)代码实现(完整代码在后面)
注:因为存在偶然性,所以挖坑的数采用三数取中法
三数取中法代码如下
int GetMid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
int PartSort1(int* a, int left, int right)
{
int begin = left, end = right;
int index = GetMid(a, left, right);
swap(a[begin], a[index]);
int pivot = begin;
int key = a[begin];
while (begin < end)
{
//右边找小的放到左边填坑
while (begin < end && a[end] >= key)
{
end--;
}
a[pivot] = a[end];
pivot = end;
//左边找大的放到右边填坑
while (begin < end && a[begin] <= key)
{
begin++;
}
a[pivot] = a[begin];
pivot = begin;
}
pivot = begin;
a[pivot] = key;
return pivot;
}
2.前后指针法
(1)基本思路
1.选择一个keyi(一般选择第一个或者随机选择)作为参考。
2.定义两个指针,一个指向序列的头部,称为前指针begin,另一个指向序列的尾部,称为后指针end。
3.通过移动前指针和后指针,寻找两个元素,使得前指针所指的元素大于枢轴元素,后指针所指的元素小于keyi所在的元素。
4.如果前指针所指的元素大于keyi所在的元素,并且后指针所指的元素小于keyi所在的元素,则交换这两个元素的位置。
重复步骤3和4,直到前指针和后指针相遇
(2)代码实现
nt PartSort2(int* a, int left, int right)
{
int index = GetMid(a, left, right);
swap(a[left], a[index]);
int begin = left;
int end = right;
int keyi = begin;
while (begin < end)
{
while (begin < end && a[end] >= a[keyi])
{
end--;
}
while (begin < end && a[begin] <= a[keyi])
{
begin++;
}
swap(a[begin], a[end]);
}
swap(a[begin], a[keyi]);
return begin;
}
最终代码
把枢轴元素的左右分成两个区间,再采用分治递归的方法得到最终结果
注:在分出来的区间值小于10时,可采用插入排序来提高效率
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
return;
}
int keyIndex = PartSort1(a, left, right);//可替PartSort2或PartSort3
//[left,right]
//[left,pivot-1],pivot,[pivot+1,right],分治递归
if (keyIndex - 1 - left > 10)
{
QuickSort(a, left, keyIndex - 1);
}
else
{
InsertSort(a + left, keyIndex - 1 - left + 1);
}
if (right-1- keyIndex > 10)
{
QuickSort(a, keyIndex + 1, right);
}
else
{
InsertSort(a+ keyIndex +1, right- keyIndex);
}
}
3.左右指针法
(1)基本思路
1.选择一个枢轴元素(一般选择第一个或者随机选择)作为参考。
2.定义一个左指针(prev),指向序列的最左端,定义一个右指针(cur),指向他的下一个
3.从右指针开始,向右遍历,找到比枢轴元素小的值就存到左指针所在的位置,并将两指针都往下移一位
4.最后prev所在的位置就是枢轴元素应该在的下标
(2)代码实现
int PartSort3(int* a, int left, int right)
{
int index = GetMid(a, left, right);
swap(a[left], a[index]);
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi]&&++prev!=cur)
{
swap(a[prev], a[cur]);
}
cur++;
}
swap(a[keyi], a[prev]);
return prev;
}
4.非递归实现
(1)基本思路
1.首先,因为递归调用的空间太多,导致栈溢出,内存空间分配不够的问题,所以采用模拟栈的方法
2.先用partsort先确定keyi(入栈左右区间来确定left,right然后在弹出),将其分为左右两部分区间,在对于左右两部分开始模拟
(2)代码实现
void QuickSortNonR(int* a, int left, int right)
{
stack<int> st;
st.push(right);
st.push(left);
while (!st.empty())
{
int begin = st.top();
st.pop();
int end = st.top();
st.pop();
int keyi = PartSort3(a, begin, end);
if (left < keyi-1)
{
st.push(keyi - 1);;
st.push(left);
}
if (keyi + 1 < right)
{
st.push(right);
st.push(keyi + 1);
}
}
}
7.归并排序
(1)基本思路
1.将待排序序列平均分成两个子序列,分别对两个子序列进行递归排序,直到每个子序列的长度变为1或为空。
2.将排好序的子序列按照顺序进行合并,得到一个有序的序列。
(2)具体步骤
1.创建一个临时数组,用来暂存合并后的结果。
2.找到位于中间的元素,将数组分为左右两部分
3.每一部分都定义两个指针,来指向头和尾
4.将两部分合并就是比较两数组最靠前的两个元素谁小谁先入数组(可参考合并链表)
(3)代码实现
void _MergeSort(int* a, int left, int right,int* tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right)>>1;
//[left,mid],[mid+1,right]
_MergeSort(a,left, mid,tmp);
_MergeSort(a,mid + 1,right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
for (int i = left; i <= right; ++i)
{
a[i] = tmp[i];
}
}
void MergeSort(int* a, int n)
{
int* tmp = new int[n];
_MergeSort(a, 0, n - 1, tmp);
delete[] tmp;
}
1.非递归实现
(1)基本思路
1.将待排序的序列划分成若干个长度为1的子序列。
2.创建一个与原始序列大小相同的辅助数组作为临时存储空间。
3.对于每个子序列,将相邻的两个子序列进行合并,得到一个长度为2的有序子序列。
4.按照步骤3的操作,不断迭代地对有序子序列进行两两合并,直到得到一个完全有序的序列。
5.合并的过程通过比较两个子序列的元素,并将较小的元素放入临时数组中,并移动相应的指针。
最终,将临时数组中的元素复制回原始序列的对应位置,完成排序。
(2)代码实现
void Mergesortnonr(int* a, int left, int right, int n)//归并排序非递归法
{
int* tmp = (int*)malloc(sizeof(int) * n);
int gap = 1;
while (gap < n)
{
for (int i = 0; i <= right; i = i + 2 * gap)
{
int begin1 = i, end1 = i + gap - 1, mid = i + gap - 1;
int begin2 = mid + 1, end2 = i + 2 * gap - 1;
int j = i;
if (begin2 > right) break;
if (end2 > right) end2 = right;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2]) tmp[j++] = a[begin1++];
else tmp[j++] = a[begin2++];
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
for (int j = i; j <= end2; j++)
{
a[j] = tmp[j];
}
}
gap = 2 * gap;
}
}
8.计数排序
(1)基本思想
计数排序的基本步骤如下:
1.统计每个元素出现的次数:遍历原始数组,建立一个辅助数组count,数组的索引表示元素的值,数组的值表示该元素出现的次数。初始情况下,count数组的所有值都为0。
2.累加次数:对count数组做累加操作,将当前索引位置的值与前一个索引位置的值相加,得到修改后的count数组。这个操作使得count数组的每个元素表示不大于该索引的值在原始数组中的最后一个位置。
3.排序:创建一个与原始数组大小相同的结果数组result。从原始数组的最后一个元素开始遍历,根据该元素的值,在count数组中查找对应的位置,并将这个元素放到result数组中正确的位置上。同时更新count数组中对应位置的值。
(该算法适用于元素都属于一个较小范围的整数集合时,例如排序一组学生成绩、年龄等。)
(2)代码实现
void CountSort(int* a, int n)
{
int maxi = a[0], mini = a[0];
for (int i = 0; i < n; ++i)
{
maxi = max(maxi, a[i]);
mini = min(mini, a[i]);
}
int range = maxi - mini + 1;//找出新建数组下标的范围
int* count = new int[range];
memset(count, 0, sizeof(int)*range);//重置元素值为0
for (int i = 0; i < n; ++i)
{
count[a[i] - mini]++;
}
int j = 0;
for (int i = 0; i < range; ++i)
{
while (count[i]--)
{
a[j++] = i+mini;
}
}
delete[] count;
}
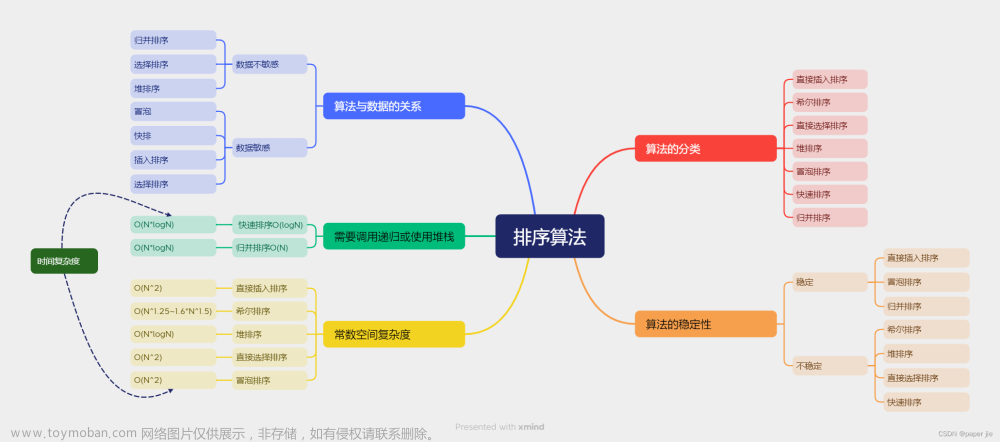
四、优劣对比及复杂度分析

1.稳定性
稳定性:指的是在排序过程中,如果两个相同元素的相对顺序在待排序的序列中已经确定,那么在排序完成后,它们的相对顺序仍然保持不变,则这个排序稳定。
1.直接插入排序:在直接插入排序中,对于相等的元素,插入操作会将后面的元素依次往后移动,为新元素腾出位置。而由于移动的是后面的元素,相等元素的相对顺序仍然保持不变,因此直接插入排序是稳定的。
2.希尔排序:在希尔排序的过程中,由于是分了很多组,所以较大的元素可能会移动到较小的元素的前面,破坏了相等元素之间的相对顺序。因此,希尔排序是一个不稳定的排序算法。
3.直接选择排序:在每一次选择最小(或最大)元素的过程中,可能会导致相等元素的相对顺序发生改变。所以不稳定。
4.堆排序:因为在此过程中会把顶元素移到最后一个去,所以会排到其相同元素后,所以不稳定
5.冒泡排序:在进行相邻元素的比较时,如果两个元素相等,我们不会进行交换,从而保持了相同元素之间的相对顺序不变。这种特性使得冒泡排序是一种稳定的排序算法。
6.快速排序:在快速排序的划分过程中,通过移动指针,找到需要交换的元素并进行交换。这个交换操作可能破坏相等元素的相对顺序,导致不稳定性。
7.归并排序:在归并排序的合并过程中,比较元素并进行合并时,如果有相等的元素,我们会先将左子序列中的元素放入结果序列,这样就保持了相等元素的相对顺序,所以稳定。
2.优劣比较
1.直接插入排序:
优点:实现简单,稳定性好,在对小规模数据或近乎有序的数据进行排序时表现良好。
(相较于冒泡和选择: 插入排序适应性比较强,再接近有序时会减少遍历)
缺点:对大规模数据排序效率相对较低。
2.希尔排序:
优点:对于中等大小的数据集合有较好的性能,相对于冒泡排序和插入排序有较高的效率。
缺点:不稳定性,实现稍复杂,需要选择合适的增量序列。
3.直接选择排序:
优点:实现简单,不占用额外的内存空间。
缺点:在大规模数据排序时性能较低,不稳定。
4.堆排序:
优点:相对于其他基于比较的排序算法,堆排序性能较高,同时也是一种不稳定的排序算法。
缺点:相对于其他算法,实现较复杂,需要了解和掌握堆的性质和操作。
5.冒泡排序:
优点:实现简单,易于理解。
缺点:效率较低,不稳定。
6.快速排序:
优点:平均情况下性能较好,实现相对简单,对大规模数据排序效率高。
缺点:在最坏情况下,时间复杂度可以达到O(n^2),是一种不稳定的排序算法。
7.归并排序:
优点:稳定的排序算法,对大规模数据排序效率较高。
缺点:实现稍复杂,需要额外的空间来存储临时数组。
8.计数排序:
优点:对于具有固定范围的整数数据排序,具有较高的性能。
缺点:只能用于整数排序,不适用于其他类型的数据;需要额外的空间来存储计数数组,当数据范围较大时,空间消耗较高。文章来源:https://www.toymoban.com/news/detail-694921.html
小白第一次写,大佬们轻点喷文章来源地址https://www.toymoban.com/news/detail-694921.html
到了这里,关于c++【数据结构】 八大排序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!