玩转线性代数(32)线性变换的相关概念的笔记,相关证明以及例子见原文
线性变换
一个将向量空间V映射到向量空间W的映射L,如果对所有的
v
1
,
v
2
∈
V
v_1,v_2\in V
v1,v2∈V及所有的标量
α
\alpha
α和
β
\beta
β,有
L
(
α
v
1
+
β
v
2
)
=
α
L
(
v
1
)
+
β
L
(
v
2
)
L(\alpha v_1+\beta v_2)=\alpha L(v_1)+\beta L(v_2)
L(αv1+βv2)=αL(v1)+βL(v2)
则称L为V到W上的一个线性变换,记为
L
:
V
→
W
L:V\rightarrow W
L:V→W
判断方法:若L为V到W上的一个线性变换,等价于:
L
(
v
1
+
v
2
)
=
L
(
v
1
)
+
L
(
v
2
)
;
L
(
λ
v
1
)
=
λ
L
(
v
1
)
L(v_1+v_2)=L(v_1)+L(v_2); L(\lambda v_1) = \lambda L(v_1)
L(v1+v2)=L(v1)+L(v2);L(λv1)=λL(v1)
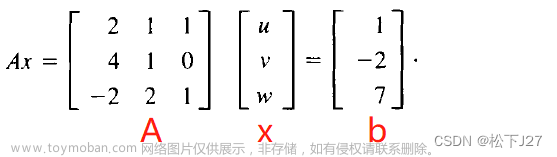
表示矩阵
对任一矩阵 A m ∗ n A_{m*n} Am∗n,可以定义一个由 R n R^n Rn到 R m R^m Rm的线性变换 L A L_A LA,称A为 L A L_A LA的表示矩阵。而每一线性变换均可由矩阵来定义,如果是 R n R^n Rn上的线性算子,则其对应矩阵为n阶方阵。
线性算子
如果V与W相同,称 L : V → V L:V\rightarrow V L:V→V为V上的一个线性算子,是一个向量空间到其自身的线性变换。
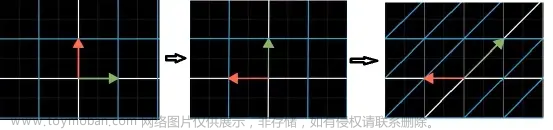
R 2 R^2 R2中特殊的线性变换
示意图见原文
旋转变换算子
A
=
(
cos
θ
−
sin
θ
sin
θ
cos
θ
)
A=\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}
A=(cosθsinθ−sinθcosθ)
绕逆时针旋转
θ
\theta
θ角
反射变换算子
B
1
=
(
1
0
0
−
1
)
B_1=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
B1=(100−1)
x轴对称
B
2
=
(
−
1
0
0
1
)
B_2=\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}
B2=(−1001)
y轴对称
投影变换算子
C
1
=
(
1
0
0
0
)
C_1=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}
C1=(1000)
只取了x坐标,所以是投影到x轴
C
2
=
(
0
0
0
1
)
C_2=\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}
C2=(0001)
只取了y坐标,所以是投影到y轴
伸压变换算子
D
1
=
(
t
0
0
1
)
D_1=\begin{pmatrix} t & 0 \\ 0 & 1 \end{pmatrix}
D1=(t001)
x坐标缩放t倍,y不变
D
2
=
(
0
0
0
t
)
D_2=\begin{pmatrix} 0 & 0 \\ 0 & t \end{pmatrix}
D2=(000t)
x坐标不变,y缩放t倍文章来源:https://www.toymoban.com/news/detail-695162.html
剪切变换算子
E
1
=
(
1
0
k
1
)
E_1=\begin{pmatrix} 1 & 0 \\ k & 1 \end{pmatrix}
E1=(1k01)
x不变,将x坐标的k倍加到y上,离y轴越远(x绝对值越大)形变越大(垂直变换)
E
2
=
(
1
k
0
1
)
E_2=\begin{pmatrix} 1 & k \\ 0 & 1 \end{pmatrix}
E2=(10k1)
y不变,将y坐标的k倍加到x上,离x轴越远(y绝对值越大)形变越大(水平变换)文章来源地址https://www.toymoban.com/news/detail-695162.html
到了这里,关于第六章,线性变换,1-线性变换、表示矩阵、线性算子的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!